Ⅰ. 서 론
모노펄스 레이더 시스템은 정밀한 각도 측정을 통해 표적의 위치를 정확하게 추정하는 데 필수적인 기술이다. 그러나 레이더 시스템은 주변 환경 변화, 자체적인 열 발생, 부품 노후화 등 다양한 요인에 의해 시간 경과에 따른 드리프트(drift) 현상이 발생할 수 있다. 이러한 드리프트는 각도 측정의 정확도를 저하시켜 시스템의 전반적인 성능에 부정적인 영향을 미친다. 따라서 장기간 운용에도 고정밀도를 유지하기 위해서는 실시간으로 드리프트를 보정하는 기법이 필수적이다.
기존의 사전 보정(pre-conditioning) 방식은 운용 전 한 차례 보정을 수행하는 방식이다. 이 방법은 초기 성능을 확보하는 데 유용하지만, 운용 중 발생하는 동적인 드리프트 변화에 대응하기 어렵다는 한계를 가진다. 외부 참조원(예: 전파 무향실, 외부 측정 장비)을 이용한 실시간 보정 방식은 높은 정확도를 제공할 수 있지만, 복잡한 인프라와 비용이 수반되며, 모든 운용 환경에서 적용하기 어렵다는 단점이 있다.
본 논문에서는 이러한 기존 방식의 한계를 극복하기 위해, 레이더 자체 송수신 신호의 일부를 활용하여 실시간으로 드리프트를 보정하는 통계 가중 기반의 버스트 보정(burst calibration) 방법을 제안한다. 제안하는 방법은 정기적인 짧은 신호 버스트를 통해 측정된 오차 샘플에 대해 다음과 같은 통계적 처리 기법을 적용한다. 첫째, 스파이크(spike)와 같은 이상치(outlier)를 효과적으로 제거하기 위해 절사 평균(trimmed mean)을 사용한다. 둘째, 보정값의 과도한 변화를 억제하여 시스템의 안정성을 확보하기 위해 클리핑(clipping) 기법을 적용한다. 마지막으로, 적절한 보정 반영 비율(α)을 통해 드리프트 추적 성능과 보정 안정성 간의 균형을 이룬다.
제안하는 기법은 별도의 외부 참조 없이 레이더 자체의 측정 데이터를 활용하므로, 경제적이고 유연하게 다양한 운용 환경에 적용될 수 있다. 또한, 실시간으로 드리프트를 추적하고 보정함으로써 모노펄스 레이더 시스템의 장기간 고정밀 각도 측정 성능을 보장할 수 있다. 본 논문에서는 다양한 시뮬레이션 환경에서 제안 기법의 성능을 정량적으로 평가하고, 기존 방식과의 비교를 통해 그 유효성을 입증한다.
Ⅱ. 관련 연구
본 장에서는 모노펄스 레이더의 각도 추정 성능 보정을 위한 기존 연구를 유형별로 분석하고, 각 기법의 특징과 한계를 살펴본다. 이는 본 논문에서 제안하는 기법의 차별성과 필요성을 부각시키는 기초가 된다. 기존 보정 기법들은 크게 사전 보정, 외부 참조 기반 실시간 보정, 그리고 내부 신호 기반 실시간 보정 방식으로 분류할 수 있다.
사전 보정은 레이더 시스템 운용 전 통제된 환경에서 수행되는 초기 보정 방식이다. 정밀 기준 시설(예: 무반사 챔버)이나 알려진 참조 표적을 이용하여 시스템의 고유 오차를 줄이고 기준 성능을 확보한다. 이 방법은 높은 초기 보정 정확도를 제공하나, 대규모 시설 및 전문 인력 필요, 그리고 운용 중에 발생하는 시스템의 동적인 드리프트에 실시간으로 대응하기 어렵다는 근본적인 한계를 가진다.
사전 보정의 한계를 극복하기 위해 외부 시스템의 도움을 받아 실시간에 가깝게 보정값을 갱신하는 방식이다. 외부 레이더, 비콘 또는 GNSS(global navigation satellite system) 수신기를 활용하여 알려진 신호원과의 각도 차이를 측정하고 보정값으로 사용한다. 이 방법은 실시간성을 확보할 수 있지만, 외부 시스템에 대한 높은 의존성으로 인해 운용 유연성이 저하되고 외부 시스템의 신뢰성에 따라 보정 성능이 좌우된다는 문제점을 야기한다.
외부 시스템 의존성 및 사전 보정의 한계를 극복하고자 레이더 자체 역량을 활용하는 방식이다. 운용 중 획득된 실제 표적 데이터를 활용하거나, 레이더 내부에 테스트 신호 또는 파일럿 시퀀스를 삽입하여 시스템 상태를 측정하고 보정값을 갱신한다. 이 방법은 외부 참조 없이 실시간 보정이 가능하나, 하드웨어 복잡도 증가, 실제 탐지 효율 저하를 야기하는 탐지 손실 가능성, 그리고 잡음에 대한 민감도 증가와 같은 한계점들을 내포하고 있다.
본 논문에서 제안하는 통계 가중 기반 burst calibration 기법은 앞서 언급된 기존 연구의 한계를 효과적으로 극복하는 새로운 접근 방식을 제시한다.
보정용 파일럿 버스트 신호는 그림 1에 도시된 바와 같이 레이더 자체 송신 신호의 일부를 내부 경로를 통해 주기적으로 송수신하는 방식으로 획득된다. 이 신호는 외부 환경이나 표적 반사에는 영향을 받지 않으므로 항상 안정적인 기준을 제공한다.
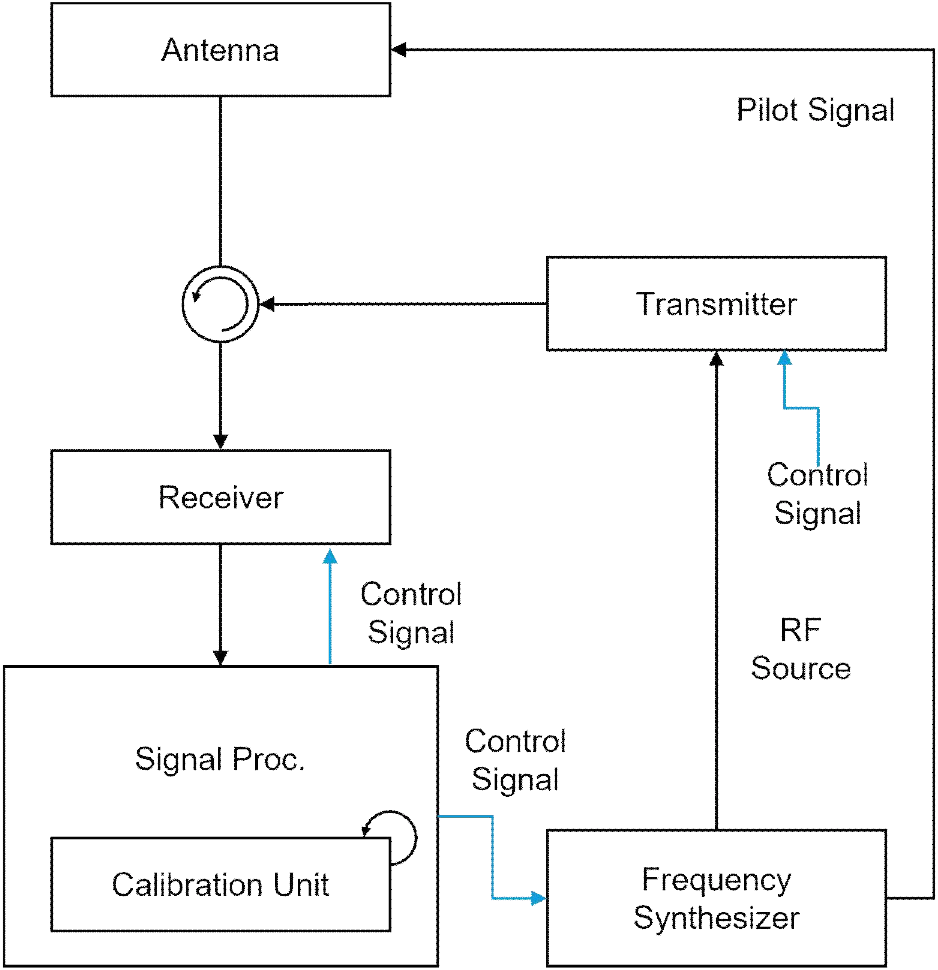
동시에 보정 대상 RF/IF 체인을 동일하게 통과하므로 체인의 드리프트 영향은 그대로 반영되며, 이에 따라 측정 잔차에는 드리프트 성분이 포함된다.
또한 그림 2에 나타난 바와 같이, 이 파일럿 버스트는 탐지 프레임 내에 주기적으로 삽입되어 실시간 보정을 가능하게 한다.
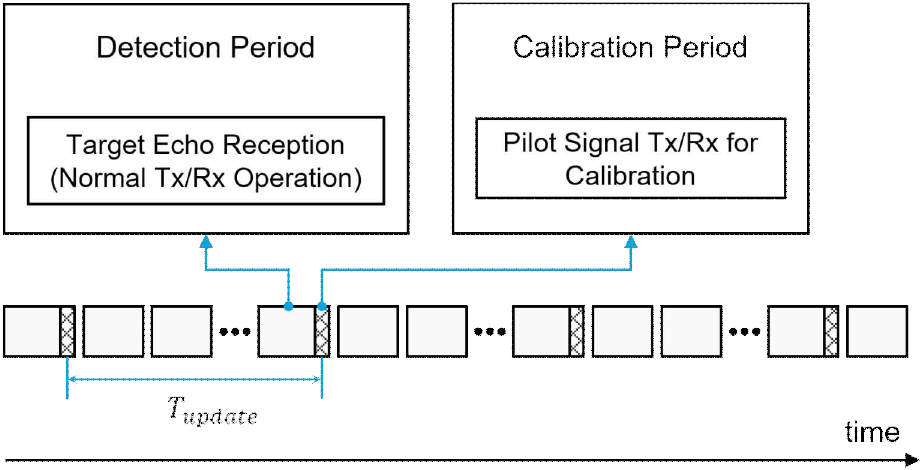
이러한 구조적 특징은 다음과 같은 장점을 가진다.
첫째, 외부 참조나 대규모 하드웨어 변경이 불필요하여 레이더 자체 송신 신호 일부를 활용함으로써 시스템 의존성과 하드웨어 복잡도를 최소화할 수 있다.
둘째, 탐지 프레임마다 짧은 버스트 구간을 주기적으로 삽입하여 전체 탐지 구간 손실을 최소화한다. 또한 trimmed mean, adaptive weighting, update clipping 등 통계적 안정화 기법을 적용함으로써 적은 샘플 수에서도 이상치와 잡음의 영향을 억제하고 신뢰성 있는 잔차 추정값을 얻을 수 있다.
셋째, 이렇게 추정된 잔차를 기반으로 보정값을 주기적으로 갱신함으로써 드리프트를 지속적으로 추적하고, 응답성과 보정값 안정성이라는 두 성능 지표를 균형 있게 확보할 수 있다.
Ⅲ. 제안 기법(Proposed Method)
본 장에서는 모노펄스 레이더의 고정밀 각도 측정 성능을 장기간 안정적으로 유지하기 위한 통계 가중 기반의 burst calibration 방법을 제안한다. 제안 기법은 레이더 자체 송신 신호의 일부를 활용한 보정용 파일럿 버스트를 통해 실시간으로 드리프트를 보정하며, 드리프트 오차 추정의 신뢰도를 높이기 위한 통계적 처리 과정을 포함한다.
본 논문에서 제안하는 보정 시스템은 그림 1과 같은 일반적인 파일럿 신호 기반 모노펄스 레이더의 시스템 구조를 따른다.
이 시스템은 그림 2에 나타난 바와 같이 대부분의 시간 동안 표적을 탐지하는 탐지 구간(detection period)으로 동작하며, 그사이에 매우 짧은 보정 구간(calibration period)을 삽입하여 보정용 파일럿 버스트를 주기적으로 송수신한다. 이 짧은 보정 구간에서 획득한 신호는 그림 3에 도시된 제안 기법의 전체 신호처리 블록 다이어그램을 따라 처리되며, 이를 통해 모노펄스 레이더의 위상 중심(phase center) 또는 안테나 패턴의 대칭성을 활용하여 측정 오차(measurement error)를 산출한다.
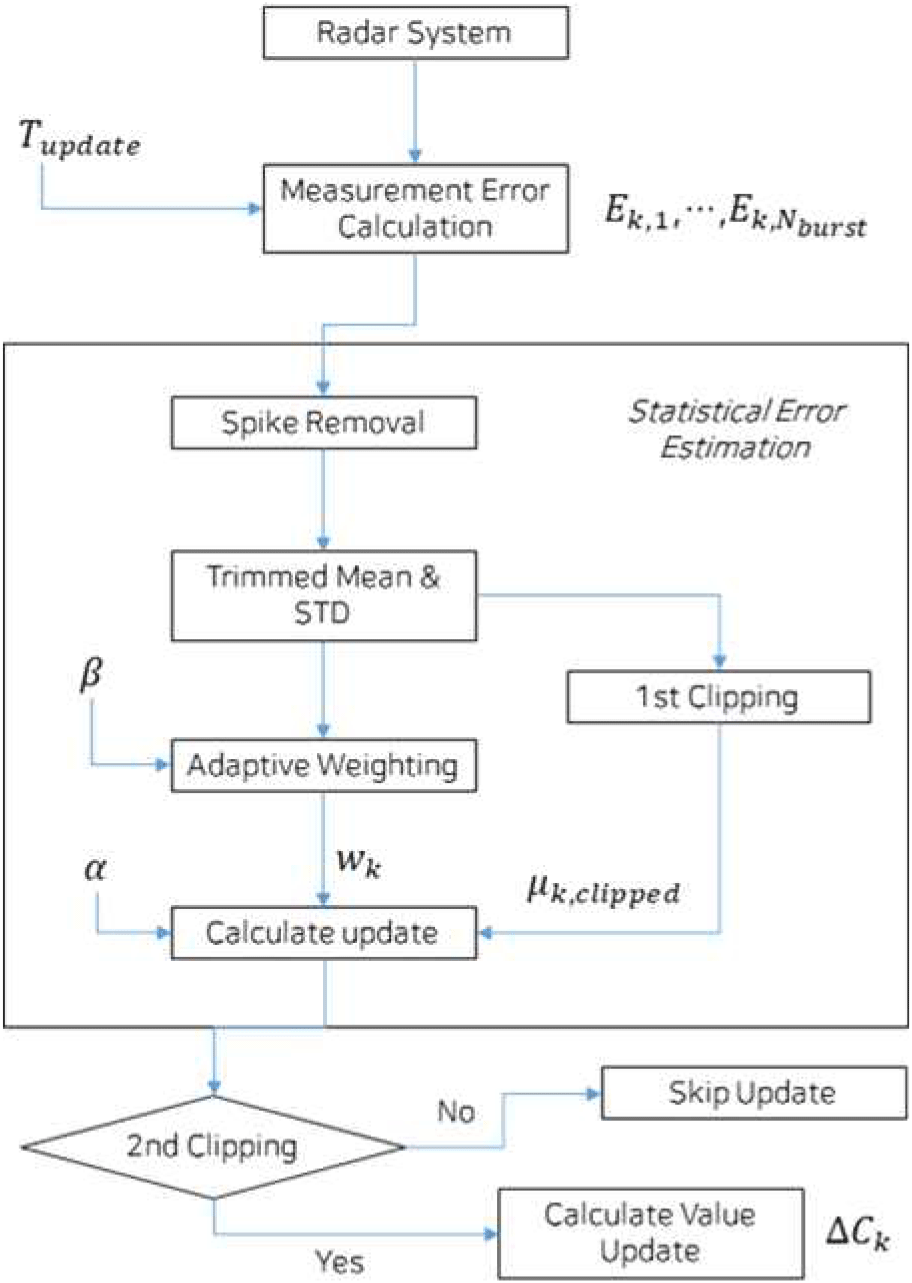
보정 주기 k에서 버스트 구간 동안 Nburst개의 샘플을 수집한다. 측정 오차(Ek,i)는 현재 측정된 각도와 이상적인 기준 각도 간의 차이를 나타내며, 이는 주로 시스템 드리프트(Dk)와 측정 노이즈(Nk,i)의 합으로 모델링될 수 있다. 즉,
여기서 Dk는 주기 k에서의 느린 드리프트(준정상)이며, Nk,i는 시스템에 따라 정의가 달라질 수 있지만 가우시안 잡음과 드문 스파이크성 교란을 포함하는 측정 잡음 등이다. 버스트 내 샘플 간격(Δtburst)은 드리프트 시정수(τdrift)에 비해 충분히 작으므로, 한 버스트 동안의 드리프트 변화는 무시할 수 있다.
또한 본 연구에서는 보정 신호로 외부 표적 산란 신호가 아니라, 레이더 시스템 내부에서 발생시키는 파일럿/테스트 신호를 사용한다. 이는 외부 환경 변화나 표적 존재 여부에 무관하게 안정적으로 보정값을 추정할 수 있도록 하기 위함이다.
목표는 측정 오차 Ek,i를 통해 드리프트 Dk를 정확하게 추정하고 보정값 Ck를 갱신하여 잔차 오차(Dk−Ck)를 최소화하는 것이다.
제안 기법의 보정값 갱신 구조는 다음 식 (2)과 같다.
여기서 Ck는 현재 보정값, ΔCk는 갱신량이며, ΔCk는 주기적으로 수집된 Nburst개의 오차 샘플()로부터 통계적으로 처리된 평균 오차 μk와 보정 반영 비율 α, 그리고 적응적 가중치 wk를 기반으로 결정된다.
여기서 TrimmedMean()은 상·하위 일부 이상치를 제거한 후 평균을 계산하는 함수이며, TrimmedSTD()는 동일한 방식으로 이상치를 제거한 후 분산을 계산한다. 또한 wk는 잡음 분산 σk와 파라미터 β에 의해 결정되는 가중치로, 잡음이 클수록 보정 반영률을 줄이도록 설계된다. 각 함수의 상세 동작은 3-2-1절 및 3-2-2 절에서 설명한다.
최종 갱신량 ΔCk는 다음의 단계를 통해 결정된다. 먼저, 절사 평균 μk에 첫 번째 클리핑을 적용하여 μk,clipped를 얻는다.
여기서 Clip()함수는 입력값을 미리 정의된 범위(±Δ1)로 제한하여 이상치에 의한 과도한 보정량을 방지한다. 이후, μk,clipped에 적용 가중치 wk와 보정 반영 비율 α를 곱하여 갱신 후보값(update candidate)을 계산한 뒤, 두 번째 클리핑 과정을 통해 최종 갱신량을 얻는다.
여기서 두 번째 Clip()은 업데이트 크기를 ±Δ2 범위로 제한하여 안정성을 확보한다. 각 Clip() 단계의 의미와 수치는 3-2-3절에서 상세히 설명한다.
따라서 최종 갱신량 ΔCk는 식 (7)과 같이 정의되며, 이 값이 보정값 Ck+1에 반영된다.
본 연구에서 제안하는 보정 기법은 모든 오차 요소를 완벽히 제거하는데 한계가 있다. 구체적으로, 드리프트(시간 경과에 따른 체계적 바이어스)나 저주파 성분의 측정 노이즈와 같이 통계적 평균화가 가능한 성분은 본 기법을 통해 효과적으로 추적·보정이 가능하다. 반면, 안테나의 구조적 비대칭, 외부 환경에서 기인하는 다중경로(multipath) 간섭, 또는 비선형 하드웨어 동작에 의해 발생하는 고차 왜곡 등은 본 연구의 접근으로 직접 보정하기 어렵다. 따라서 본 논문은 보정 가능한 오차(드리프트 및 평균화 가능한 잡음)에 초점을 두며, 보정 불가능한 오차는 별도의 시스템 설계 및 보완 절차가 필요함을 명확히 한다.
측정 오차 샘플에는 드리프트뿐만 아니라 다양한 형태의 노이즈, 특히 스파이크 노이즈와 같은 이상치(outlier)가 포함될 수 있다. 이러한 이상치는 보정값 추정의 정확도를 크게 저해할 수 있으므로, 제안 기법에서는 이를 효과적으로 처리하기 위한 통계적 방법을 적용한다.
수집된 Nburst개의 오차 샘플(Ek,j) 중 스파이크 노이즈와 같은 이상치를 효과적으로 제거하기 위해, 먼저 특정 임계값(Tspike)을 벗어나는 샘플을 필터링한다. 여기서 임계값은 Tspike=γσnoise (γ>0)로 두며, 시뮬레이션에서는 측정 노이즈 표준편차(σnoise)의 10배를 초과하는 샘플을 스파이크로 간주하여 제거하였다.
필터링된 샘플에 대해 절사 평균(trimmed mean)을 계산한다. 절사 평균은 데이터를 정렬한 후 상위 및 하위 일정 비율의 데이터를 제거하고 나머지 데이터의 평균을 계산하는 방법이다. 이는 이상치의 영향을 최소화하여 평균 추정의 강인성(robustness)을 높인다[7]. 본 시뮬레이션에서는 필터링된 샘플의 상위 및 하위 10%를 제거한 후 절사 평균을 계산하였다.
적응적 가중치(adaptive weighting)는 추정된 보정 오차의 신뢰도에 따라 보정값 갱신 반영 비율을 동적으로 조절하는 기법이다[8]. 식 (4)에서 계산된 샘플들의 표준편차 σk는 현재 보정 주기 동안 획득된 Nburst개 샘플 Ek,i들의 분산 정도를 나타낸다. 표준편차가 작다는 것은 샘플들이 서로 유사하고 평균 주위에 밀집되어 있다는 의미로, 이는 추정된 μk가 높은 신뢰도를 가진다는 것을 시사한다.
식 (5)의 가중치 함수 는 이러한 신뢰도를 정량화한다. σk→0 (매우 높은 신뢰도)일 때 wk→1이 되어, 추정된 μk가 거의 그대로 α와 곱해져 보정값 갱신에 크게 반영된다. 반대로 σk→∞(매우 낮은 신뢰도)일 때 wk→0이 되어, 추정된 μk가 보정값 갱신에 거의 반영되지 않도록 하여 불안정한 업데이트를 방지한다. 여기서 β는 측정된 잡음 분산 σk와 결합되어 업데이트 이득을 조정하는 파라미터이며, 본 논문에서는 안정성과 수렴 속도의 균형을 고려하여 β=0.2를 적용하였다.
보정값 갱신 시 과도한 변화를 억제하여 시스템의 안정성을 확보하고, 급격한 노이즈나 일시적인 이상치로 인한 오보정(over-correction)을 방지하기 위해 갱신량에 이중 클리핑(dual clipping)을 적용한다.
첫 번째 클리핑은 절사 평균으로 추정된 오차 μk 자체의 비정상적인 크기를 제한한다. 시뮬레이션에서는 ±0.2(Δ1)의 클리핑을 적용하였다. 이 임계값은 시스템이 단일 보정 주기 동안 허용할 수 있는 드리프트의 최대 예상 변화량 또는 잔류 노이즈의 통계적 상한을 고려하여 설정되었다.
두 번째 클리핑은 보정 반영 비율 α와 wk가 곱해진 최종 갱신량 update에 대해 적용된다. 시뮬레이션에서는 계산된 갱신량 |ΔCk|이 ≤0.05(Δ2)일 때만 최종 보정값 Ck+1에 더해지도록 제한한다. 이 임계값은 시스템이 보정값에 부드럽고 점진적으로 수렴하도록 유도하며, 과도한 갱신으로 인한 오버슈트를 방지하고, 미처 제거되지 못한 큰 노이즈의 영향을 차단하여 시스템의 안정성을 극대화하기 위해 설정되었다[7],[8].
보정 주기(Tupdate): 보정 주기는 보정값을 갱신하는 빈도를 결정한다. 주기가 짧을수록 드리프트 변화에 대한 응답성이 빨라지지만, 시스템의 부하가 증가하고 보정용 버스트 구간의 누적 비율이 높아질 수 있다. 반대로 주기가 길어지면 시스템 부하는 줄어들지만, 드리프트 추적이 지연되어 오차가 누적될 수 있다. 드리프트의 예상 변화 속도와 시스템 자원 가용성을 고려하여 적절한 주기를 선택한다. 본 논문에서는 기본적으로 100 ms 주기를 사용하였으며, 시뮬레이션에서는 1초에서 60초 범위의 주기를 추가적으로 고려하여 보정 성능의 변화를 분석하였다.
제안 기법은 보정용 버스트 구간 삽입을 통해 탐지 간섭을 발생시킬 수 있다. 이를 최소화하기 위해 전체 운용 프레임 대비 1~10 % 내의 보정용 구간 비율을 유지하는 것이 권장된다. 이 비율은 실제 탐지 성능과 실시간 보정 성능 간의 균형점을 설정하는 데 핵심적인 역할을 한다. 예를 들어, 프레임 내에서 탐지 펄스와 보정 펄스의 스케줄링 전략을 최적화하여 겹침을 최소화하고, 보정 펄스의 에너지를 효율적으로 활용하는 방안을 추가적으로 고려할 수 있다.
앞 절(3-2-1~3-2-4)에서 제안 기법의 동작과 운용 고려사항을 설명하였다. 본 절에서는 주요 파라미터들의 성격과 설정 근거를 종합적으로 정리하였으며, 그 결과는 표 1에 요약되어 있다.
| Parameter | Category | Basis/description |
|---|---|---|
| Nburst | System | |
| Tupdate | System | |
| r | Derived Value | |
| α | Simulation (Ref. theory) | |
| β | Simulation (Ref. theory) |
|
| δ1, δ2 | Simulation (Ref. theory) | |
| Trimming ratio | Theory (simulation-verified) |
|
| γ | Simulation (Env. condition) |
표 1은 제안 기법에서 사용된 파라미터들을 시스템, 파생, 시뮬레이션, 이론 등으로 구분하고, 각각의 설정 근거를 제시한다. 이를 통해 본 연구의 파라미터들이 단순한 경험적 조정이 아니라, 시스템 요구와 이론적 근거, 시뮬레이션 검증을 통해 합리적으로 정의되었음을 확인할 수 있다.
Ⅳ. 시뮬레이션 및 결과(Simulation and Results)
본 장에서는 제안된 통계 기반 버스트 보정 기법의 성능을 다양한 운용 조건에서 정량적으로 평가한다. 이를 위해 시뮬레이션 환경을 설정하고, 보정 반영 비율α, 샘플 수(Nburst), 보정 주기(Tupdate) 등의 주요 변수에 따라 성능을 분석하였다. 또한 초기 보정만 수행하고 실시간 업데이트를 적용하지 않은 경우와 비교함으로써, 제안 기법의 실효성을 검증하였다.
시뮬레이션은 모노펄스 레이더 시스템의 드리프트 및 측정 노이즈 특성을 반영하기 위해 다음과 같이 모델링되었다.
드리프트 D(t)는 선형, 새츄레이션(saturation), 가속(acceleration) 요소를 포함하는 비선형 함수로 모델링되었다. 이는 실제 열환경 변화에 따른 드리프트 특성을 모사한다.
여기서 Ndrift(t)는 표준편차 σdrift를 갖는 가우시안 잡음이다. 주요 파라미터는 다음과 같다: 선형 기울기 k=0.0003°/s, 새츄레이션 영향 A=0.08°, 새츄레이션 지수 감쇠율 λ1=0.015, 가속 영향 B=0.3e−10, 가속 지수 증가율 λ2=0.015, 가속 비선형성 지수 n=2.5. 드리프트 코어에 추가되는 드리프트 노이즈의 표준편차 σdrift=0.0001°.
식 (8)의 각 항은 레이더 하드웨어 운용 환경에서 관찰되는 드리프트 특성을 반영한다.
선형항 k·t은 장기간 운용 시 발생하는 지속적 바이어스를 나타내며, 포화항 은 초기 구동 시 열 평형 과정에서 나타나는 안정화 특성을 모사한다. 또한 항은 열적 안정성이 충분히 확보되지 못하거나 누적된 열과 외부 환경 요인에 의해 드리프트 속도가 비선형적으로 가속되는 현상을 반영한다. 마지막으로 Ndrift(t)는 무작위적 열 잡음을 가우시안 분포로 모델링하여 현실성을 높였다. 이와 같은 모델링은 기존 레이더 성능 모델링 문헌[9],[10]에서 제시된 선형 및 포화 개념을 기반으로 하며, 본 연구에서는 실제 운용 환경을 모사하기 위해 비선형 가속 항을 추가적으로 통합하였다.
측정 노이즈는 가우시안 노이즈에 스파이크(spike) 노이즈가 추가된 형태로 모델링되었다.
주요 파라미터는 다음과 같다: 측정 노이즈 표준편차 σnoise=0.01°, 스파이크 발생 확률 spikeprob=0.01(1 %), 스파이크 크기 spikemag=0.5.
보정 주기(Tupdate): 본 논문에서는 100 ms 주기를 기본으로 보정을 수행하였다. 다만 성능 변화를 분석하기 위해 1, 10, 30, 60초 주기도 추가적으로 고려하였다.
각 보정 주기마다 Nburst개의 샘플을 수집하며(기본 100개, 경우에 따라 50 또는 200으로 변화시켜 평가), 여기서 Nburst는 단순한 샘플 개수를 의미할 뿐 아니라, 보정 구간이 전체 탐지 프레임에서 차지하는 비율을 반영한다.
값이 클수록 추정 신뢰도는 향상되지만 탐지 손실이 증가하고, 값이 작으면 탐지 손실은 줄어드나 잡음에 대한 민감도가 커진다. 또한 버스트 내 샘플 간 간격은 수 μs 수준으로, 이는 드리프트 시정수(수 초 내지 수백 초)에 비해 충분히 작아 한 버스트 동안의 드리프트 변화는 무시할 수 있다.
제안하는 보정 기법의 성능은 장기적인 안정성과 단기적인 변동성을 모두 고려하여 평가되어야 한다. 이를 위해 본 논문에서는 RMS(root mean square)와 STD(standard deviation)를 합산한 종합 점수(score)를 성능 지표로 정의하였다.
RMS는 전체 오차의 크기를 나타내며, 특히 시간이 지남에 따라 누적되는 장기적 오프셋(offset)이나 편향(bias)과 같은 체계적 오차를 평가하는 데 효과적이다.
반면, STD는 측정값들의 산포도를 나타내며, 단기적인 랜덤 노이즈나 순간적인 변동성에 의해 발생하는 불안정성을 평가하는 데 적합하다.
즉, RMS만 사용할 경우 순간적인 안정성 평가가 어렵고, STD만 사용할 경우 장기적인 드리프트 누적을 반영할 수 없으므로 단일 지표만으로는 성능을 온전히 평가하기 어렵다. 이에 따라 RMS와 STD를 단순 합산한 score는 장기적 드리프트 추세(RMS)와 단기적 변동성(STD)을 모두 반영하는 통합 지표로 기능한다.
이러한 접근은 정밀 측정 시스템에서 오차의 편향과 분산을 동시에 고려하는 개념과 맥락을 같이하며, 이는 Kalman 필터 이론을 비롯한 기존 추정 이론에서도 그 중요성이 확인된다[11].
보정용 구간 비율 r의 증가는 유효 탐지 펄스 수 감소를 초래하며, 이는 신호대잡음비(SNR)의 저하로 이어져 결과적으로 탐지확률(Pd)에도 영향을 준다. 따라서 본 연구에서는 레이더 방정식 및 펄스 집적 가정을 바탕으로, 보정 구간 비율 변화에 따른 유효 펄스 수(Neff), SNR, 최대 탐지거리(Rmax) 변화를 시뮬레이션하였다.
보정 구간 비율 r의 증가는 유효 탐지 펄스 수 Neff의 감소로 이어지며, 이는 다음과 같은 레이더 방정식에 의해 최종 SNR과 최대 탐지 거리에 영향을 미친다.
본 시뮬레이션에서는 보정 구간 삽입이 없는 경우를 기준으로 SNR0=20 dB, Rmax,0=20 km으로 가정하였다. 그림 4에서 제시된 바와 같이, 보정 구간 비율의 증가에 따라 SNR과 최대 탐지거리가 감소하는 것을 확인할 수 있다. 예를 들어, r=0.1에서는 SNR이 약 −0.46 dB 감소하고 탐지거리가 약 3.6% 줄어든다. r=0.3에서는 −1.55 dB, 약 9.9 % 감소, r=0.5에서는 −3.01 dB, 약 15.9 % 감소한다. 이는 보정 구간 삽입으로 인해 유효 탐지 펄스 수가 줄어들기 때문이며, 결과적으로 탐지 성능 저하로 이어진다.
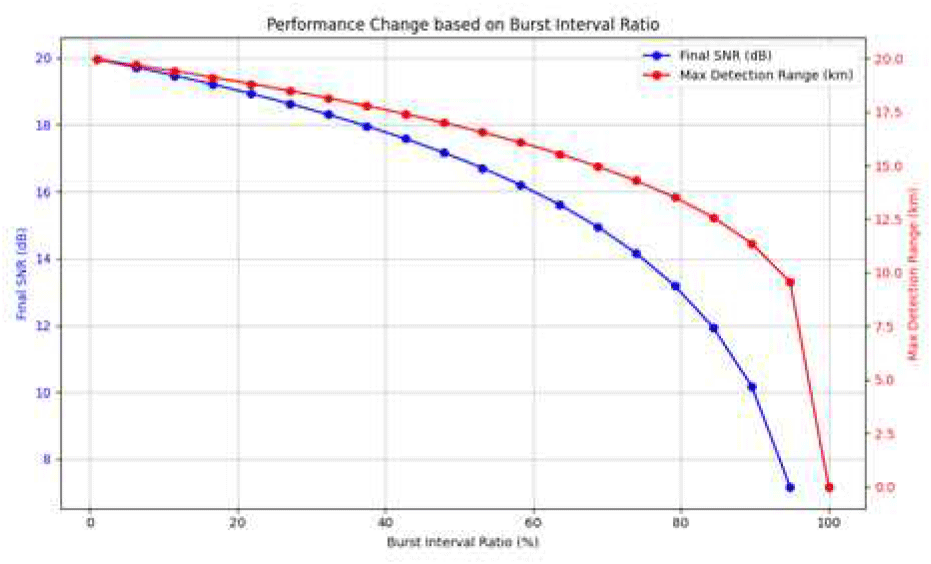
다만 본 시뮬레이션은 매 프레임마다 보정 구간을 삽입하는 worst-case를 가정한 결과이다. 실제 운용에서는 그림 2와 같이 보정 구간이 Tupdate 간격으로만 주기적으로 삽입되므로, 탐지 성능 저하는 여기서 제시된 이론치보다 작을 것으로 예상되며, 제안 기법은 드리프트 억제를 통해 시스템의 안정성을 확보하면서도 탐지 성능 손실이 미미함을 보여준다.
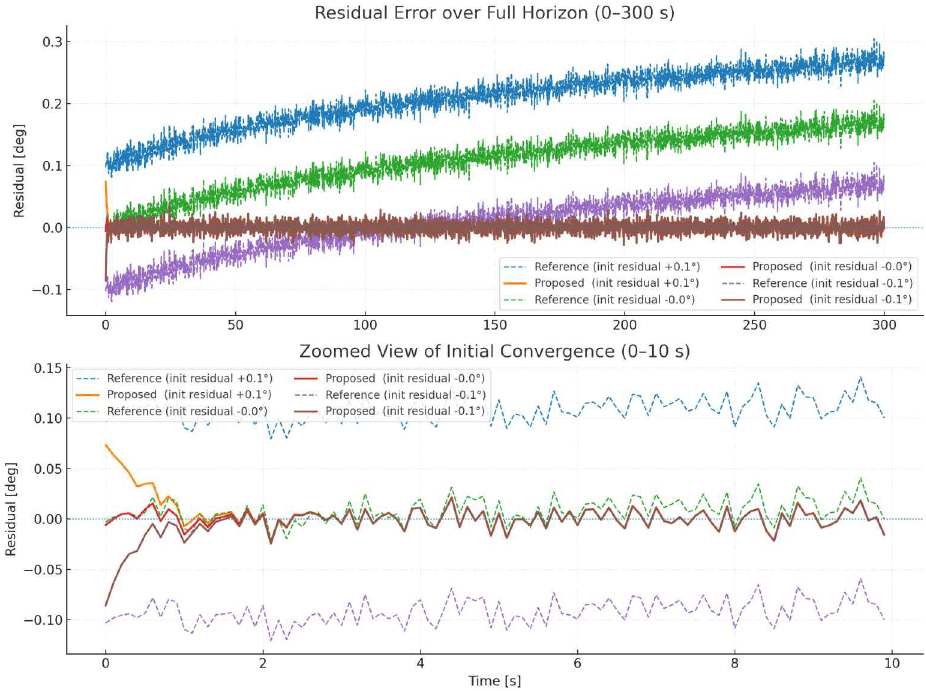
제안 기법의 강건성을 검증하기 위해, 4-5절에서 도출된 최적의 보정 반영 비율(α=.215443)을 고정한 상태에서 초기 보정값 C0을 −0.1, 0.0, +0.1°로 변화시켜 시뮬레이션을 수행하였다.
그 결과, 초기 오차 크기와 부호에 관계없이 제안 기법(proposed method)은 빠르게 0 부근으로 수렴하여 안정적인 성능을 유지하는 반면, 초기 보정만 수행한 경우(reference)는 드리프트에 따라 잔차 오차가 누적됨을 확인할 수 있었다(그림 5).
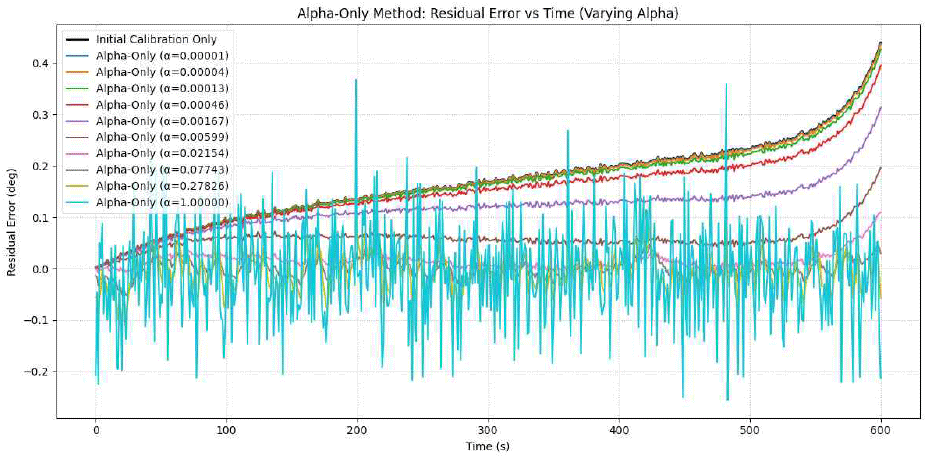
본 시뮬레이션에서는 α 값을 변화시켜가며 각 보정 방법의 잔차 오차(residual error) 변화 양상을 분석하고 최적의 α 값을 탐색하였다.
Alpha-Only 방법은 α 값 변화에 따라 잔차 오차의 안정성이 달라지는 것을 보여준다. 그림 6은 alpha-only 방법에서 다양한 α 값에 따른 잔차 오차 곡선을 나타낸다. α 값이 너무 작으면 드리프트 추적이 느려 오차가 누적되고, 너무 크면 측정 노이즈에 민감하게 반응하여 오차 변동성이 커지는 경향을 보인다. 시뮬레이션 결과, 최적의 α 값은 약 0.07743으로 나타났다.
이를 통해 제안 기법이 초기 보정값의 설정에 강건함을 보임을 알 수 있으며, 따라서 이후의 모든 실험은 C0=0.0°로 고정하여 진행한다.
제안 기법은 Alpha-Only 방법에 비해 전반적으로 잔차 오차의 변동성이 작고 안정적인 추적 성능을 보인다. 그림 7은 제안 기법에서 다양한 α 값에 따른 잔차 오차 곡선을 나타낸다. 특히 α 값이 큰 경우에도 오차가 비교적 잘 억제되는 특성을 확인하였다. 제안 기법의 최적 α값은 약 0.129155로 나타났다.
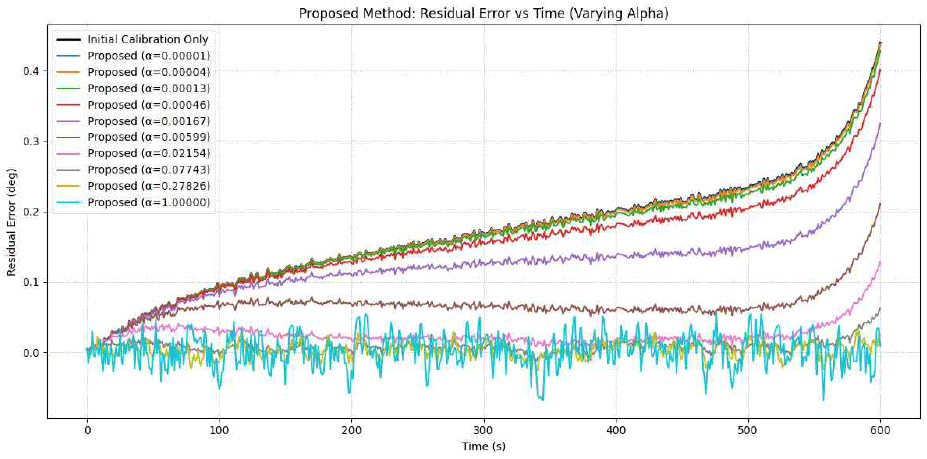
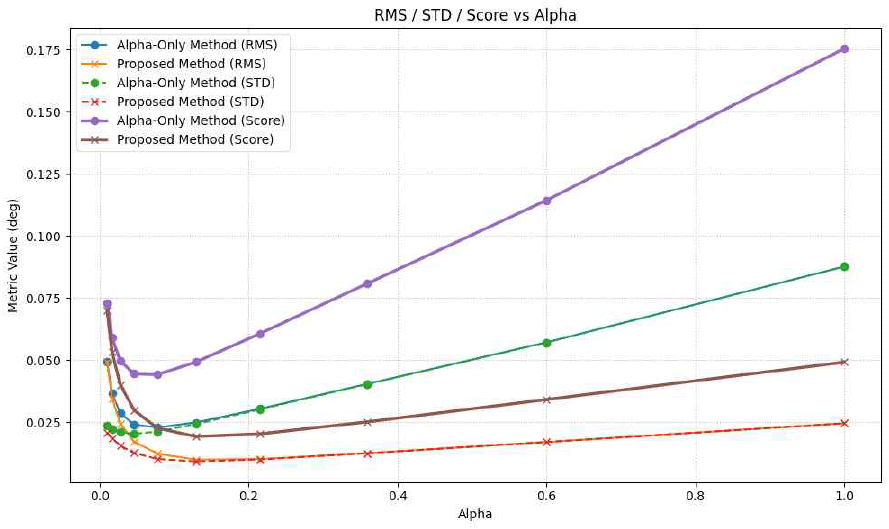
그림 8은 initial calibration only[9],[10], alpha-only method[8],[12], proposed method 세 가지 경우에 대해 α 변화에 따른 RMS(root mean square), STD(standard deviation), 그리고 Score (RMS+STD) 지표를 비교한 결과이다. 제안 기법이 alpha-only method에 비해 모든 α값에서 낮은 RMS와 STD를 나타내어 드리프트 보정 성능이 더 우수함을 입증하였다. 특히 score 지표에서도 제안 기법의 우월성이 확인되었다.
제안 기법에서 Nburst (버스트 샘플 수) 변화가 성능에 미치는 영향을 분석하였다. α=0.2 또는 최적 α(= 0.215443)를 적용하고 Nburst를 50, 100, 200으로 변화시키며 시뮬레이션을 수행하였다.
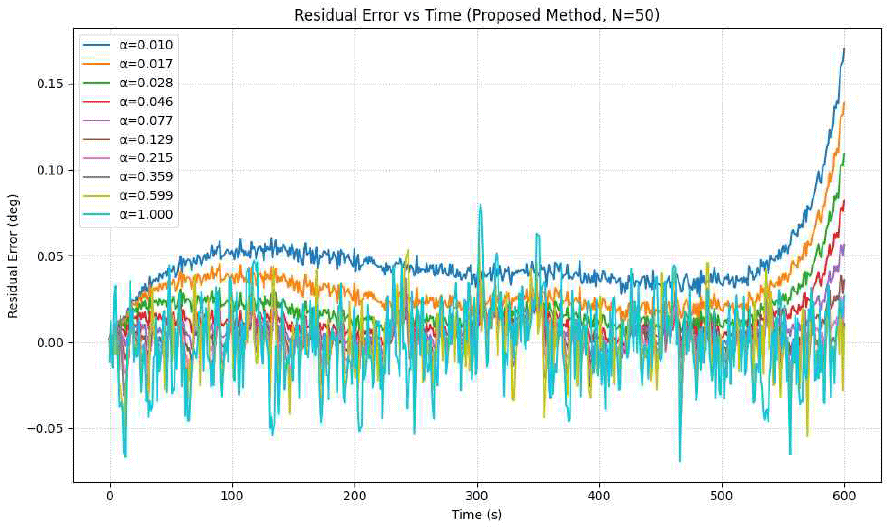
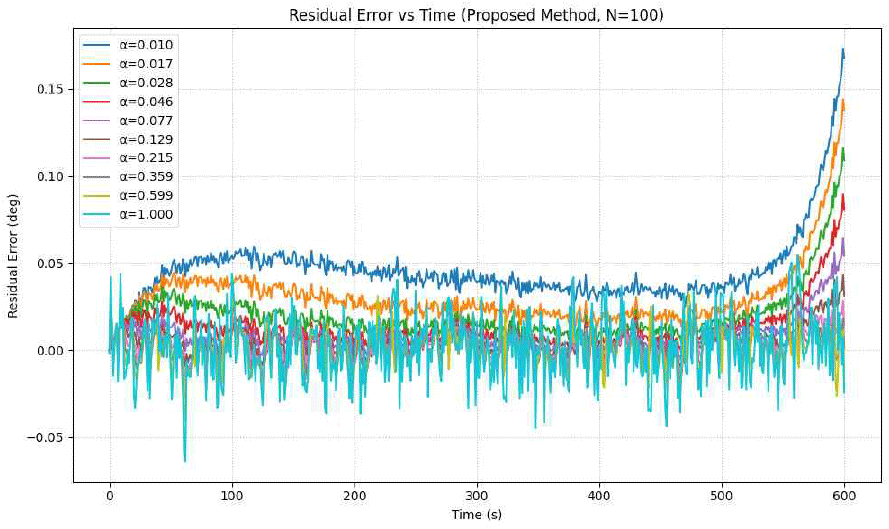
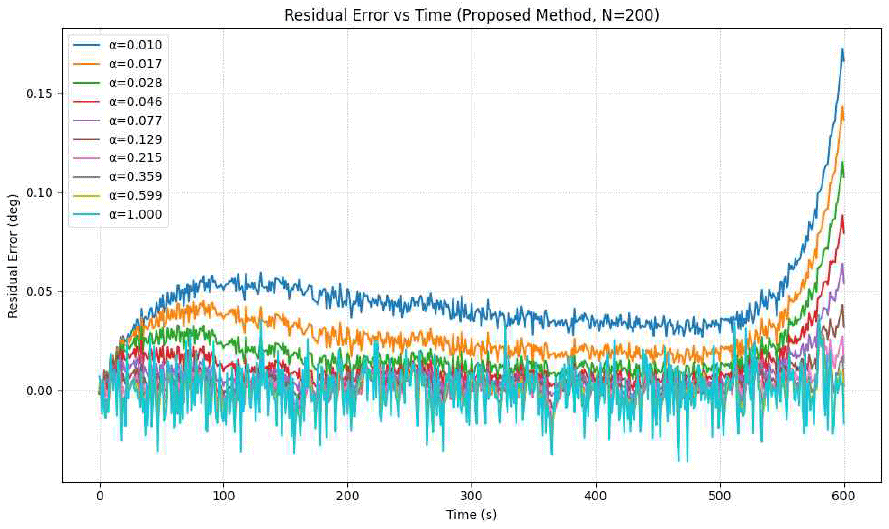
그림 9~그림 11은 각각 Nburst=50, 100, 200일 때 α 값 변화에 따른 잔차 오차 곡선을 보여준다. Nburst가 증가할수록 잔차 오차의 변동성이 감소하고 안정성이 향상되는 경향을 보였다. 이는 더 많은 샘플이 통계적 추정의 신뢰도를 높여 보정 정확도를 향상시키기 때문이다.
또한, 그림 12는 α=0.2로 고정하고 Nburst를 변화시켰을 때의 잔차 오차를 비교한 그래프로, Nburst 증가에 따른 안정성 향상을 다시 한번 보여준다.
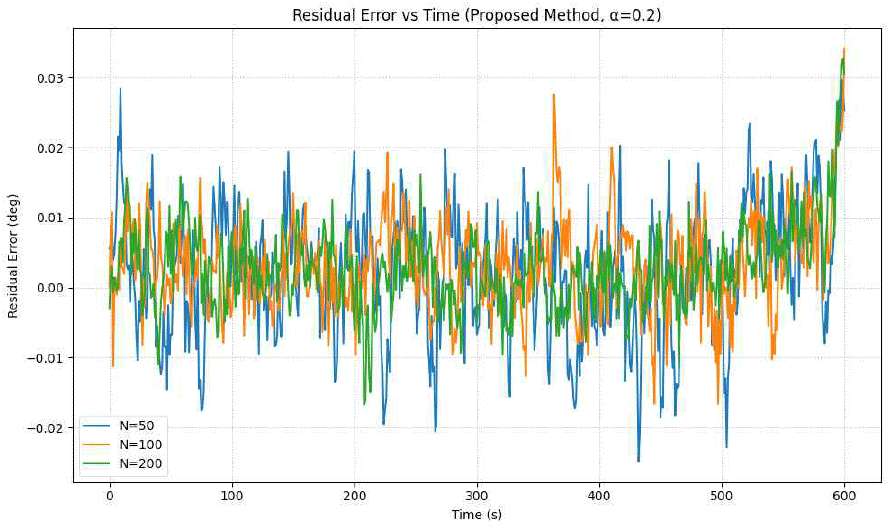
표 2는 다양한 α값과 Nburst=50,100,200에 따른 RMS, STD, Score 값을 정리한 것이다. 전반적으로 Nburst 값이 증가할수록 동일한 α에서 RMS와 STD 값이 감소하는 경향을 보였다. 특히 α=0.129155에서 N=200일 때 RMS=0.008370, STD=0.006531, Score=0.014901로 가장 낮은 값 중 하나를 기록하였다. 이는 실시간성(적은 샘플 수)과 추정 신뢰도 사이의 트레이드오프 관계를 보여주며, 적절한 Nburst 선택이 중요함을 시사한다.
앞선 절(4-6 이하)에서는 보정 주기를 100 ms로 고정하여 성능을 분석하였다. 본 절에서는 보정 주기를 1초 이상으로 확장하여 성능 변화를 검토한다. 즉, Nburst=100, α=0.215443으로 고정한 상태에서 보정 주기(Tupdate)를 1, 10, 30, 60초로 변화시키며 시뮬레이션을 수행하였으며, 이를 통해 제안 기법의 보정 주기 변화에 대한 성능 영향 및 견고성을 평가하였다.
그림 13은 다양한 보정 주기에 따른 잔차 오차 곡선을 보여준다. 보정 주기가 길어질수록 드리프트에 대한 실시간 추적 응답성이 저하되어 잔차 오차가 점진적으로 누적되고 증가하는 경향을 보였다. 보정 주기가 짧을수록 드리프트 변화를 효과적으로 추적하여 오차를 낮게 유지하는 것을 확인하였다.
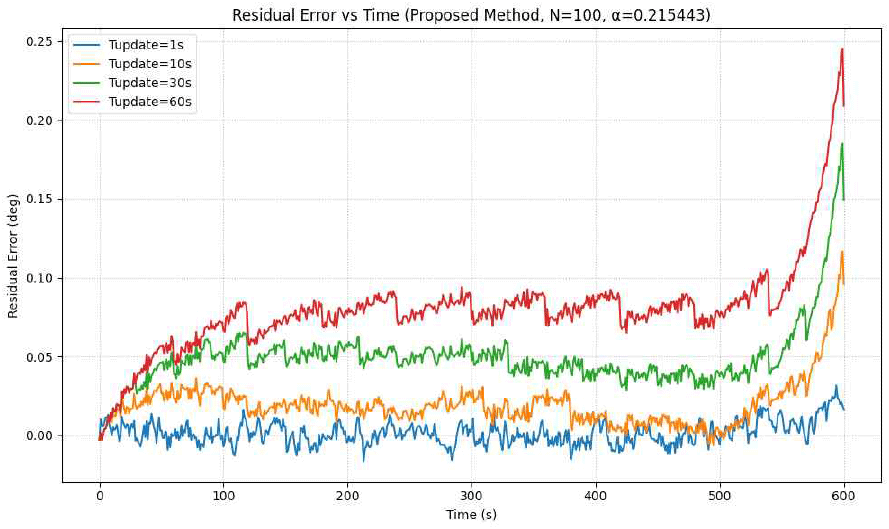
표 3은 Tupdate 변화에 따른 RMS, STD, Score 지표를 정리한 것이다. Tupdate가 1초, 10초, 30초, 60초로 증가함에 따라 모든 지표가 급격히 악화되는 것을 확인하였다. 이는 보정 주기가 드리프트 억제 성능에 매우 중요한 영향을 미침을 시사한다.
| Tupdate(s) | RMS | STD | Score |
|---|---|---|---|
| 1 | 1 | 0.007988 | 0.006793 |
| 10 | 10 | 0.029582 | 0.016203 |
| 30 | 30 | 0.06042 | 0.022028 |
| 60 | 60 | 0.092473 | 0.031399 |
앞선 4-5절에서 도출된 최적 α를 유지한 상태에서, 1 alpha-only method, proposed method를 비교하였다. 이를 통해 제안 기법의 우수성을 시각적·정량적으로 입증하였다.
그림 14는 각 방법의 최적 α를 사용하여 1초 보정 주기에서 잔차 오차를 비교한 결과이다. initial calibration only는 시간이 지남에 따라 드리프트가 누적되어 잔차 오차가 급격히 증가하는 반면, alpha-only method와 proposed method는 드리프트 추적 및 오차 억제 성능이 훨씬 우수하였다. 특히 proposed method는 alpha-only method보다 더 낮은 잔차 오차 수준과 안정적인 추적 성능을 일관되게 보여주었다.
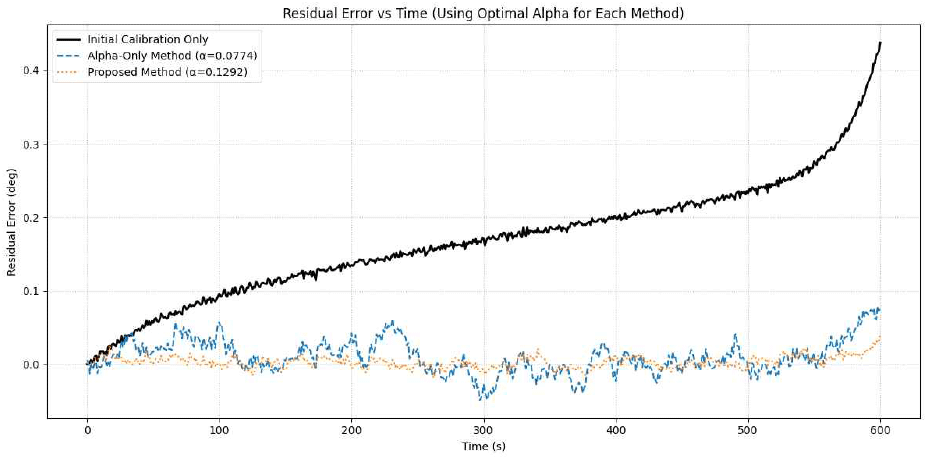
표 4는 1초 보정 주기에서 세 가지 방법의 RMS, STD, Score 지표를 수치적으로 비교한 것이다. 제안 기법은 압도적으로 낮은 오차를 보이며, 장기간 운용 시 발생하는 드리프트를 효과적으로 보정하였다. 결론적으로, 제안 기법은 1초 보정 주기 적용 시에도 드리프트 추적 성능을 유지하면서 탐지거리 및 SNR 손실을 최소화하였다. 이는 시스템 운용 부담을 줄이면서도 고정밀 보정을 달성할 수 있음을 보여주며, 제안 기법의 실용적 가치와 우수성을 입증한다.
| Method | RMS | STD | Score |
|---|---|---|---|
| Initial calibration only | 0.187021 | 0.079774 | 0.266795 |
| Alpha-only method | 0.022124 | 0.021926 | 0.04405 |
| Proposed method | 0.007995 | 0.007654 | 0.015649 |
※ Results obtained with Tupdate = 1 s.
Ⅴ. 결 론
본 논문은 모노펄스 레이더의 장기간 고정밀 각도 측정 성능 유지를 위한 통계 기반의 실시간 버스트 보정 기법을 제안하였다. 제안된 방법은 드리프트 추정의 강인성을 높이기 위해 측정 오차 샘플에서 이상치를 제거하는 절사 평균(trimmed mean)과, 샘플 신뢰도에 기반한 적응적 가중치(adaptive weighting), 그리고 과도한 보정을 억제하여 시스템 안정성을 확보하는 이중 클리핑 및 갱신 문턱값(update thresholding) 기법을 통합하였다.
다양한 시뮬레이션 결과는 제안 기법의 우수성을 입증한다. 보정 반영 비율 α 변화에 따른 분석에서, 제안 기법은 alpha-only 방식에 비해 전반적으로 낮은 잔차 오차와 높은 안정성을 보였으며, RMS, STD, score 지표에서 뛰어난 성능을 나타냈다. 또한, 샘플 수(Nburst) 변화를 통해 적절한 샘플 수가 보정 정확도와 안정성 향상에 기여함을 확인하였다. 보정 주기(Tupdate)가 짧을수록 드리프트 추적 성능이 우수하며, 이는 실시간 보정의 중요성을 강조한다. 최종적으로, 초기 보정만 수행한 경우와 alpha-only 방법과의 비교를 통해 제안 기법이 드리프트를 효과적으로 보상하여 시스템의 장기간 고정밀 운용을 가능하게 함을 정량적으로 입증하였다.
본 연구는 외부 참조원 없이 레이더 자체 신호만을 활용하여 드리프트를 실시간으로 추적·보정할 수 있는 기법을 제안하고, 시뮬레이션을 통해 그 성능을 검증하였다. 다만 본 연구에서 사용된 파라미터 값들은 시뮬레이션 기반으로 최적화된 것이며, 실제 레이더 시스템 환경에서의 추가 검증이 필요하다. 향후 연구에서는 실제 모노펄스 레이더 하드웨어 환경에서 필드 시험을 수행하여 제안 기법의 유효성을 실험적으로 입증하고, 다양한 운용 시나리오에서 파라미터 설정의 타당성을 보완할 예정이다.





