The Journal of Korean Institute of Electromagnetic Engineering and Science

The Korean Institute of Electromagnetic Engineering and Science

J. Korean Inst. Electromagn. Eng. Sci. 2025; 36(11):1073-1080

pISSN: 1226-3133, eISSN: 2288-226X

DOI: https://doi.org/10.5515/KJKIEES.2025.36.11.1073

논문/REGULAR PAPERS

긴 톱니파 Chirp FMCW 레이다의 속도 모호성 완화 기법

문관우

, 이시준^*

, 최현환^*

, 서은진

, 최서령

, 태용

, 송림^**

, 김병성^**^,^†

Techniques for Velocity Ambiguity Mitigation in Long Sawtooth Chirp FMCW Radars

Kwan-Woo Moon

, Si-Jun Lee^*

, Hyun-Hwan Choi^*

, Eun-Jin Seo

, Seo-Rueong Choi

, Yong Tae

, Reem Song^**

, Byung-Sung Kim^**^,^†

성균관대학교 전자전기컴퓨터공학과

^*성균관대학교 반도체융합공학과

^**성균관대학교 정보통신대학

Department of Electrical and Computer Engineering, Sungkyunkwan University

^*Department of Semiconductor Convergence Engineering, Sungkyunkwan University

^**College of Information and Communication Engineering, Sungkyunkwan University

^†Corresponding Author: Byung-Sung Kim (e-mail: bskimice@skku.edu)

© Copyright 2025 The Korean Institute of Electromagnetic Engineering and Science. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Sep 05, 2025; Revised: Oct 09, 2025; Accepted: Oct 28, 2025

Published Online: Nov 30, 2025

요 약

톱니파 FMCW 레이다에서 이동체의 속도를 정확히 측정하기 위해서는 속도에 반비례하는 매우 짧은 선형 chirp 파형이 요구된다. 그러나 PLL의 대역폭 및 선형성 한계로 인해 고속·광대역 chirp 파형을 구현하는 데에는 제약이 존재한다. 본 논문은 긴 chirp에서 발생하는 도플러 aliasing으로 인한 속도 모호성을, ACC(accurate frequency estimator) 기반 서브-빈 거리 보정과 거리-시간 궤적의 LS(least squares) 기울기, 그리고 도플러 FFT 융합으로 해소하는 단일 프레임 속도 추정 기법을 제안한다. 제안한 알고리즘은 시뮬레이션과 W-대역 레이다 시스템 실측을 통해 검증되었으며, chirp 지속 시간에 의해 제한되는 최대 속도를 초과하는 물체에 대해서도 정확한 속도 추정이 가능함을 확인하였다.

Abstract

An accurate velocity measurement in a sawtooth FMCW radar requires extremely short linear chirp signals that are inversely proportional to the target velocity. However, the limited bandwidth and linearity of phase-locked loops (PLLs) impose constraints on the generation of high-speed and wideband chirps. This paper proposed a single-frame velocity estimation method that resolves the velocity ambiguity caused by Doppler aliasing in long chirps by fusing accurate frequency estimator (ACC) based sub-bin range refinement, the least-squares slope of the range-time trajectory, and a Doppler FFT. Both simulations and measurements using a W-band radar system verified that the method enabled the accurate estimation of target velocities exceeding the maximum velocity limit imposed by the chirp duration.

Keywords: FMCW Radar; W-Band; Velocity Ambiguity; Least Square Method; ACC Algorithm

I. 서 론

최근 레이다 시스템은 비행체 탐지, 자율주행, 의료용 연구 및 모니터링 등 다양한 분야에서 활용되고 있다^[1],[2]. 특히 자율주행 시 주변 환경을 인식하기 위한 센서로서 주위 조도 및 악천후 환경에서 카메라 센서에 비해 강점을 지니고 있으며 라이다보다 가격이 저렴하여 차세대 센서로 주목받고 있다^[3]. 또한 MIMO(multiple-input multiple-output) 구조를 활용하여 높은 해상도를 이용한 이미징 레이다 기술이 주목받고 있다. 레이다의 톱니파 chirp 신호 발생에 핵심적으로 사용되는 PLL은 넓은 대역폭을 확보하고 주파수의 선형성을 향상시키기 위해 일반적으로 긴 chirp 시간을 필요로 한다. 긴 chirp 시간은 주파수 변화율을 완화하여 안정적으로 동작할 수 있도록 하지만, 속도 추정에 있어 속도 모호성이 증가하는 문제가 발생한다.

기존의 속도 모호성을 해결하는 방법 중 하나는 다중 프레임 신호를 이용하는 방식이다. 예를 들어 서로 다른 중심 주파수를 이용하여 속도 모호성을 해결하거나 서로 다른 PRF(pulse repetition frequencies)를 이용하여 서로 다른 속도 모호성을 가진 두 신호를 CRT(chinese remainder theorem)를 이용하여 해결한다^[4],[5]. 그러나 이러한 방법들은 다중 프레임을 이용하여 높은 메모리양을 요구하며 높은 시스템 복잡성으로 인해 실시간 처리 시 표적 탐지 지연이 발생한다^[6].

본 논문에서는 속도 모호성의 해결 및 낮은 연산 복잡도에 목적을 두고 ACC(accurate frequency estimator) 알고리즘을 이용하여 고정밀 거리 측정을 한 뒤 최소제곱법을 이용한 거리변화량 기반 속도 추정을 이용하여 도플러 FFT 기반 속도 추정의 속도 모호성을 해결한다^[6],[7]. 제안한 기법은 단일 프레임 내에서 추정이 가능하며 연산의 복잡도 또한 낮기에 실시간 처리에 강점이 있다. Ⅱ절에서는 FMCW 레이다의 속도 추정 신호 모델을 기술하며 Ⅲ절은 ACC 기법과 최소제곱법에 대해 간단히 설명한 후 제안한 알고리즘을 설명한다. Ⅳ절은 측정 시에 사용한 FMCW 레이다를 소개한 후 Ⅴ절에서는 시뮬레이션 및 해당 레이다로 측정한 결과를 제시한다.

Ⅱ. FMCW 레이다 신호 모델

움직이는 표적에 대한 비트 신호는 식 (1)과 같이 표현할 수 있다.

s t = A' exp j 2 π f i f + f d t + ϕ

(1)

f_if는 비트 주파수, f_d는 도플러 주파수를 의미하며 ϕ는 초기 위상을 의미한다. 이 신호에서 거리에 해당하는 주파수의 경우 아래의 식 (2)와 같다.

f i f = B T c × τ = 2 S R c

(2)

B는 대역폭, T_c는 chirp 시간을 의미하며 S는 chirp의 기울기로 B/T_c이다. 이를 adc 샘플링 주파수 f_s에 의해 N개의 포인트로 이산화된 신호를 FFT하여 거리를 구하게 될 경우 아래의 식 (3) 및 식 (4)와 같이 정리할 수 있다.

R^= c 2 S k r f s N k r = 0, 1, ⋯ N − 1

(3)

Δ R = c 2 B

(4)

f_d를 표현하면 아래의 식 (5)와 같다.

f d = 2 v f c c = 2 v λ

(5)

비트 신호에서 chirp 개수 M개의 방향으로 FFT를 하게 될 경우 도플러 주파수를 얻게 되며 이때 해당하는 속도는 아래의 식(6) 및 식 (7)과 같다.

v^= λ 2 k d − M / 2 M T c k d = 0, 1, ⋯, M − 1

(6)

− λ 4 T c ≤ v < λ 4 T c

(7)

도플러 주파수를 이용하여 속도를 추정할 경우 위 식(7)과 같이 추정 가능한 속도 범위가 제한된다. 중심 주파수 대역이 높을수록, chirp 시간이 길수록 추정 가능한 속도의 범위는 줄어든다.

Ⅲ. 속도 추정 기법

FFT의 주파수 해상도는 $f s N$ 로 결정되기에 실제 주파수 f_if가 해당 FFT 빈에 정확하게 일치하지 않을 경우 해당 스펙트럼은 인접한 구간으로 에너지가 분산된다. 창함수를 적용하지 않는 사각창 FFT에서는 주파수 불일치로 인한 straddle loss가 발생하며 이는 일반 FFT보다 제로 패딩 FFT에서 다소 완화된다. ACC 알고리즘은 이 성질을 이용하여 잔차 위상을 보정하는 후처리 알고리즘이다. 해당 알고리즘의 경우 손실된 인접 빈에서의 위상차를 이용하여 보정값을 직접 추정하여 제로 패딩에 비해 연산량이 현저히 적다. ACC는 다음 3단계로 구성된다^[7].

1. FFT한 결과값에서 표적에 해당하는 k_r을 찾고 인접한 FFT 빈에 대해서 위상차를 이용하여 주파수 편차 방향을 인식한다. 기준 위상은 $Φ r e f = N + 1 π N π$ 라고 했을 때, 아래와 같이 정리할 수 있다. ϕ_p는 기준 빈과 다음 빈과의 위상차이며 ϕ_n는 기준 빈과 이전 빈과의 위상차이다.

ϕ p = mod ∠ X k r + 1 − ∠ X k r, 2 π ϕ n = mod ∠ X k r − 1 − ∠ X k r, 2 π

(8)

k e f f = k r + 1, ϕ p − Φ r e f ≤ ϕ n − Φ r e f k r − 1, ϕ p − Φ r e f > ϕ n − Φ r e f

(9)

2. 치우쳐 있는 방향의 빈과 위상 차이를 이용하여 빈 해상도 이하의 세부적인 주파수 보정값은 $δ^A C C$ 을 구한 뒤 주파수 보정을 수행한다.

δ^A C C = N π × a r c o t X k r X k r + 1 + cos π N sin π N, δ ≥ 0 − N π × a r c o t X k r X k r − 1 + cos π N sin π N, δ < 0

(10)

3. 추정된 피크 빈과 세부 보정값을 합산하여 최종 주파수 $f^if$ 를 계산한다.

f^if = k r + δ^A C C × f s N

(11)

각 chirp마다 ACC 알고리즘 기반으로 거리를 정밀하게 추정하여 표적의 절대 거리를 산출한다. 해당 알고리즘을 이용하여 구한 정밀한 거리의 변화는 최소제곱법을 이용하여 1차로 근사한 기울기 a*를 이용하여 속도 v*를 구한다.

a * = arg min a 12 ∑ m = 1 M r m − a × m + b 2

(12)

v * = a * Δ R T c

(13)

최소제곱법으로 구한 속도는 모호성은 없지만 chirp별 추정이기에 잡음에 상대적으로 취약하다. 반면, 도플러 FFT 기반의 속도 추정 $v^F F T$ 의 경우 모든 chirp의 위상 정보를 누적하므로 잡음에 강하지만 속도의 모호성이 존재한다. 따라서 최소제곱법으로 구한 속도를 도플러 FFT의 모호구간 선택 기준으로 활용한다. 도플러 모호성 간격은 2V_max로 주어지며 가능한 속도 후보의 집합 C는 아래의 식 (14)와 같이 정리된다.

C = v^F F T + 2 V max ⋅ k, k ∈ − K, K

(14)

이 때, K는 실용적 탐색 범위이며 단일 프레임 내 최소제곱법으로 구한 속도와의 차이가 최소가 되는 k를 적용한다.

k * = arg k ∈ − K, K min C − v *

(15)

거리 변화 기반 속도 추정은 넓은 비모호 범위에서 올바른 모호성 구간을 지시하며 도플러 FFT 기반의 추정 속도는 그 구간 내 정밀한 위치를 제공한다. 도플러 FFT에 ACC 알고리즘을 한 번 더 사용하여 구간 내의 속도를 보다 정밀한 위치를 제공하여 실제 속도 추정의 정확도를 높인다(그림 1).

그림 1. | Fig. 1. 단일 프레임 속도 모호성 해소 기법 순서도 | Flow chart of unambiguity velocity estimation in a single frame method.

Download Original Figure

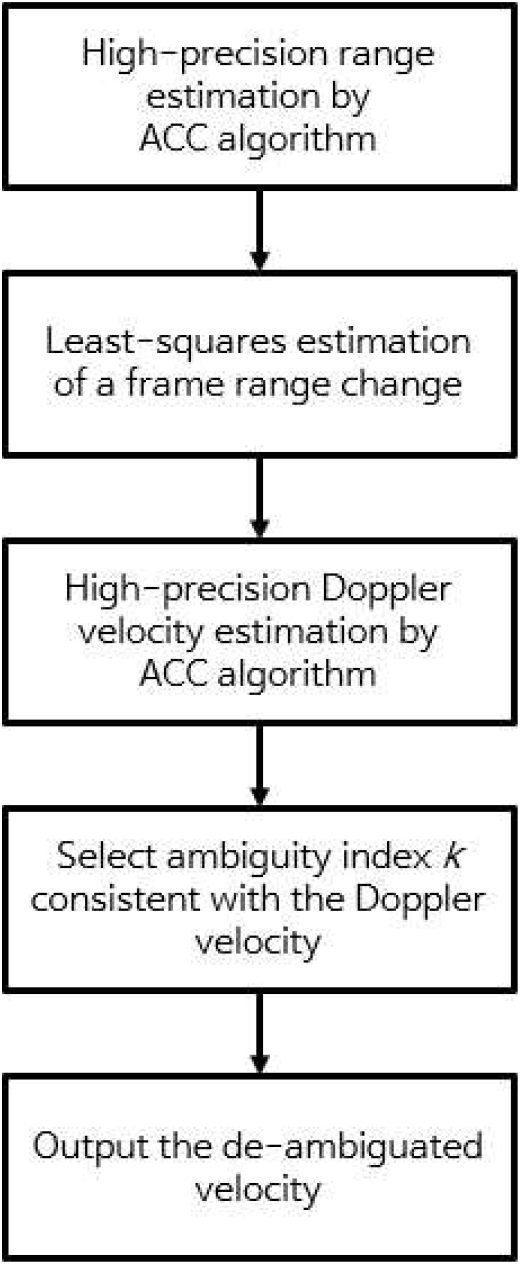
따라서 최종 추정 속도 $v^$ 는 아래 식 (16)과 같이 정리된다.

v^= v F F T A C C * + 2 v max × k *

(16)

Ⅳ. W-대역 FMCW 레이다 시스템

본 논문에서 소개하는 알고리즘의 검증을 위해 사용한 W-대역 레이다 시스템은 8개의 1채널의 송신기와 4개의 4채널의 수신기로 구성되어 있다(그림 2).

그림 2. | Fig. 2. W-대역 FMCW 레이다 정면 및 측면 사진 | The front and side view of the W-band radar module.

Download Original Figure

송신기 및 수신기는 28 nm CMOS공정으로 제작되었으며 칩과 안테나는 직접 급전하였다. 데이터 수집은 8채널 ADC 보드를 이용하여 FPGA로 데이터를 수집하였다. 안테나는 송신기 중앙급전 3-패치 배열을 이용하여 시뮬레이션 이득을 10.9 dBi, 수신기 9.6 dBi를 확보하였다^[8].

중심 주파수는 93 GHz이며 대역폭은 2 GHz, chirp 시간은 400 μs의 톱니파를 이용하였다. 이때 데이터 처리를 위하여 톱니파 chirp이 끝나면 데이터 처리를 위하여 대기 시간 200 μs를 가지며 한 프레임에 총 60개의 chirp을 이용하였다. 이로 인해 도플러 FFT로 속도를 구하게 되면 식 (7)에 의해 ±1.330 m/s의 속도 범위 내에서만 속도 모호성이 발생하지 않는다.

Ⅴ. 시뮬레이션 및 측정 결과 분석

본 논문에서 제안하는 알고리즘의 연산량은 기존의 FFT한 데이터를 재사용하기에 기본적인 2차원 FFT의 연산 복잡도는 O(NM log(NM))가 된다. N은 거리 FFT의 길이이며 M은 도플러 FFT의 길이이다. 추가로 국소 구간 W만큼의 피크 탐색 O(W), 위상의 방향을 판별하는 연산량 O(1)를 chirp의 개수 T만큼 반복하여 O(TW)가 된다. 최소제곱법의 연산량 O(T), 도플러 FFT의 열 M개에서 최댓값 탐색은 O(M), 모호성 해소는 O(1)로 최종적으로 추가적인 연산 복잡도는 다음과 같이 근사할 수 있다.

O T W + O T + O M ≈ O T W + O M

(17)

해당 알고리즘의 정확도를 평가하기 위해 알고리즘의 몬테카를로 방법을 이용하여 시뮬레이션을 진행하였다. 해당 알고리즘은 거리에 대한 정보를 사용하기에 거리 FFT에 대한 RMSE(root mean square error)를 중심적으로 확인하였다.

그림 3은 거리 FFT에서의 각각의 알고리즘의 RMSE를 비교한 그래프이다. 해당 데이터는 제안하는 알고리즘과 유사한 알고리즘의 RMSE이다. SNR이 −13 dB 이후부터는 두 알고리즘 모두 CRB(cramar-rao bound)에 근접함을 확인할 수 있다. 다음은 각 단계별로 걸리는 연산 시간을 표로 도출하였다. 해당 연산 시간은 intel 사의 i7-9700K CPU @ 3.6 GHz가 탑재된 데스크탑을 이용하여 측정하였다.

그림 3. | Fig. 3. 거리 FFT의 RMSE와 CRB의 비교 | The comparison of RMSE of Range FFT.

Download Original Figure

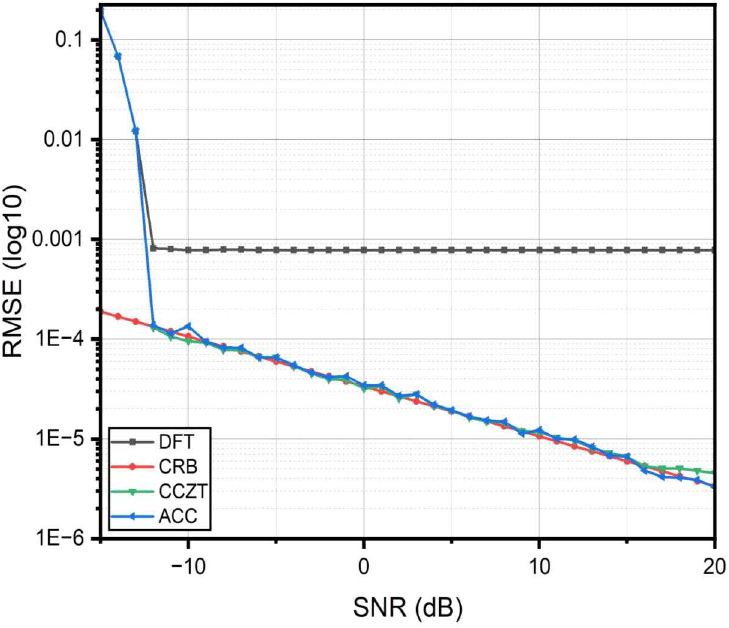
본 연구는 단일 프레임 내에서 속도 모호성을 해소하는 방법의 정확도와 실시간성을 평가하는 것을 목표로 하였다. 이에 따라 CCZT(coherent chirp-Z transform) 기반 알고리즘^[6]을 비교 기준으로 채택하였다. CCZT 알고리즘은 고정밀 주파수 보간에 기반한 대표적인 알고리즘으로, ACC 알고리즘과 유사하게 고정밀 주파수 보간이라는 목적에서 비교가 가능한 기준으로 선정하였다.

그림 3과 표 1에서 확인할 수 있듯이, 정확도 측면에서는 CCZT와 유사하게 CRB에 근접하지만, 연산 복잡도와 실행 시간에서 제안 기법이 우수함을 확인하였다.

표 1. | Table 1. 실행 시간표 | Execution time table.

	Precise range estimation	LS-based velocity	Doppler FFT-based velocity	Total time
Proposed algorithm	2.462 ms	0.011 ms	0.006 ms	2.479 ms
CCZT-based algorithm	12.42 ms	0.011 ms	0.004 ms	12.435 ms

Download Excel Table

본 연구에서는 거리 FFT 결과를 기준으로 한 프레임 내에서 표적의 거리 변화가 존재할 경우 고속 이동으로, 변화가 없을 경우 저속 이동으로 정의하였다.

그림 4는 이동하는 표적의 속도를 측정한 환경이며 표적은 코너 리플렉터를 이용하였다. 제안한 기법의 속도 추정 정확도를 검증하기 위하여 chirp 시간 160 μs을 사용하는 상대적으로 빠른 고속첩을 이용한 77 GHz TI AWR1843 BOOST 모듈을 사용하여 동일한 환경에서 실험을 진행하였다. 속도 범위 ±6.09 m/s 조건에서 짧은 chirp을 이용한 본 기법과 매우 유사한 약 3.21 m/s 및 −1.15 m/s의 속도가 관측되었음을 확인하였다.

그림 4. | Fig. 4. 이동 표적 측정 환경 | The environment of moving target measurement.

Download Original Figure

그림 5는 1차원 FFT에서 구한 표적의 거리 및 ACC 알고리즘 적용, 최소제곱법을 적용한 데이터를 각 chirp에 대하여 표시한 그래프이다. 거리의 변화량을 기반으로 구한 속도는 3.1823 m/s이며 2차원 FFT 및 ACC 알고리즘을 이용하여 구한 속도는 0.5726 m/s이다. 최종적으로 추정한 표적의 속도는 3.2322 m/s로 도출된다.

그림 5. | Fig. 5. 고속 이동 표적 측정 결과 | The Result of fast moving target measurement.

Download Original Figure

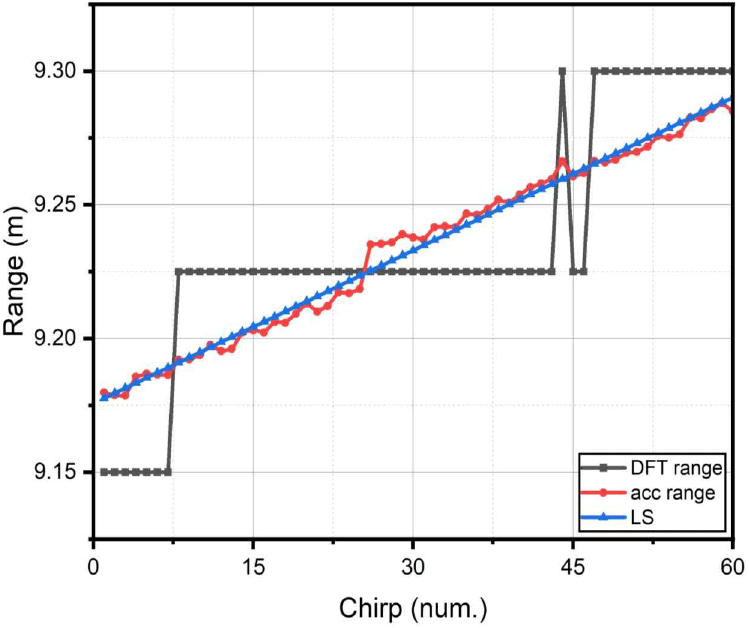
그림 6은 저속 이동 표적의 측정 결과이며 1차원 FFT에서 거리의 변화가 없는 것을 확인할 수 있다. 그러나 ACC 알고리즘을 이용하면 거리의 변화가 발생하며 최소제곱법을 이용하여 거리 변화의 추이에 대한 정보를 얻을 수 있다. 본 논문의 기법으로 구한 속도는 −1.4975 m/s로 나왔으며 도플러 FFT 및 ACC 알고리즘으로 구한 속도는 −1.0751 m/s로 나와 최종적으로 −1.0751 m/s로 속도로 표적이 이동한다는 것을 확인하였다.

그림 6. | Fig. 6. 저속 이동 표적 측정 결과 | The result of slow moving target measurement.

Download Original Figure

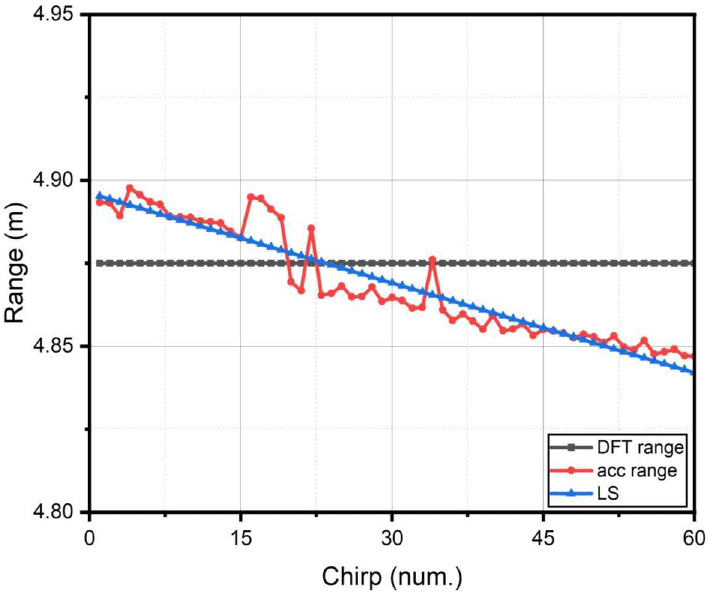
FFT 기반 속도는 이산 주파수 축에서 계산되므로, 실제 속도 변화가 연속적이더라도 일정 빈에 머물다 인접 빈으로 급격히 이동하는 형태로 나타난다. 반면 ACC 알고리즘은 인접 빈 간 위상차를 이용해 주파수 오프셋을 보정하므로, FFT보다 연속적이고 부드러운 속도 변화를 보이며 LS(최소제곱법) 속도는 ACC로 구한 거리-시간 데이터를 1차로 근사한 결과이다. 저속 표적의 경우 거리 변화가 작아 잡음에 의한 기울기 오차가 크게 나타날 수 있다. 본 논문에서 제안한 최종 속도는 도플러 FFT에 ACC 보정을 적용한 결과이며, 모호구간 결정은 LS 결과를 기준으로 수행된다.

Ⅵ. 결 론

본 논문은 표적의 ACC 알고리즘 기반 정밀 거리 분석을 토대로 최소제곱법(LS)을 적용하여 표적의 대략적인 속도를 산출하고, 이를 도플러 FFT 및 ACC 알고리즘으로 얻은 모호한 속도와 비교하여 정확한 속도를 추정하는 새로운 기법을 제안하였다. 제시된 방법은 연산 부하가 적고 단일 프레임만으로도 속도 추정이 가능하다는 장점을 지니므로, 실시간 응용에 적합하다. 특히 비교적 긴 chirp 시간을 요구하는 레이다 시스템에서 속도 추정의 정확도를 향상시키는 데 기여할 수 있으며, 향후 자동차 레이다, 모션 인식 레이다 등 다양한 응용 분야에서 활용 가능성이 높을 것으로 기대된다.

References

[1].

X. Li, X. Wang, Q. Yang, and S. Fu, “Signal processing for TDM MIMO FMCW millimeter-wave radar sensors,” IEEE Access, vol. 9, pp. 167959-167971, Dec. 2021.

[2].

D. Jung, S. Cheon, D. Kim, J. Yoon, and B. Kim, “Short-time remote heart rate measurement based on mmWave FMCW radar frame structure,” IEEE Antennas and Wireless Propagation Letters, vol. 22, no. 6, pp. 1301-1305, Jun. 2023.

[3].

R. V. Pulayath, K. S. Sathyanarayanan, P. B. Akash, K. S. Amisha, K. M. Arun Prasad, and P. J. Shaija, “Review on mmWave radar sensor for 3-D mapping,” in 2025 2nd International Conference on Trends in Engineering Systems and Technologies(ICTEST), Ernakulam, Apr. 2025, pp. 1-8.

[4].

M. Kronauge, H. Rohling, “New chirp sequence radar waveform,” IEEE Transactions on Aerospace and Electronic Systems, vol. 50, no. 4, pp. 2870-2877, Oct. 2014.

[5].

Z. Wang, J. Yu, and Y. Yang, “Resolving range and velocity ambiguity effectively and efficiently with GPU,” in 2021 CIE International Conference on Radar(Radar), Haikou, Dec. 2021, pp. 1122-1126.

[6].

Z. Xu, Y. Chen, S. Wei, and P. Zhang, “A single-frame velocity disambiguation algorithm for FMCW radar with high-precision ranging,” IET International Radar Conference(IRC 2023), Chongqing, Dec. 2023, pp. 1245-1250.

[7].

M. Wang, Q. Wang, Y. Wen, and K. Liang, “A fast and accurate frequency estimator for complex single-tone signal based on DFT interpolation,” IEEE Transactions on Instrumentation and Measurement, vol. 73, pp. 1-11, Dec. 2024.

[8].

D. Y. Yang, S. W. Kang, J. H. Park. J. B. Yoon, S. Y. Kim, and J. W. Lee, “A 94 GHz 8Tx-16Rx direct center-fed active array TD-MIMO FMCW radar in 28-nm CMOS,” in 2025 IEEE/MTT-S International Microwave Symposium - IMS 2025, San Francisco, CA, Jun. 2025, pp. 9-12.