I. 서 론
위성통신, 장거리 레이다 시스템 등에서 송수신되는 전자파는 대기권을 통과하는 과정에서 대기 굴절률, 전리층 전자밀도의 변화에 의한 굴절(refraction), 감쇠(attenuation) 및 지연(delay)과 같은 현상을 겪는다[1],[2]. 이러한 현상은 위성통신의 신호 품질과 안정성을 저해하고, 레이다의 표적 위치 추정에 오차를 일으킬 수 있다. 따라서 시스템의 성능을 최적화하고 운용의 신뢰성을 확보하기 위해서는 실시간 대기 환경을 정확히 파악하고, 이를 통해 전파 특성을 정확히 모델링해야 한다. 대기권을 통과하는 전자파의 전파 특성은 대기 굴절률에 의해 결정되며, 이는 다음과 같은 식 (1) 및 식 (2)으로 계산된다[3].
식 (1) 및 식 (2)에서 n은 굴절률, N은 굴절 계수(N-units), T는 절대 온도(K), P는 기압(hPa), e는 수증기압 (hPa)을 나타낸다. 이러한 기상 변수들의 연직 분포에 대한 측정값은 고층 기상 관측소의 라디오존데(radiosonde) 관측을 통해 획득할 수 있다. 그러나 이러한 관측소는 일부 지역에 제한적으로 분포하기 때문에, 전체 해석 영역에 대한 대기 굴절률 분포 파악에 한계가 있다.
이러한 한계를 극복하기 위해, 각 관측소에서 제공되는 측정값에 역거리 가중법(IDW, verse distance weighting)이나 크리깅(kriging)과 같은 공간보간법을 적용하여 미관측점에서의 값을 추정함으로써, 대기 굴절률의 3차원 분포를 모델링하는 방법이 사용된다[4],[5]. 그러나 단순히 관측 지점과의 통계적 상관관계만을 고려하여 미관측점의 값을 추정하기 때문에 예측 결과에 대한 물리적 일관성이 결여되어, 대기 굴절률 분포의 정확한 추정에 근본적인 한계가 있다.
이에 대안으로, 일부 지점의 측정값에 수치모델(NWP, merical weather prediction)의 초기 추정값인 배경장(background field)을 결합하여 최적의 전체 대기 상태를 추정하는 4차원 변분 자료동화(4D-Var, four-dimensional variational data assimilation) 기법이 활용될 수 있다[6],[7]. 4D-Var은 물리 법칙 기반의 수치모델에 측정값을 동화(assimilation)시키기 때문에, 미관측점에서 추정된 기상 변수들의 물리적 일관성을 보장한다는 특징이 있다. 그러나 대기 굴절률의 3차원 분포를 생성하기까지 2~3시간에 달하는 연산 시간이 소요되고, 슈퍼컴퓨터 급의 고성능 컴퓨팅 자원이 요구되기 때문에, 실시간 대기 환경을 반영해야 하는 장거리 전자파 전파 해석 분야에서의 활용에는 제약이 따른다. 따라서, 4D-Var의 계산 복잡도 문제와 전통적인 공간보간법의 물리적 비일관성 문제를 동시에 해결할 수 있는 새로운 접근법이 요구된다.
최근 기상학 분야에서는 이러한 계산 복잡도 문제를 딥러닝 모델을 활용하여 해결하려는 연구가 활발히 진행되고 있으며, 대표적으로 Google DeepMind의 GraphCast 모델이 있다[8]. ERA5 재분석 데이터(ERA5, ECMWF re-analysis 5th generation)를 학습하여 과거 두 시점의 전 지구 대기 상태(Xt-6h , Xt)로부터 다음 시점의 상태(Xt+6h)를 예측하도록 설계된 GraphCast는 전통적인 NWP 대비 정확도 및 연산 효율 면에서 우수한 성능을 보였으며, 딥러닝 모델이 물리 기반 모델을 대체할 수 있는 새로운 가능성을 제시하였다. 그러나 대부분의 연구들은 과거의 대기 상태로부터 미래를 예측하는 예보(forecasting) 문제에 초점을 두고 있다. 반면, 일부 지점의 측정값을 이용하여 전체 대기 상태를 재구성하는 자료동화(data assimilation) 과정을 딥러닝 모델로 대체하려는 시도는 아직 미흡한 실정이다. 딥러닝 기반의 자료동화기법은 연산 자원이 크게 요구되는 4D-Var의 반복적인 물리 기반 최적화 과정을, 희소한 측정 데이터(입력)와 전체 대기 상태(출력) 간의 복잡한 비선형 관계를 학습한 딥러닝 모델로 대체하는 데이터 기반(data-driven) 접근법으로, 앞서 제기된 4D-Var의 계산 복잡도 문제와 전통적 공간보간법의 물리적 비일관성 문제를 동시에 해결할 수 있다.
이에 본 논문에서는 희소한 측정 데이터만으로 전체 대기 굴절률을 신속하게 추정하는 3D U-Net 기반 딥러닝 모델을 제안한다[9]. 제안하는 모델은 ERA5 재분석 데이터를 통해 관측 데이터와 전체 대기 상태 사이의 복잡한 비선형적 관계를 학습한다. 학습된 모델은 전통적인 자료동화의 반복적인 최적화 과정을 단 한 번의 순방향 연산으로 대체하여, 새로운 관측 데이터 입력 시 물리적으로 일관된 전체 대기 굴절률 분포를 즉각적으로 추정할 수 있다.
본 논문은 다음과 같이 구성된다. II장에서는 모델의 학습에 사용된 데이터의 전처리 과정과 학습 데이터를 구성하는 방법에 대해 제시한다. III장에서는 본 연구에서 제안하는 딥러닝 모델의 구조와 학습 방법을 기술하고, 전통적인 보간법과의 비교를 통해 모델의 성능을 정량적으로 분석한다. 마지막으로 IV장에서는 연구 결과를 요약하고 연구의 결론을 제시한다.
II. 데이터 전처리 및 학습 데이터 구성
ERA5 재분석 데이터는 과거부터 현재까지 수집된 모든 관측 자료(위성, 항공기, 지상관측, 라디오존데 등)에 최신 수치예보모델를 4D-Var 기법으로 통합하여 과거 대기 상태를 재구성한 격자형 데이터셋으로, 생성 과정의 엄밀함과 검증된 정확도를 바탕으로 다양한 기상 및 응용 분야에서 특정 시점의 대기 상태에 대한 사실상의 정답(ground truth)으로 여겨진다[10]. 하지만 이를 생성하기 위한 데이터 동화 및 재분석 과정의 복잡성으로, 2~3개월의 시간 지연이 발생하여 실시간 활용이 제한된다.
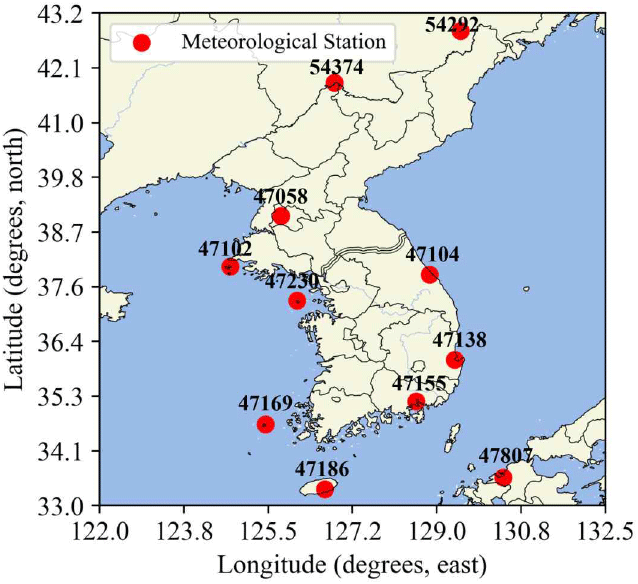
본 논문에서는 ERA5 데이터의 정확도에 준하는 대기 굴절률 분포를 즉각적으로 획득하고자, 라디오존데 관측 데이터를 입력받아 전체 대기 분포를 생성하는 딥러닝 모델을 설계하였다. 모델의 입력 데이터는 실제 위성 및 레이다 시스템 운용 환경에서 안정적으로 수집 가능한 데이터로 한정하였다. 이에 따라 한반도 및 주변국의 다수 기상 관측소 중, 12시간 간격으로 결측 없이 주기적인 데이터 제공이 보장되는 11개 지점만을 선정하였으며, 그 분포와 상세 정보는 그림 1과 표 1에 제시된 바와 같다. 최종적으로 제안하는 모델은 앞서 선정된 11개 관측소의 기상 관측 자료를 입력받아 한반도 전역의 대기 상태를 출력한다.
ERA5 재분석 데이터로부터 11개 라디오존데 관측소의 측정값과 한반도 전역의 대기 상태 간의 비선형 관계를 딥러닝 모델에 학습시키기 위해, 본 논문에서는 한반도 및 주변 해역(31.25°N~44.25°N, 122.00°E~132.50°E)에 대하여 과거 1980년 1월 1일부터 2024년 12월 31일까지의 ERA5 재분석 데이터를 1시간 간격으로 추출하여 총 394,488개의 데이터를 확보하였다[11]. ERA5의 0.25° 수평 해상도를 고려하면, 해당 영역은 53×43 크기의 격자로 정의된다.
그림 2는 ERA5 재분석 데이터로부터 딥러닝 모델의 학습 데이터를 구성하는 예시를 나타낸다. 본 논문에서 제안하는 딥러닝 모델은 라디오존데 관측 지점의 희소한(sparse) 데이터를 입력받아 전체 영역의 조밀한(dense) 대기 상태를 출력하는 구조를 갖기에, 각 시간별 ERA5 데이터는 입력 텐서(X)와 목표 텐서(Y)의 쌍으로 전처리된다.

입력 텐서와 목표 텐서는 공통적으로 각 격자점마다 37개 기압면(1,000 hPa, 975 hPa, …, 2 hPa, 1 hPa)에 대한 5개 고층 대기 변수(기온 T, 지오포텐셜 z, 상대습도 H, 동서풍 u, 남북풍 v)를 포함하는 구조를 가지며, 최종적으로 (53, 43, 37, 5) 크기의 4차원 텐서로 구성된다[12]. 목표 텐서는 53×43 전체 격자의 원본 ERA5 데이터를 그대로 사용하여 텐서를 구성하고, 입력 텐서는 전체 격자에서 11개의 라디오존데 관측 지점의 값만 남기고 나머지 영역은 0으로 마스킹(masking)함으로써 희소한 형태로 구성하였다. 5개 고층 대기 변수는 전 세계 라디오존데 관측망에서 실시간 수집이 가능한 변수들이면서 대기 역학적으로 상호 의존성을 갖는 변수들로 구성된다. 즉 5개 변수는 대기 중에서 서로 영향을 주고받으며, 한 변수의 변화가 다른 변수들의 변화를 일으키는 물리적 관계를 갖는다[13],[14]. 이러한 변수 간 물리적 상관관계는 후술할 딥러닝 모델이 희소한 관측점의 정보로부터 전체 대기 상태를 추론할 때 중요한 단서로 활용된다. 또한 이러한 변수 구성 방식은 하나의 딥러닝 모델이 대기 굴절률 계산에 필요한 기온, 기압, 습도를 단일 연산으로 동시에 출력하도록 함으로써, 전체 학습 및 추론 과정의 효율성을 높인다.
III. 3D U-Net 구조의 CNN 모델
본 논문에서는 희소한 관측 자료로부터 조밀한 대기 상태를 재구성하는 문제를 해결하기 위한 딥러닝 모델로 3D U-Net 구조의 CNN을 활용하였다. U-Net은 일반적으로 이미지 인페인팅(image inpainting) 등 일부 픽셀로부터 전체 픽셀을 재구성하는 희소-조밀 변환(sparse-to-dense reconstruction) 문제에 효과적으로 활용된다. 이미지 데이터는 인접한 픽셀 간 높은 공간적 상관관계(spatially-local correlation)를 가지며, 특정 패턴이 이미지 내 어느 위치에서든 유사하게 나타날 수 있는 위치 불변 특성(translation invariance)을 갖는다.
기상 데이터 역시 이와 유사한 특성을 갖는다. 격자점별 기상 변수들은 인접한 격자 간 강한 물리적 상관관계를 보이며, 기상 패턴은 지역에 따라 이동하면서도 그 특성을 유지한다. 따라서 위경도에 따른 다채널 기상 변수 분포는 본질적으로 다차원 이미지와 유사한 구조를 갖기에, 이미지 복원 문제에 U-Net이 효과적으로 적용된 것처럼, 희소한 관측 자료로부터 조밀한 기상 격자 정보를 재구성하는 문제에도 U-Net이 적용될 수 있다.
본 논문에서 제안하는 3D U-Net 구조의 CNN 모델은 11개 관측소 위치에 해당하는 좌표를 제외한 모든 좌표에서 값이 0으로 마스킹된 (53, 43, 37, 5) 크기의 희소 텐서를 입력받도록 설계되었다.
U-Net은 인코더 단계에서 연속적인 3D 합성곱(convolution) 블록과 다운샘플링(downsampling) 연산을 통해 입력 텐서의 공간적 차원(위도, 경도, 고도)을 점진적으로 줄여나간다. 각 블록은 3×3×3 커널을 갖는 두 개의 3D 합성곱 층, 배치 정규화(batch normalization), 그리고 ReLU 활성화 함수로 구성된다. 다운샘플링은 2×2×2 최대 풀링(max pooling) 연산을 통해 수행되며, 이 과정에서 특징 맵(feature map)의 채널 수는 두 배로 증가한다(32→64→128→256→512). 이러한 구조를 통해, 딥러닝 모델이 초기 레이어에서는 개별 관측소와 그 주변의 기온이나 습도 변화와 같은 국소적인 패턴을 학습하고, 다운샘플링을 거쳐 레이어가 깊어질수록 점차 전체 영역의 정보를 종합하여 한반도 남쪽과 북쪽의 기온 분포의 차이와 같은 거시적인 패턴을 학습할 수 있도록 하였다.
디코더 단계에서는 인코더에서 압축된 저해상도의 특징 맵으로부터 점진적으로 목표 해상도의 대기 상태 맵을 재구성한다. 각 단계에서 특징 맵은 2×2×2 업샘플링(upsampling)을 통해 공간적 해상도가 두 배로 확장되고, 채널 수는 절반으로 감소한다. 업샘플링 이후, 인코더 경로의 동일한 해상도 레벨에서 온 특징맵이 스킵 연결(skip connection)을 통해 현재의 특징 맵과 결합(concatenation)된다. 스킵 연결은 U-Net 구조의 핵심적인 요소로, 다운샘플링 과정에서 손실될 수 있는, 특정 관측소 주변의 미세한 기온 변화와 같은 고해상도의 정밀한 공간 정보를 디코더에 직접 전달하여 최종 재구성의 정확도를 높이고, 깊은 네트워크에서 발생할 수 있는 그래디언트 소실(vanishing gradient) 문제를 완화하여 안정적인 학습을 가능하게 한다. 스킵 연결로 결합된 특징 맵은 인코더와 마찬가지로 두 개의 3×3×3 합성곱 층, 배치 정규화, ReLU 활성화 함수를 거친다. 디코더의 마지막 단계를 거친 특징 맵은 1×1×1 층을 통과하여 최종적으로 5개의 채널을 갖는 (53, 43, 37, 5) 크기의 목표 텐서와 동일한 차원으로 매핑된다.
제안하는 모델은 희소한 입력으로부터 조밀한 3차원 맵을 추정하는 회귀(regression) 문제로 정의된다. 이에 따라 모델의 가중치는 출력 텐서()와 목표 텐서() 간의 차이가 최소화되도록 최적화된다. 이를 위해 손실함수로 평균제곱오차(MSE, mean squared error)를 사용하였다. MSE는 예측 오차의 제곱에 비례하여 큰 오차에 대해 강한 패널티를 부여하며, 경사하강법(gradient descent) 기반 최적화에 효과적인 미분 가능한 함수이다.
5개의 출력 변수(T,z,H,u,v)를 모두 고려한 총 손실함수 L은 각 변수별 MSE의 총합으로 다음의 식 (3)과 같이 정의된다.
이때, c는 5개의 물리 변수 중 하나를 나타내고, Nc는 각 변수의 총 원소수 (53×43×37)를 나타낸다. 와 yc,i는 각각 변수 c의 i번째 격자점에서 모델이 예측한 값과 ERA5 값을 의미한다. 3차원 대기 상태의 재구성을 위한 3D U-Net 모델의 학습은 1980년~2024년 전체 데이터셋 중 80 %인 1980년부터 2015년까지의 315,576개의 데이터를 훈련 세트로, 10 %에 해당하는 2016년부터 2020년 6월까지의 35,432개의 데이터를 검증 세트로 사용하여 진행되었다.
모델의 학습은 PyTorch 2.0 프레임워크를 기반으로 NVIDIA A100 GPU 환경에서 수행되었다. 최적화 알고리즘으로는 대규모 데이터셋으로 수천만 개의 파라미터를 갖는 모델을 학습시킬 때, 각 파라미터마다 학습 속도를 효과적으로 조절하여 빠르고 안정적인 학습이 가능한 Adam 옵티마이저를 사용하였으며, 초기 학습률은 1×10−4로 설정하였다. 검증 손실이 10 에포크(epoch) 동안 개선되지 않을 경우 학습률을 0.5배로 감소시키는 ReduceLROnPlateau 스케줄러를 적용하였고, 30 에포크 동안 개선이 없으면 학습을 조기 종료하였다.
배치 크기는 NVIDIA A100 GPU의 80 GB 메모리와 학습 데이터 규모(315,576개)를 고려하여 결정되었다. 4차원 텐서(53×43×37×5)의 메모리 요구사항과 U-Net의 다중 스케일 특징맵 저장에 필요한 중간 텐서 메모리(약 20 GB)를 분석한 결과, 배치 크기 32가 메모리 효율성과 그래디언트 안정성의 최적 균형점임을 확인하였다. 이 설정은 GPU 메모리의 약 31 %를 활용하여 안정적인 학습을 보장하면서도, 에포크당 9,862회의 그래디언트 업데이트를 통해 충분한 학습 빈도를 제공한다. 모델은 총 200 에포크 동안 학습되었다.
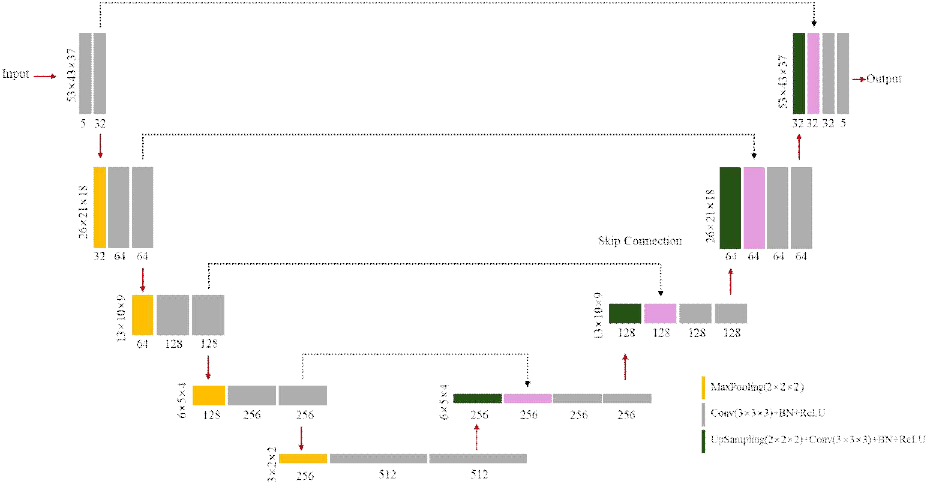
이러한 학습 과정을 거쳐 얻은 최종 모델의 구체적인 구조는 그림 3과 같으며, 총 31,204,357(약 31 M)개의 파라미터를 갖는다. 제안한 모델의 추론 시 메모리 요구량은 약 4 GB로, 모델 파라미터 저장(125 MB), 입력 데이터 처리(1.7 MB), 그리고 순전파 과정의 중간 텐서 연산(약 3.8 GB)을 포함한다. 따라서 전체 대기 상태를 구성하기 위해 고성능 컴퓨팅 환경(수백 GB RAM, 수천 개 CPU 코어)이 요구되는 4D-Var 자료동화 기법과는 다르게, 제안한 모델은 약 4 GB의 메모리와 0.3초의 시간만으로 추론을 완료한다.
학습된 모델의 최종 일반화 성능은 독립적인 테스트 세트(held-out test set)를 통해 정량적으로 평가하였다. 테스트 세트는 훈련 및 검증 과정에서 전혀 사용되지 않은 2020년 7월 1일부터 2024년 12월 31일까지의 데이터(39,480개 샘플, 전체의 약 10 %)로 구성하였으며, 모델 성능은 다음 두 가지 핵심 지표로 평가하였다.
식 (4)는 평균 제곱근 오차(RMSE, root mean square error)를 나타내며, 예측 오차의 크기를 실제 변수의 물리적 단위로 표현하여 모델의 전반적인 정확도를 직관적으로 파악하는 데 사용되는 지표이다. 이때, N은 전체 데이터 포인트 수를, 와 yi는 각각 i번째 격자점에서의 예측값과 ERA5 값을 의미한다.
식 (5)는 피어슨 상관계수(PCC, pearson correlation coefficient)를 나타내며, 예측된 대기 변수들 3차원 공간적 패턴이 실제 ERA5 재분석 자료의 패턴과 얼마나 일치하는지를 나타내는 지표이다. 이때, 와 는 각각 예측값과 실제 ERA5값의 평균을 의미한다. PCC는 −1에서 1 사이의 값을 가지며, 1에 가까울수록 모델이 실제 대기 구조의 공간적 분포를 정확히 재현하는 것으로 해석된다. 이 두 지표를 통해 각 격자점에서의 예측 정확도(RMSE)와 전체적인 패턴의 재현성(PCC)을 종합적으로 평가할 수 있다.
본 논문에서는 컴퓨터 비전 분야의 표준적인 성능 평가 방식을 적용하여, 테스트 세트에 포함된 모든 시점과 모든 격자점에서 제안한 모델의 예측값과 ERA5 재분석 데이터(정답값) 간의 RMSE 및 PCC를 계산하였다[15]. 성능 평가는 5개 기상변수(T, z, H, u, v) 각각에 대해 개별적으로 수행되었다. 구체적으로, 39,480개의 시점과 84,301개의 격자점으로 구성된 총 3,696,441,148개의 데이터 쌍에 대해 성능 평가를 수행하였다.
표 2는 제안하는 모델의 성능 평가 결과를 나타낸다. 5개의 기상 변수 중, 지오포텐셜(PCC 0.858)과 기온(PCC 0.847)이 높은 성능을 보였다. 이는 위도, 고도, 계절 등 거시적인 요인에 의해 그 값이 비교적 완만하게 변하고 국지적 변동성이 낮기 때문이다. 이러한 특성으로 인해 11개 관측점의 데이터만으로도 전체 분포를 비교적 정확하게 추정할 수 있다.
| Variable | Unit | RMSE | PCC |
|---|---|---|---|
| Temperature (T) | K | 2.1 | 0.857 |
| Geopotential (z) | m2/s2 | 380.2 | 0.883 |
| Relative humidity (H) | % | 14.8 | 0.818 |
| Zonal wind (u) | m/s | 3.5 | 0.824 |
| Meridional wind (v) | m/s | 3.2 | 0.848 |
특히, 대기 굴절률 계산의 핵심 변수인 상대습도(PCC 0.824)는 중간 수준의 성능을 보였다[16]. 이는 수증기 분포가 기온 변화, 지형, 해양 등 주변 환경의 미세한 변화에도 민감하게 반응하여 국지적인 변동성이 크기 때문이다. 또한, 상대습도의 RMSE 14.8 %는 주요 기상센터(ECMWF, KMA)에서 운영 중인 수치예보모델의 상대습도 예측 정확도(약 ±15 %)와 유사한 수준으로, 실용적 활용이 가능한 성능을 보였다.
테스트 세트에 대한 평균 PCC는 0.846로, 전통적인 보간 기법(Kriging: PCC 0.75~0.85, IDW: PCC 0.70~0.80)에 비해 우수한 성능을 보였다. 이는 제안한 모델을 통해 예측한 대기 굴절률 분포가 kriging 및 IDW 기법에 비해 신뢰성이 더 높음을 의미한다.
또한, 4D-Var 기반 자료동화기법과 제안한 모델의 예측 성능 비교를 위해, 2024년 12월 1일부터 31일까지 6시간 간격으로 구성된 124개 시점의 데이터를 대상으로, 유럽중기예보센터(ECMWF, European centre for medium-range weather forcasts)의 고해상도 예보 모델 HRES(high resolution forecast)의 초기장(fc0) 데이터와 제안한 모델의 예측 결과를 비교하였다[6],[17]. 비교 결과, 평균 PCC는 HRES fc0이 0.960, 제안한 모델이 0.861로 나타났다.
HRES fc0은 전 지구의 다양한 관측 자료를 4D-Var을 통해 통합하고, 물리 방정식에 기반한 수치예보모델을 통해 대기 상태를 추정한 결과이다. 반면, 제안한 모델은 단 11개 지점의 희소한 관측 자료만을 입력으로 사용하고, 데이터 기반 학습을 통해 전 영역의 대기 상태를 재구성한다. 이와 같은 관측 자료의 양과 수치모델 사용 여부의 차이가 두 모델 간 성능 격차를 야기한 주요 원인으로 해석된다. 한편, 이러한 구조적 차이는 연산 효율성과 적용 가능성 측면에서 제안한 모델에 뚜렷한 이점을 제공한다. HRES fc0을 생성하기 위해서는 고성능 컴퓨팅 자원과 수 시간의 연산이 요구되는 반면, 제안한 모델은 약 0.3초 만에 전체 영역에 대한 대기 상태를 산출하여 높은 연산 효율성을 보인다.
결론적으로, 제안한 모델은 4D-Var 자료동화 시스템에 비해 예측 성능은 다소 낮지만, 전통적인 공간 보간 기법보다는 우수한 성능을 보이는 것으로 나타났다. 따라서 제안하는 모델은 전파 환경의 분포를 실시간으로 추정해야 하는 전파 응용 분야에서 기존 공간 보간 기법을 대체하는 실용적인 대안으로 효과적으로 활용될 수 있다.
그림 4는 2025년 1월 1일 00 UTC에 수집된 11개 관측소 데이터를 입력하여 3D U-Net 기반 딥러닝 모델, Kriging, IDW 세 가지 방법으로 고도 500 m에서 위경도에 따른 기온, 기압, 상대습도 분포를 예측한 결과를 나타낸 것이다. IDW (d)로 예측한 습도 분포에서는 관측소를 중심으로 동심원 형태의 패턴이 형성됨을 확인할 수 있으며, 이는 거리 기반 가중치에 따른 인위적 특성이 반영된 결과로 해석된다. 이러한 분포는 실제 대기의 동역학적 특성을 반영하지 못해, 물리적으로 일관성이 결여된 형태를 보인다. Kriging (c)은 통계적 내삽을 통해 상대적으로 부드러운 결과를 생성하나, 전체적으로 과도하게 평탄화(over-smoothing)된 분포를 보여 대기의 세밀한 구조적 변화를 포착하지 못한다.
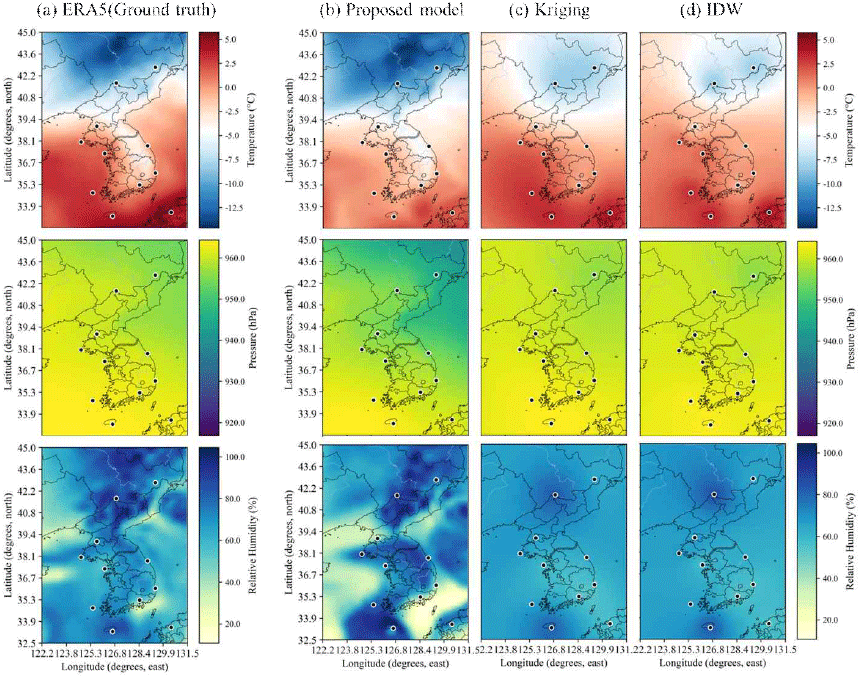
제안하는 모델이 예측한 분포 그림 4(b)는 기온, 기압, 습도에서 모두 그림 4(a)의 ERA5 재분석 데이터와 가장 유사한 공간적 패턴을 보여준다. 특히 그림 4(b)에서 나타난 습도가 높은 영역의 경계와 습도가 낮은 영역의 형태는 그림 4(a)에 나타난 복잡한 습도 분포를 유사하게 재현한다. 특히 습도가 높은 영역과 낮은 영역의 경계에서 Kriging은 현실과 달리 점진적이고 완만한 변화를 보이는 반면, 제안한 모델은 ERA5 재분석 데이터와 유사한 형태로 뚜렷한 경계를 재현한다. 이러한 결과는 전통적인 보간 기법의 한계를 명확히 보여주며, 제안한 딥러닝 모델이 단순한 정량적 지표를 넘어 실제 대기의 물리적 일관성과 공간적 구조를 효과적으로 재현함을 입증한다.
IV. 결 론
본 논문에서는 희소한 라디오존데 관측 데이터로부터 3차원 대기 굴절률을 실시간으로 재구성하기 위한 3D U-Net 기반 딥러닝 모델을 제안하였다. 한반도 및 주변 지역 11개 관측소의 제한된 관측만을 활용하여 한반도 전역의 3차원 대기 상태장을 복원하기 위해, 1980년부터 2024년까지의 ERA5 재분석 자료로부터 총 394,488개의 학습 샘플을 구축하였다. 이러한 데이터셋을 바탕으로 3차원 합성곱 신경망 기반 U-Net 구조를 설계하고, 라디오존데 관측과 전체 대기 분포 사이의 입·출력 관계를 학습하도록 모델을 훈련하였다.
성능 평가 결과, 제안한 모델은 5개 기상 변수에 대해 평균 상관계수 0.846을 기록하여 전통적인 공간 보간 기법보다 우수한 성능을 보였다. 특히 대기 굴절률 계산에서 가장 중요한 변수인 상대습도의 RMSE는 14.8 %로 실용적 허용 기준인 인 ±15 %를 만족하였다. 수증기압이 굴절률 변동의 주요 요인임을 감안하면, 제안한 모델은 한반도 상공의 3차원 대기 굴절률을 예측하는 데 실용적으로 충분한 수준의 정확도를 확보한 것으로 판단된다.
본 연구의 핵심 기여는 복잡한 4D-Var 자료동화를 딥러닝으로 대체하여, 11개의 희소한 관측점(전체의 0.48 %)만으로도 약 0.3초 내에 전체 3차원 대기 상태를 재구성할 수 있게 한 점이다. 이를 통해 연산 시간을 기존 방법 대비 수천 배 단축하면서도 기존의 방법론 대비 향상된 정확도를 갖는 대기 굴절률 모델링을 가능하게 하였다. 이러한 성과는 위성통신, 레이다, 전자전 등 장거리 전자파 전파 해석이 필요한 분야에서 실시간 전파 환경에 대한 실용적인 솔루션을 제공할 것으로 기대된다. 향후에는 물리 정보 신경망(PINN, physics-informed neural networks)을 통해 예측 결과에 물리 법칙을 제약조건으로 부여함으로써, 데이터 기반 모델의 한계를 보완하고 예측 결과의 신뢰도를 확보하는 연구가 필요하다.






