위상 배열 안테나와 다중 사용자 분할 빔포밍을 통한 6G 이동통신과 저궤도 위성 시스템 간 간섭 분석

I. 서 론

위성통신 기술은 지상-위성 통합망 기반의 초공간 연결(hyper-connected) 서비스를 구현할 수 있는 6G 핵심 기술로 주목받고 있다. 최근 통신 장비의 소형화, 발사 비용 절감, 위성 플랫폼의 경량화 등 기술 발전에 따라 저궤도(LEO, low earth orbit) 위성 기반 통신 서비스가 급속히 확대되면서, 지상 6G 통신망과의 융합과 병행 운용 가능성도 높아지고 있다^[1]. 그러나, SpaceX의 Starlink, OneWeb, Amazom의 Kuiper 등은 수천 기의 위성을 운용하는 mega-constellation의 등장으로, 광범위한 지역에서의 동시다발적인 통신을 수행함으로써 기존 지상 통신망과의 간섭 가능성을 크게 높이고 있다. 특히 상향링크(지상→위성)에서 주파수 간섭 문제가 심화되고 있으며, 이는 향후 지상-위성 간 주파수 공유 전략 수립에 있어, 양 시스템 간 간섭을 정량적으로 분석하고 관리하는 것이 핵심 과제로 부각되고 있다^[2].

국제전기통신연합 전파부문(ITU-R)에서 제정한 국제 이동통신(IMT) 중 IMT-2020(5G) 표준화가 완료됨에 따라, IMT-2030(6G) 표준화를 본격 추진하고 있으며, 이를 위해 IMT 시스템의 기술 및 주파수 관련 연구과 표준화 업무를 수행하는 작업반 WP 5D(working party 5D)에서 6G 비전 수립, 기술 요건 정의, 주파수 확보 등을 위한 연구를 진행 중이다. 최근 세계전파통신회의(WRC)에서는 향후 6G 이동통신의 후보 주파수 대역을 4,400~15,350 MHz 범위 내의 총 4개 대역을 선정하고, 위성 기반 서비스와의 주파수 공유 가능성을 검토하기 위해 의제 1.7을 채택하였다^[3]. 이 중 7,125~8,400 MHz 대역은 LEO 위성과 6G 지상망의 기술 수요가 집중되는 전략적 대역으로, 공공 및 민간 활용 가능성 또한 높아 정밀한 간섭 분석이 요구된다. 본 연구에서는 해당 대역을 중심으로, LEO 위성과 IMT-2030 간 간섭 영향을 시뮬레이션 기반으로 분석하고, 해당 대역의 보호 조건을 충족할 수 있는지를 평가하기 위한 간섭 영향 분석을 수행하고자 한다.

기존의 스펙트럼 공유 연구에서는 지상 IMT와 위성 시스템 간의 간섭을 평가하기 위해 이격 거리, 안테나 방향성, 출력제한, 기지국 다양한 배치, 위성의 고도 등 다양한 시뮬레이션 조건을 바탕으로 기술적 요구사항을 분석해 왔다^[4]~[7]. 특히 다중 안테나 배열을 적용한 일부 연구에서는 기존의 IMT 시스템에서 사용하는 능동 안테나 시스템(AAS, active antenna system)을 기반으로 간섭을 분석하였다^[4],[5]. 그러나, IMT-2020 이후 AAS 방사 패턴 모델은 하위 어레이(sub-array) 구조로 확장하는 것을 지원하고 있으며, 이를 통해 더욱 정교한 빔 패턴 제어가 가능해졌지만, 이전의 간섭 분석 모델에는 반영되지 않은 실정이다^[8]. 또한, 여러 사용자 단말(UE, user equipment)에 대해 동시에 다른 데이터를 전송하는 공간 분할 다중 접속(SDMA, spatial division multiple access) 기술 역시 IMT 시스템의 핵심 beamforming(빔포밍) 기법으로, 특정 사용자 방향의 신호를 최적화하고 다른 사용자 방향의 방사선을 억제함으로써 간섭을 줄일 수 있는 장점이 있으나, 기존의 AAS 모델은 이러한 SDMA 기반 디지털 빔포밍 특성을 반영하지 못하고 있어, 실제 시스템의 동작 특성을 충분히 고려하지 못한 한계가 존재한다^[8]. 본 연구는 이러한 한계를 보완한 sub-array 구조와 SDMA 기반 빔포밍 기법을 반영한 확장된 AAS 모델 기반으로 IMT와 LEO 위성 간의 주파수 공유 시나리오에 대한 간섭 분석으로 기존 연구를 확장한다.

본 연구의 시뮬레이션에서 LEO 위성은 간섭을 받는 수신체로서, WRC에서는 실제 운용하는 5~90도 사이의 위성 elevation angle(앙각)을 제안한다^[9]. 위성의 앙각 커버리지 범위 5, 90도를 대표 앙각으로 설정하고, WRC에서 제안하는 위성의 커버리지가 과도하게 축소되지 않는 각으로 25도 앙각을 추가하여 분석을 수행하였다.

본 논문은 LEO 위성 시스템이 상향링크를 수행하는 동안, 지구국(ES, earth station)의 위치를 기준으로 설정된 앙각에 따라 수신 영역 내에 IMT 기지국을 배치하고, 이를 통해 발생하는 누적 간섭을 정량적으로 계산한다. 제 Ⅱ장에서는 간섭 시나리오를 정의하고, 누적 간섭 수식의 파라미터 설명한 뒤, 해당 파라미터들의 적용 방법을 구체적으로 기술한다. 제 Ⅲ장에서는 간섭 시나리오에 대한 시뮬레이션 결과를 분석하고, 마지막으로 제 Ⅳ장에서 본 연구의 결과를 종합하여 해당 대역에서 LEO 위성과 IMT-2030이 동일채널 내에서 공존 가능성을 평가하고 향후 방향에 대해 논의한다.

Ⅱ. 간섭 시나리오

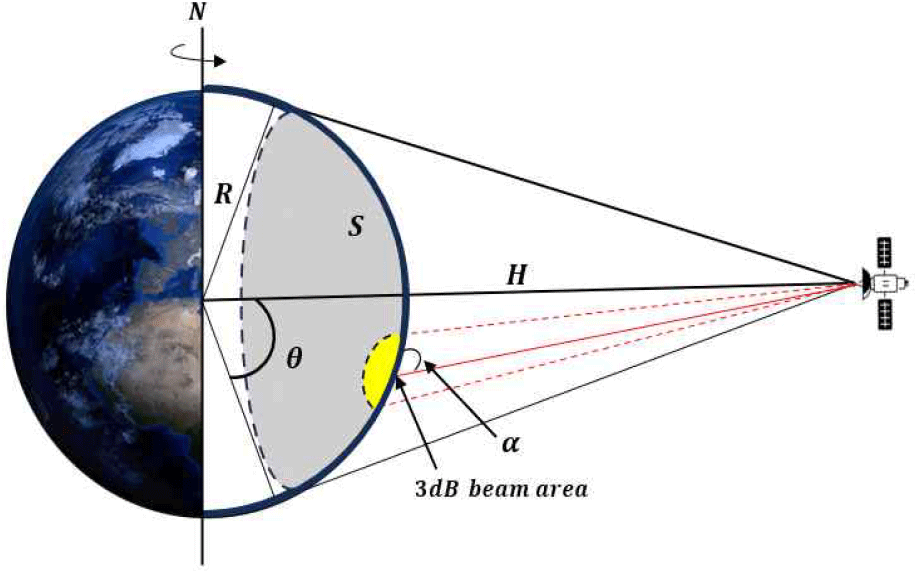
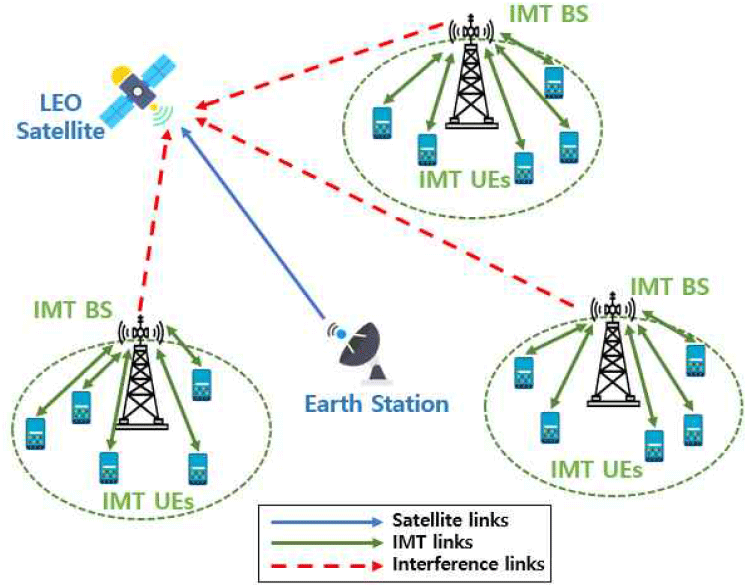
그림 1은 LEO 위성이 지구국(Earth Station) 인근에 배치된 IMT 기지국(IMT BS)으로부터 수신하는 간섭 시나리오를 나타낸다. IMT 기지국은 주변 IMT 사용자 단말(IMT UEs)과의 통신 과정에서 발생하는 전파를 통해 위성에 누적 간섭을 유발하게 된다. 본 연구에서는 시간 기반 Snapshot 시뮬레이션의 각 시간 step j에 대해, 각각의 IMT 기지국 i가 LEO 위성에 주는 누적 간섭 전력 I_agg,j 을 식 (1)과 같이 계산한다.

그림 1. | Fig. 1. LEO 위성과 IMT-2030 간섭 시나리오 | Interference scenario between LEO satellite and IMT-2030.

Download Original Figure

여기서 P_{composite BS}는 IMT 기지국의 유효 등방성 복사 전력(EIRP, effective isotropic radiated power)을 의미한다. G_BS는 IMT 기지국의 송신 안테나 이득으로, 이는 기지국이 바라보는 LEO 위성의 방위각(azimuth) φ과 앙각(elevation) θ, 그리고 셀 반경 내에 분포한 IMT 사용자 단말을 대상으로 수행하는 빔포밍 시의 안테나의 스캔 각(scan angle) φ_scan과 틸트 각(tilt angle) θ_tilt에 의해 결정된다. G_LEO 는 LEO 위성의 수신 안테나 이득으로, 위성의 주 빔(main beam)이 향하는 방향인 지구국과, 분포된 IMT-2030의 기지국 사이의 오프축 각도 ψ(off-axis angle)에 의해 결정된다. PL_total은 간섭 전력에 계산되는 총 경로 손실(path loss)의 합으로, 지역 비율 p와 기지국-위성의 앙각 θ에 의해 결정된다.

2-1 IMT-2030 배치

본 연구에서의 간섭 분석을 위해서는 먼저 위성의 지구국을 중심으로 IMT 기지국을 배치할 수 있는 수신 영역을 계산할 필요가 있으며, 이 영역은 지구국과 위성의 앙각에 따라 달라진다. 그림 2는 위성의 전체 수신 영역을 계산하기 위한 geometry로, 지구의 반지름이 R, 위성의 고도가 H라고 할 때, 위성이 간섭을 수신할 수 있는 전체 영역 S는 식 (2)와 같이 계산할 수 있다^[4].

$$S=2\pi R^2\left(1-\cos \left({\cos }^{-1}\left(\frac{R}{R+H}\right)\right)\right)$$

(2)

그림 2. | Fig. 2. 위성의 전체 수신 영역 | Total receiving area of the satellite.

Download Original Figure

위 식 (2)를 통해, IMT 기지국의 실제 배치 영역 내의 개수는 식 (3)과 같이 정의할 수 있다^[5].

$$N_{IM{T}_{BS}}=S\cdot D_s\cdot R_a\cdot R_b\cdot F_{NL}\cdot F_{TDD}$$

(3)

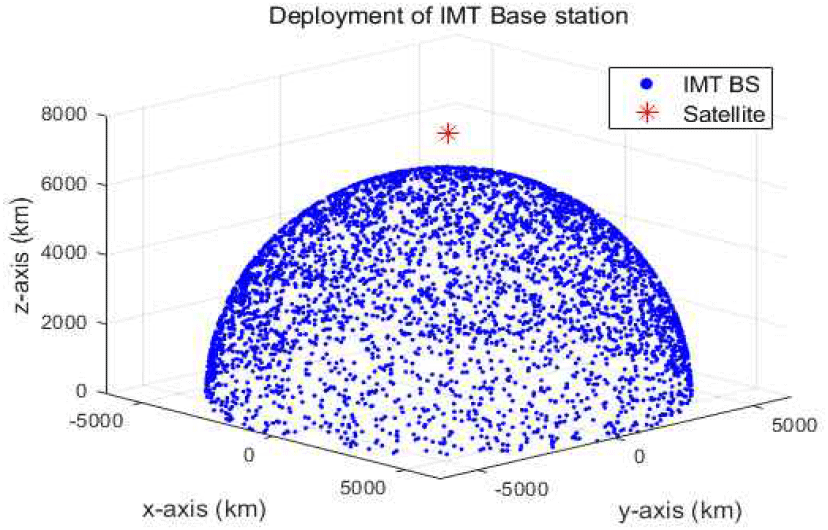
식 (3)에서 S는 LEO 위성의 전체 수신 영역이며, D_s는 단위 면적당 IMT 기지국 밀도를 나타내며 도시, 교외, 농촌 지역(urban, suburban, rural) 등에서 각각 다른 밀도를 제안한다. R_a, R_b는 수신 영역 내에서 거주 지역 비율을 의미한다. F_NL은 network loading을 고려한 실제 활성화된 통신망 비율이며, F_TDD는 시분할 이중화(TDD) 시스템에서 상향링크가 활용되는 시간 비율을 현실적으로 적용함을 의미한다. 그림 3은 그림 2를 기반으로, 식 (2)와 (3)을 통해 위성 커버리지 내에 구면 좌표계 기반으로 균일하게 분포된 IMT 기지국을 나타낸 것이다.

그림 3. | Fig. 3. IMT base station 분포 | Distribution of IMT base station.

Download Original Figure

IMT 사용자 단말의 분포는 IMT 기지국을 중심의 육각형 셀 3 Sector 구조를 따라, 기지국으로부터 최소 35 m 이상 떨어져, 각 섹터의 빔 방향을 기준으로 ±60°에서 레일리 분포로 랜덤하게 배치된다^[10]. WRC-23 결과에 따라, IMT 사용자 단말→FSS 위성 간 간섭은 미미하다고 판단되어, 총 누적 간섭의 간섭원에서 제외하였으며, IMT 기지국의 빔 방향 조정 및 안테나 패턴 형성에 영향을 주는 요소로만 반영한다.

2-2 송신 안테나 이득

2024년 2월 개최된 ITU-R WP 5D 회의에서는, 주파수 공유 및 호환성 연구를 위해 현재 사용 중인 ITU-R Rec. ITU-R M.2101-0에서 제안하는 기지국 AAS의 방사 패턴 모델링에 대한 적절성에 대한 논의가 이루어졌다. 현재 전 세계적으로 C-band(4~8 GHz)에 배치된 IMT 기지국의 AAS는 Rec. ITU-R M.2101-0이 널리 사용되고 있다. 그러나 이 문서에서 제안하는 안테나 모델은 디지털 빔포밍의 특성을 포함하지 않으며, 다중 빔 제어를 더욱 세밀하게 수행할 수 있는 sub-array 구조 또한 고려하지 않는다. 디지털 빔포밍의 핵심 특징은 기지국의 기저대역(baseband) 처리 장치에서 각 빔의 이득과 위상을 조절하여 특정 사용자 방향의 수신 신호를 최대화하는 동시에, 동일하게 스케줄링 된 다른 사용자 방향으로의 방사는 억제하거나 무효화하는 것이다. 이는 SDMA 기술의 일환으로, 최근 IMT 시스템에서 널리 활용되고 있는 기술이다^[8]. 본 연구에서는 기존의 AAS 모델에 sub-array 구조를 확장한 모델과 SDMA 기술이 반영된 디지털 빔포밍 모델의 특징을 분석하고, 두 모델 간의 방사 특성과 누적 간섭 수준을 비교 및 평가한다.

빔포밍은 안테나 배열을 통해 특정 방향으로 전파를 집중하거나 억제하여, 다수의 안테나 소자에서 송수신되는 신호의 위성과 이득을 정밀하게 조절함으로써 원하는 IMT 사용자 단말 방향으로 에너지를 집중시키고, 동시에 불필요한 방향의 간섭을 최소화할 수 있다. Rec. ITU-R M.2101-0의 빔포밍 안테나 모델은 단일 안테나 소자 이득과 다중 안테나 배열 빔포밍 이득의 합으로 계산된다. IMT-2020 시스템에서 사용하는 단일 소자 안테나 패턴은 식 (4)와 같이 계산된다^[11].

$$\begin{array}{l}{A}_E\left(\phi ,\theta \right)\hfill \\ =G_{E,\max }-\min \left\{-\left|A_{E,H}\left(\phi \right)+A_{E,V}\left(\theta \right)\right|,A_m\right\}\hfill \end{array}$$

(4)

여기서 G_{E, max}는 IMT-2020의 최대 안테나 소자 이득이고, A_m은 수평 성분의 안테나 최소 이득을 나타낸다. A_{E, H}(φ)과 A_{E, V}(θ)는 각각 수평 및 수직 방향의 안테나 방사 패턴이며 Rec. ITU-R M.2101-0 문서에 제시되어 있다.^[11]

IMT-2020의 다중 안테나 배열은 N_H×N_V이며, 송신 빔 i에 대한 다중 배열 방사 패턴 A_Beam은 아래의 식 (5)와 같이 계산된다.

$$\begin{array}{l}{A}_{Beam}\left(\phi ,\theta \right)\hfill \\ =A_E\left(\phi ,\theta \right)+10{\log }_{10}\left({\left|{\displaystyle \sum _{m=1}^{N_H}{\displaystyle \sum _{n=1}^{N_V}{W}_{n,m}\cdot V_{n,m}}}\right|}^2\right)\hfill \end{array}$$

(5)

여기서 W_{n, m}은 weighting coefficient로, 특정 방향으로 에너지를 집중시키기 위한 위상 보정 및 정규화를 수행하는 계수이며, V_{n, m}는 superposition vector로, 배열 요소 간의 상대 위치 및 입사각에 따른 위상차를 고려하여 정의되며, 아래와 같은 식 (6) 및 식 (7)을 통해 계산된다.

$$\begin{array}{l}{V}_{n,m}\hfill \\ =\exp \left\{j\cdot 2\pi \left[\begin{array}{l}\left(n-1\right)\cdot \frac{d_v}{\lambda }\cdot \cos \left(\theta \right)\hfill \\ +\left(m-1\right)\cdot \frac{d_H}{\lambda }\cdot \sin \left(\phi \right)\cdot \sin \left(\theta \right)\hfill \end{array}\right]\right\}\hfill \end{array}$$

(6)

$$\begin{array}{l}{W}_{i,n,m}\hfill \\ =\frac{1}{\sqrt{N_H{N}_V}}\times \hfill \\ \exp \left\{j\cdot 2\pi \left[\begin{array}{l}\left(n-1\right)\cdot \frac{d_v}{\lambda }\cdot \sin \left({\theta }_{i,etilt}\right)+\hfill \\ \left(m-1\right)\cdot \frac{d_H}{\lambda }\cdot \cos \left({\theta }_{i,etilt}\right)\cdot \sin \left({\phi }_{i,escan}\right)\hfill \end{array}\right]\right\}\hfill \end{array}$$

(7)

여기서 d_H와 d_V는 각각 수평 및 수직 방향 안테나 요소 간격을 의미하며, 일반적으로 반파장(λ/2) 간격으로 설정한다. m과 n은 각각 수평 및 수직 방향의 안테나 요소 번호를 나타낸다. 배열의 요소 수가 증가할수록 더 정밀한 빔 형성이 가능해지며, 이에 따라 주 빔은 더욱 날카로워져 원하는 사용자 방향의 전력 집중도가 높아지고 side lobe 수준은 감소하게 되어 불필요한 방향의 방사 에너지가 억제되어 간섭을 최소화하게 되는 이점을 가진다. θ_i,etilt와 φ_{i, escan}는 기지국이 랜덤하게 분포된 사용자 단말의 위치를 기반으로 원하는 방향으로의 빔 조정을 위한 scan 및 tilt 각이다.

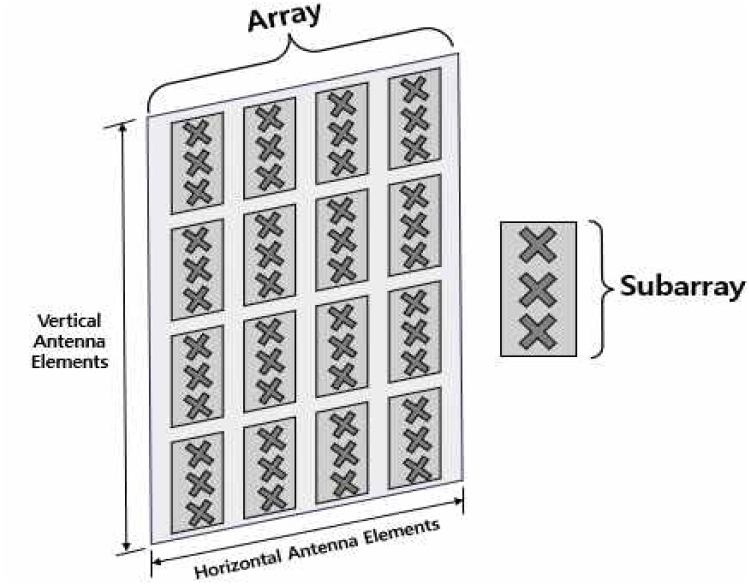
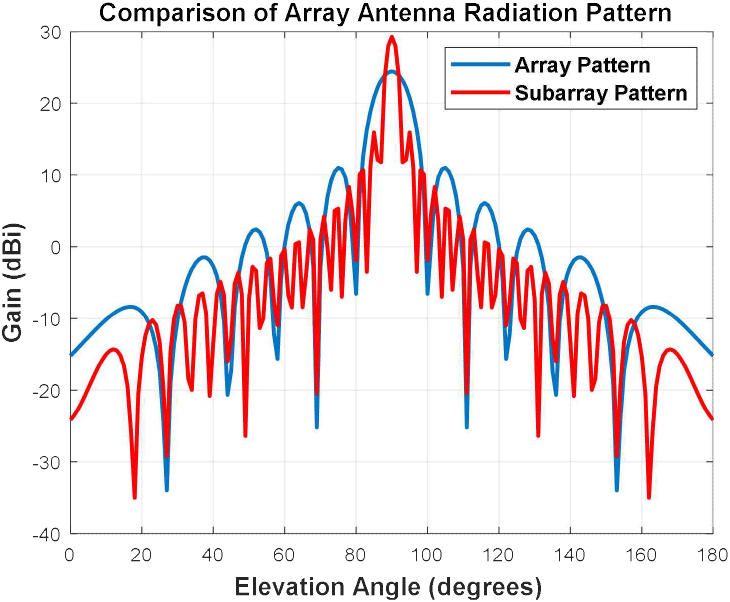
그림 4는 기존의 안테나 배열 구조와 해당 배열을 다수의 소규모 배열로 분할 한 sub-array 배열 구조이다. 배열 구조는 전체 배열을 세분화함으로써 빔 조향의 유연성과 정밀도를 향상시킬 수 있으며, 이를 통해 다수의 사용에 대해 효과적인 빔포밍 제어가 가능해지는 이점이 있다. 또한, 그림 5와 같이 배열의 수가 증가시키면 안테나의 지향성이 더욱 날카로워져, 원하는 방향으로의 에너지를 집중시키는 동시에 불필요한 전파 방향의 이득을 줄여 간섭을 효과적으로 억제할 수 있다.

그림 4. | Fig. 4. 안테나 배열 구조 | Antenna array structure.

Download Original Figure

그림 5. | Fig. 5. 배열 안테나 방사 패턴 비교 | Comparison of array antenna radiation patterns.

Download Original Figure

Sub-array를 통해 확장된 AAS 모델의 방사 패턴은 기존의 AAS 모델의 안테나 방사 패턴을 위한 수식의 A_{E, H}(φ)에 수직 배열 요소의 sub-array excitation 수식을 추가하여 계산된다^[12].

$$\begin{array}{l}{A}_{Beam,sub}\left(\theta ,\phi \right)\hfill \\ =A_{sub}\left(\theta ,\phi \right)+10{\log }_{10}\left({\left|{\displaystyle \sum _{m=1}^{N_H}{\displaystyle \sum _{n=1}^{N_V}{w}_{n,m}\cdot v_{n,m}}}\right|}^2\right)\hfill \end{array}$$

(8)

여기서 A_sub (φ,θ)는 sub-array 방사 패턴이며, 아래의 식 (9)~식 (11)과 같이 계산된다.

$$\begin{array}{l}{A}_{sub}\left(\theta ,\phi \right)\hfill \\ =A_E\left(\theta ,\phi \right)+10{\log }_{10}\left({\left|{\displaystyle \sum _{m=1}^{M_{sub}}{w}_m\cdot v_m}\right|}^2\right)\hfill \end{array}$$

(9)

$$\begin{array}{l}{w}_m=\frac{1}{\sqrt{M_{sub}}}\times \hfill \\ \exp \left(j\cdot 2\pi \cdot \left(m-1\right)\cdot \frac{d_{v,sub}}{\lambda }\cdot \sin \left({\theta }_{subtilt}\right)\right)\hfill \end{array}$$

(10)

$$v_m=\exp \left(j\cdot 2\pi \cdot \left(m-1\right)\cdot \frac{d_{v,sub}}{\lambda }\cdot \cos \left(\theta \right)\right)$$

(11)

여기서 M_sub 은 sub-array 내 요소 개수를 의미하며, d_{v, sub}은 Sub-array 내 수직 요소 간 간격을 의미한다. 그 외의 수식은 기존의 AAS 모델의 수식과 동일하다.

본 연구에서는 WRC-27 회의에서 논의 되었던, Rec. ITU-R M.2101-0 및 WRC-23까지의 관련 연구에서 포함되지 않은 확장된 AAS 모델을 기반으로, 특정 사용자 또는 단말의 위치를 기준으로 신호를 집중하거나 분리하는 공간 분할 다중 접속 SDMA의 핵심 기술 중 하나인 ZF(zero-forcing) 빔포밍 기법을 적용하며 이는 채널의 역행렬을 통해 빔포밍 가중치를 계산함으로써 원하는 사용자에게는 신호를 집중하고 다른 사용자 방향으로는 간섭을 최소화하는 다중 안테나 기법이다^[10].

ZF 빔포밍을 구현하기 위해, 기존의 superposition vector 가중치 V_{n, m}대신, k 번째 IMT 사용자 단말에 대해, UPA(uniform planar array) 계수 행렬 $U_{k_{n,m}}$를 사용하여 채널 역행렬 기반의 빔포밍 가중치를 계산한다^[12].

$$\begin{array}{l}{U}_{k_{n,m}}\hfill \\ =\exp \left\{j\cdot 2\pi \left[\begin{array}{l}\left(n-1\right)\cdot \frac{d_v}{\lambda }\cdot \cos \left({\theta }_k\right)\hfill \\ +\left(m-1\right)\cdot \frac{d_H}{\lambda }\cdot \sin \left({\phi }_k\right)\cdot \sin \left({\theta }_k\right)\hfill \end{array}\right]\right\}\hfill \end{array}$$

(12)

여기서 행렬 $U_{k_{n,m}}$의 크기는 안테나 배열 구성과 동일하게 N_H×N_V 로 설정되며, 송신기 채널의 역행렬 계산은 식 (13) 및 식 (14)와 같이 계산된다.

$$H_k={\left[h_{k,\dots ,}{h}_p\right]}^T$$

(13)

$$W_{k_{ZF}}=H_k^H{\left[H_k{H}_k^H\right]}^{-1}$$

(14)

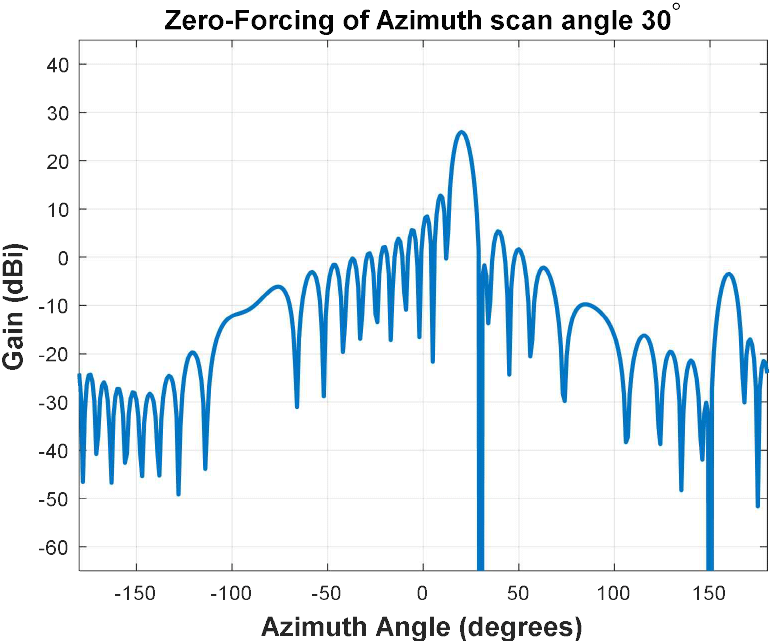
식 (13)의 h_k는 UPA 계수 행렬 $U_{k_{n,m}}$를 벡터화한 결과이며, 행렬 H_k와 켤레 전치 행렬 $H_k^H$를 통해 ZF 빔포밍 가중치 $W_{k_{ZF}}$를 계산할 수 있다. 계산된 $W_{k_{ZF}}$는 확장된 AAS 모델의 빔포밍 가중치 항에 적용되며, 이를 통해 최종적인 ZF 빔포밍 기반의 방사 패턴을 형성할 수 있다. 그림 6에서는 zero-forcing 빔포밍 방사 패턴은 방위각 20° 방향에 위치한 IMT 사용자 단말을 기준으로 통신이 이루어진다고 가정하고, 동시에 스케줄링 되는 IMT 사용자 단말이 방위각 30°에 위치해 있을 때, 해당 방향으로의 안테나 이득에 null을 생성하는 것을 확인할 수 있다. 이와 같이 빔포밍 패턴은 원하는 방향으로의 빔 조정이 가능하며, ZF 빔포밍 기술을 적용하면, 특정 사용자를 향해 에너지를 집중시키는 동시에, 동일한 시간-주파수 자원을 공유하는 다른 사용자 방향으로의 방사는 억제됨으로써 간섭을 크게 완화할 수 있다는 가정이다. 이러한 방사 특성은 WRC-27 회의에서도 스펙트럼 공존 환경에서 간섭 저감을 위한 주요 수단으로 사용될지에 대한 논의가 이루어지고 있다^[13]. 본 연구를 통해 확장된 AAS 모델과 디지털 빔포밍 기술을 추가한 안테나 모델의 비교를 통해 간섭 저감 효과를 분석한다.

그림 6. | Fig. 6. Zero-forcing beamforming 방사 패턴 | Zero-forcing beamforming radiation pattern.

Download Original Figure

Ⅲ. 시뮬레이션 결과

본 논문에서는 앞서 설명한 확장된 AAS 모델과 ZF 빔포밍 기술이 적용된 송신 안테나 모델을 기반으로, IMT-2030 시스템과 LEO 위성 간의 간섭을 정량적으로 분석하고, 두 빔포밍 기술의 간섭 저감 효과를 비교 평가한다. IMT 기지국의 배치 밀도, 안테나 방위각 및 앙각, 지역 커버리지 비율 등 다양한 변수에 대한 몬테카를로 시뮬레이션을 통해 현실적인 간섭 시나리오를 반영하였다. 본 시뮬레이션은 Ⅱ, Ⅲ장에서 정의한 간섭 시나리오와 방법론을 통해, LEO 위성의 상향링크 수신 시 IMT 기지국으로부터 수신 되는 누적 간섭 전력을 분석한다. 시뮬레이션은 고정위성서비스의 파라미터를 선택했으며, 표 1은 IMT-2030, 표 2는 LEO 위성의 파리미터를 보여준다.^{[8]~[10],[16]} 본 논문에서는 IMT 기지국의 커버리지 비율(R_a)과 실제 건물이 존재하는 비율(R_b)에 대한 두 가지 option(#1, #2)을 적용하여 분석을 수행한다. 이 두 계수는 해당 지역 내 IMT 기지국의 수를 결정하는 핵심 파라미터로, 기지국 수는 위성 수신기에 수신되는 누적 간섭 전력을 결정하는 데 있어 매우 중요한 요소로 작용한다. 또한, IMT-2030 기지국으로부터 발생하는 누적 간섭 전력이 계산된 이후, LEO 위성 시스템이 수용할 수 있는 간섭 수준(보호 기준)을 판단하기 위해 간섭 대 잡음 비(INR, interference-to-noise ratio)를 활용하며, 이는 앞의 식 (1)을 포함한 식 (18)과 같이 정의한다.

여기서 I_agg는 누적 간섭 전력이며, N[dB]은 LEO 위성 수신기의 잡음 전력으로 식 (19)과 같이 나타낸다.

잡음 전력 N은 일반적으로 볼츠만 상수 k, 수신 대역폭 BW[Hz], 수신 시스템 온도 T[K]을 의미한다. 이러한 방식으로 계산된 INR 값은 주어진 보호 기준과 비교되어, IMT-2030과 LEO 시스템 간의 동일 주파수 대역에서 발생하는 누적 간섭 수준을 정량적으로 분석하고, 기술별 간섭 완화 성능을 비교하는 데 활용된다.

그림 7은 식 (2) 및 식 (3)를 통해, LEO 위성의 앙각이 각 5°, 25°, 90°일 때 IMT 기지국으로부터의 수신 안테나 이득을 기반으로 한 전체 수신 영역 S의 공간 분포를 실제 지형 데이터를 반영하여 시각화한 것이며, 안테나 패턴에서 주 빔 영역을 기준으로 간섭원을 정의하며, 그 외의 영역은 side lobe, back lobe에 해당하여, 본 연구에서는 수신 영역 내에 −20 dB 영역을 간섭 수신 영역으로 제안한다. 각 시뮬레이션은 해양, 호수, 강 등 비육지 영역을 배제하고 실제 육지 지역에서만 sampling 하는, 가장 worst case의 IMT 기지국 분포를 적용하기 위해 LEO 위성의 주 빔 방향이 서로 다른 지역을 향한다. IMT 기지국의 위치는 전체 수신 영역 내에 통계적 정확성을 확보하기 위해, 랜덤하게 반복되어 결정되는 몬테카를로 시뮬레이션을 적용하였다.

그림 7. | Fig. 7. 위성 수신 안테나 이득 분포 | Satellite receive antenna gain distribution.

Download Original Figure

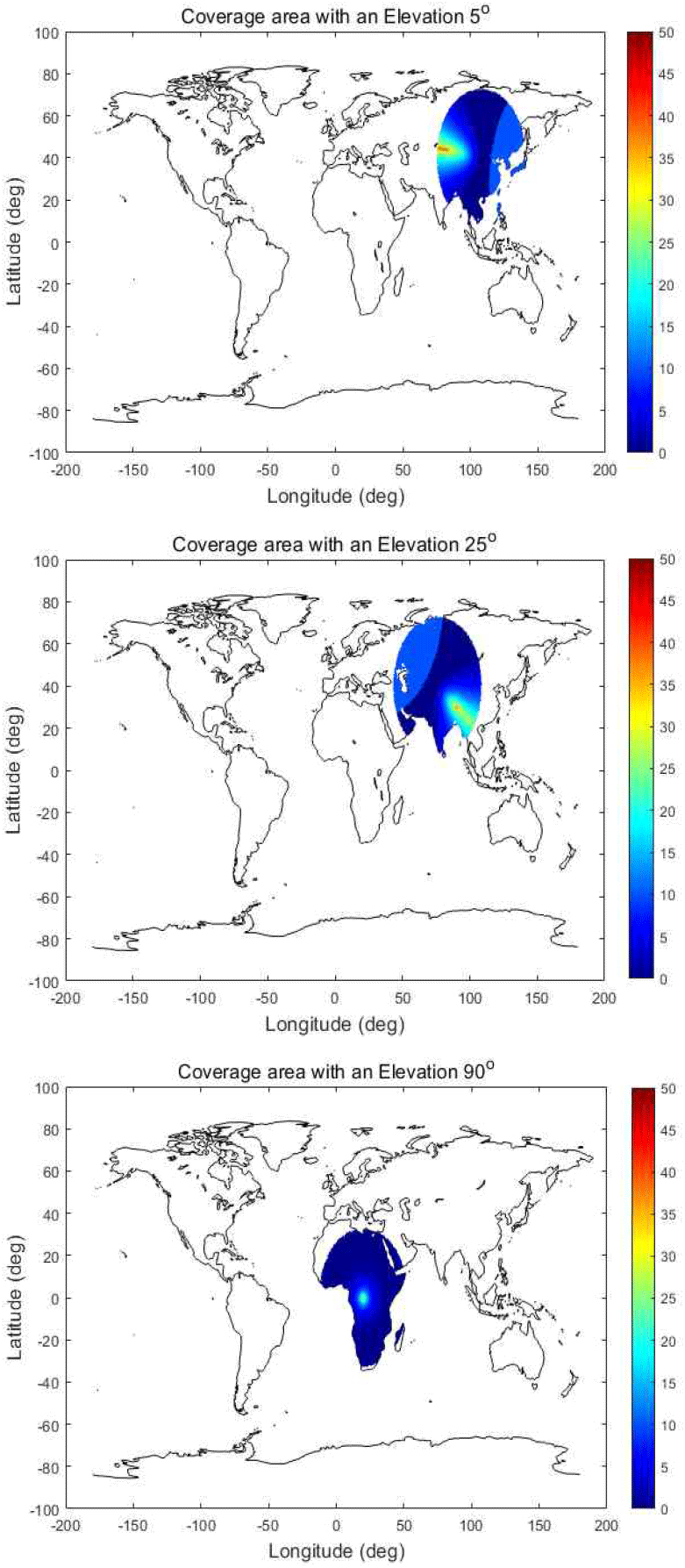
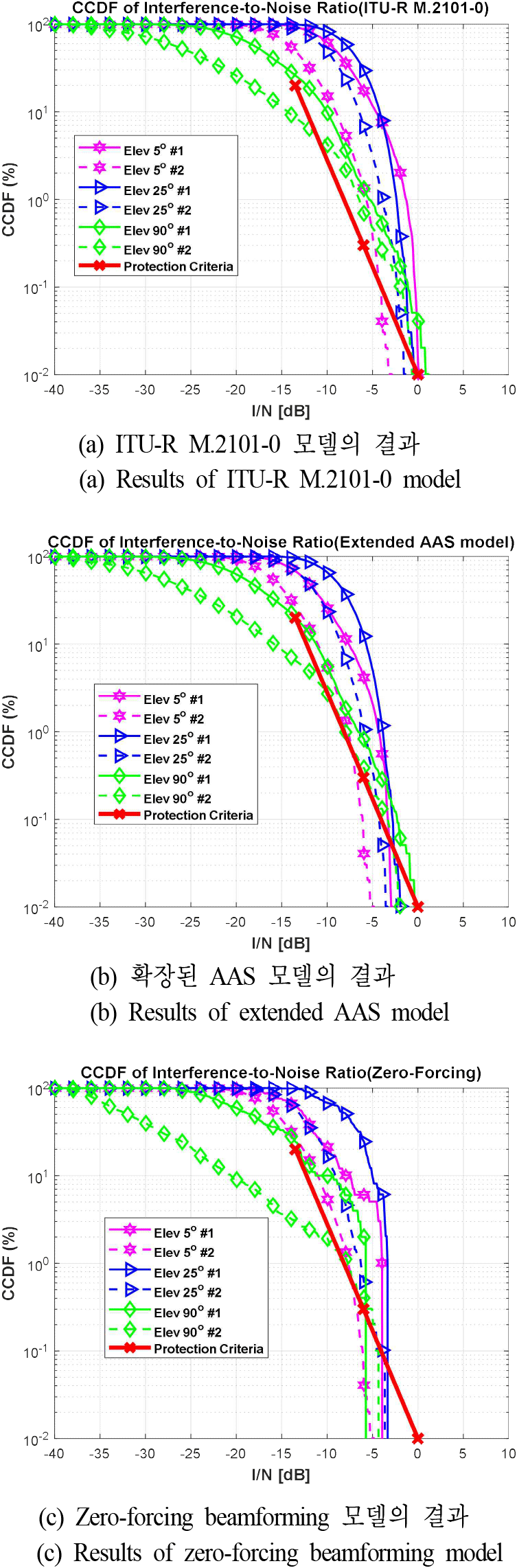
IMT 기지국의 배치를 통한 분석 결과, 위성의 앙각이 낮을수록 3 dB 빔 폭 및 안테나 이득 contour가 넓어져 앙각이 큰 경우보다 더 넓은 지역을 커버하게 되며, 이에 따라 간섭 수신 영역에 포함되는 IMT 기지국의 개수도 증가하게 되는데, 시뮬레이션을 통한 확인 결과, 전체 수신 영역 내 총 IMT 기지국의 개수는 약 1,036,000개일 때, 가장 낮은 앙각인 5°에서 수신 빔 커버리지가 가장 넓기 때문에, 가장 많은 지구국이 포함될 것으로 예상되었으나, 지구의 곡률로 인해 주 빔의 끝부분에 실제 기지국이 배치될 수 있는 지표면 면적이 감소하게 되어 오히려 25°일 때 가장 많은 기지국이 수신 영역에 포함되는 결과를 나타냈다^[17]. 5°와 25°의 경우 간섭 수신 영역에 포함되는 IMT 기지국은 각각 약 13,000~13,500개로 유사하게 나타나지만, 앙각이 90°인 경우 약 800개로 나타난 약 16배의 차이를 보였다. 그림 8은 LEO 위성의 세 가지 앙각 조건(5°, 25°, 90°)에 대해 IMT 기지국의 커버리지 비율과 실제 건물이 존재하는 비율의 두 가지 option에 따른 INR CCDF 결과를 보여준다.

그림 8. | Fig. 8. 시뮬레이션 결과 | Simulation results.

Download Original Figure

본 연구 결과, 모든 경우에서 option #2가 커버리지 비율이 적기 때문에, 배치되는 IMT 기지국의 개수가 적어, option #1보다 간섭 수준이 낮음을 확인할 수 있었다. 전체적인 간섭 분석 결과, 확장형 AAS 모델과 ZF 빔포밍 모델이 기존 ITU-R M.2101-0의 모델과 비교해, 간섭 완화 효과를 보였다. INR 보호 기준을 기준으로, 두 모델 모두 option #2에서 앙각이 90°인 경우, 전체 시간의 20 % 구간에서 보호 기준인 −13.5 dB를 충족했지만, 기지국 커버리지 비율이 높은 #1의 경우는 그렇지 못했다. 또한, 0.3 % 구간에서는 대부분의 앙각에서 간섭 수준이 −6 dB를 초과하는 결과가 나타나, 단기 간섭 영향이 일부 구간에서 존재함을 확인할 수 있었다. 반면, 대부분의 앙각에서는 간섭 수준은 0 dB 이하를 유지하며, 전체 시간의 0.01 % 구간에서 해당 기준을 초과하지 않았다. 아울러, sub-array 구조를 적용한 확장형 AAS 모델과 ZF 빔포밍 기법을 적용한 모델 간의 간섭 저감 성능 차이는 ZF 빔포밍이 특정 방향의 간섭을 억제하는 데 효과적이지만, 위성 방향으로의 null 형성 방향에 포함되지 않는 경우가 많으며, 기지국 밀도가 높은 IMT-2030 환경에서, LEO 위성의 수신 빔 내에 포함되는 간섭원이 광범위하게 분포하므로, 일부 간섭만 제거하더라도 전체 누적 간섭에 미치는 영향이 제한적이다. 확장형 AAS 모델은 주빔 이외의 side lobe 레벨을 전반적으로 낮추는 특성으로 위성이 주 빔 방향에 있지 않더라도, 위성으로 향하는 간섭은 이미 상당히 억제되어 있어, ZF 빔포밍 기법을 적용하더라도, 추가적인 간섭 감소 여지가 크지 않았다. 결론적으로, 두 모델의 간섭 저감 성능 차이는 극히 미미하게 나타났으며, 위성 수신 측면에서의 간섭을 효과적으로 억제하는 데 있어 유사한 수준의 성능을 보였다.

결론적으로, sub-array 구조 기반의 확장형 ASS 모델과 ZF 빔포밍 기법을 적용한 모델 모두 일정 수준의 간섭 효과를 보였으나, 두 모델 간 성능 차이는 크지 않게 나타났다. 결국 ZF 빔포밍은 높은 계산 복잡도와 실제 시스템 구현의 어려움으로 인해, 이와 유사한 수준의 간섭 억제 성능을 보이는 sub-array 기반 빔포밍 모델이 현실적인 대안이 될 수 있음을 시사한다.

Ⅳ. 결 론

본 논문에서는 7,125~8,400 MHz 대역에서 IMT-2030기지국이 LEO 위성에 미치는 상향 링크 간섭을 정량적으로 분석하기 위해, 기존 Rec. ITU-R M.2101-0의 AAS 모델을 기반으로 한 sub-array 구조 확장형 AAS 모델과 ZF 빔포밍 기법을 적용한 모델을 비교 분석하였다. 다양한 앙각 조건(5°, 25°, 90°)과 지형 데이터 기반의 IMT 커버리지 및 도시 밀집도 반영하였으며, 몬테카를로 시뮬레이션을 통해 누전 간섭 전력을 추정하고 LEO 위성 수신기의 간섭 보호 기준과 비교하였다.

시뮬레이션 결과, 두 빔포밍 모델 모두 간섭 저감 효과를 나타냈으며, 일부 앙각에서는 간섭 보호 기준을 충족하였으나, IMT-2030 기지국의 높은 밀도와 LEO 위성의 넓은 커버리지 특성으로 인해 다른 일부 앙각에서는 보호 기준을 초과하는 간섭 수준이 발생하였다. 또한, 확장형 AAS 모델과 ZF 빔포밍 간의 성능 차이는 매우 미미한 수준으로 나타났으며, 이는 ZF 기법의 간섭 억제 효과가 크지 않음을 시사한다. 특히 ZF는 높은 계산 복잡도와 구현의 어려움을 수반하는 반면, sub-array 기반 AAS 모델은 실현 가능성과 복잡도 측면에서 보다 효율적인 대안이 될 수 있음을 확인하였다.

향후 연구에서는 상향링크 간섭 분석뿐 아니라, IMT-2030 기지국으로부터 LEO 지구국이 수신하는 하향링크 간섭 시나리오에 대한 평가가 필요하며, 현재 연구가 LEO 위성을 중심으로 수행된 만큼, 정지궤도(GSO) 위성 시스템을 고려한 간섭 분석 및 비교 연구도 추가적으로 수행될 예정이다.