Ⅰ. 서 론
현대 무기체계 설계에서 레이다 단면적(RCS, radar cross section) 측정은 무기체계의 탐지 가능성을 최소화하고 생존성을 높이기 위한 필수적인 절차로 자리 잡고 있다. RCS는 물체가 레이다에 의해 탐지되는 정도를 나타내는 주요 지표로, 무기체계의 설계 및 성능 평가에 중요한 역할을 한다. 일반적으로 RCS 측정을 위해서는 표적의 크기(D)와 주파수(λ)에 따라 식 (1)의 원전계 조건rFF을 만족해야 하며, 이를 위해서는 큰 시험 공간과 시설이 요구된다[1].
하지만, 이러한 원전계 측정은 현실적으로 많은 비용과 시간이 소요될 뿐 아니라 보안이 중요한 군사 장비의 경우 그 과정에서 추가적인 문제들이 발생할 수 있다. 특히, 대형 시험 시설을 확보하기 어려운 경우나 보안 유지가 중요한 차세대 전투기와 같은 무기체계의 경우, 원전계 RCS 측정을 직접적으로 수행하는 것이 어려워진다. 이러한 제약을 극복하기 위해, 근전계에서 측정한 데이터를 기반으로 원전계 RCS를 예측하는 근전계-원전계 변환(NFFFT, near-field to far-field transformation) 기술 연구가 진행되어왔다[2].
근전계-원전계 변환 알고리즘에는 표적의 산란파 특성을 spherical wave expasion으로 모델링하는 알고리즘인 multi-level SWE-NFFFT[3]와 근전계 데이터를 이용하여 표적의 reflectivity 이미지를 생성하고 이를 바탕으로 RCS를 계산하는 이미지 기반 근전계-원전계 변환 알고리즘[4]~[8], 다중 산란 특성을 가진 표적의 바이스테틱 측정 데이터를 활용해 각 안테나 조건을 원거리장 조건으로 단계적으로 변환하여 RCS를 계산하는 방법[9] 등이 있다. 바이스테틱 측정 데이터 활용 방법과 MSWE 기반 근전계-원전계 알고리즘은 정확도 확보를 위한 최소 샘플수인 truncation number가 크고 모노스태틱 상황에서 행렬 방정식 해의 수렴성 및 정확도가 낮으며 후처리 과정에서 클러터(clutter) 등의 문제를 해결하는데 제약이 있다.
반면, 근전계-원전계 변환 기술 중 이미지 기반 변환(image-based NFFFT) 방식은 이미지 데이터 후처리 기법 적용을 통해 clutter를 제거하여 이미지 해상도를 높임으로써 RCS 계산의 정확도를 개선할 수 있다는 장점이 있다[8].
본 논문은 이러한 이유로 이미지 기반 근전계-원전계 변환 알고리즘을 중심으로 연구를 진행하였다. 하지만 높은 해상도의 이미지를 계산하기 위해서는 많은 수의 근전계 데이터가 필요하며, 이로 인해 측정에 많은 시간이 소요된다는 단점이 있다[10]. 또한, 제한된 샘플 수로 인해 예측 정확도가 떨어질 가능성이 존재한다.
이를 해결하기 위해, 본 논문에서는 기존의 이미지 기반 근전계-원전계 변환 알고리즘에 interpolation을 적용한 알고리즘을 제시한다. 이 알고리즘은 적은 수의 샘플 데이터를 이용하더라도 샘플 수가 많은 경우에 근접하는 높은 정확도의 RCS 계산을 가능하게 하며, 측정시간 또한 단축할 수 있는 장점을 가진다. 본 연구에서는 제안된 알고리즘의 성능을 기존 방법과 비교하여 계산시간과 예측 정확도를 분석하였으며, 그 결과를 통해 알고리즘의 실용성을 평가하였다.
Ⅱ. 이미지 기반 근전계-원전계 변환 알고리즘 분석
이미지 기반 근전계-원전계 변환 알고리즘은 표적의 근전계 산란 데이터를 통해 표적의 산란 중심 분포를 계산하고, 이를 이용해 원전계에서의 RCS를 도출하는 방식이다. 표적에 전파를 입사하면 표면에서 산란파가 발생하며, 이는 전자파의 형태로 방사된다. 이러한 산란파는 표적의 특성에 따라 변하며, 주로 등방성을 가진 산란점들의 집합으로 간주될 수 있다. 이때 표적의 산란분포는 Reflectivity ψ(ρ,φ)로 나타낼 수 있으며, 이를 기반으로 산란 중심 분포를 도출하게 된다[3]. 근전계에서 측정된 산란파는 안테나의 위치와 주파수에 따라 수신되며, 식 (2)와 같이 표적과 안테나 사이의 거리에 따라 수학적으로 표현된다[4],[5]. 여기서 U(k,ϕ0)는 표적의 근전계, 는 focusing operator, ρ0는 표적으로부터 안테나까지의 벡터(scanning area), ρ는 이미지 영역의 벡터, k=2πf/c는 전파상수, ϕ는 방위각을 의미한다.
이 데이터를 활용하여 주파수 영역에서 근전계 데이터를 역변환하고, 이를 통해 산란 중심의 공간적 분포를 도출한다.
Focusing operator는 근전계에서 수신된 산란파를 기반으로, 산란 중심의 위치와 특성을 추정하는 역할을 한다. 이를 통해 표적의 산란 분포를 정밀하게 계산할 수 있으며, 이를 기반으로 원전계에서의 산란 특성을 예측하며 식 (3)과 같이 표현된다[4],[5].
는 근전계에서 원전계로 변환할 때 거리와 위상, 안테나 특성 등을 보정하여 보다 정확한 산란 중심 분포를 계산할 수 있도록 한다. 는 특히 소규모 측정 시설에서의 측정 정확도를 높이는 데 중요한 역할을 하며 식 (4)와 같이 표현된다[4],[5].
이후, 식 (2)~식 (4)를 통해 표현되는 산란분포를 바탕으로 원전계 RCS를 계산하며 식 (5)로 나타낼 수 있다[4].
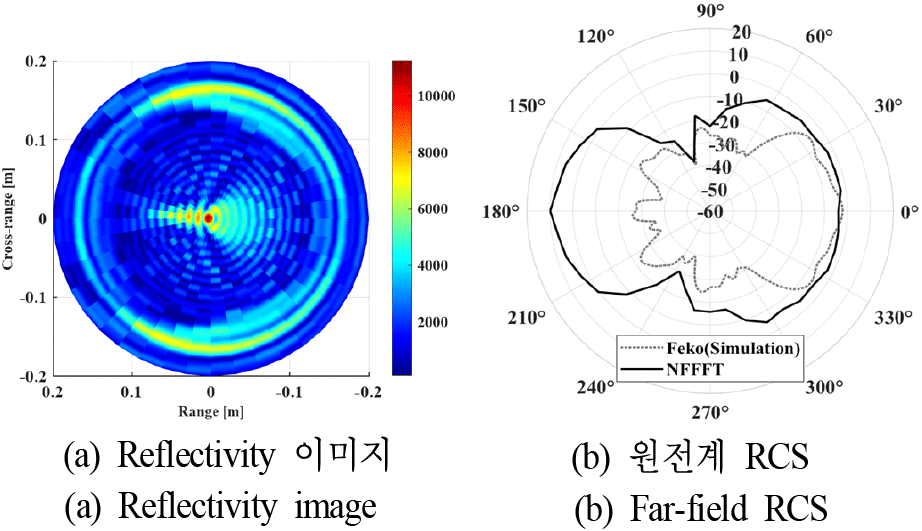
그림 1은 0.17 m 크기의 코너리플렉터를 분석 주파수 6~7 GHz 에서 101개 샘플(중심주파수 6.5 GHz, 대역폭 1 GHz, 주파수 간격 10 MHz)대해 방위각 범위 0°~360°(방위각 간격 9°)로 설정하여 계산한 reflectivity 이미지 결과와 RCS 계산 결과이다. 그림 1에서 확인할 수 있는 것과 같이 이미지 기반 근전계-원전계 변환을 이용하여 RCS 계산할 때, 표적의 측정 데이터 샘플 수가 부족한 경우 RCS 계산 정확도가 낮아진다. 그러나 RCS계산 정확도 향상을 위해 많은 수의 샘플을 확보하기 위해서는 측정시간이 많이 소요되며, 샘플의 수가 증가함에 따라 식 (2)의 reflectivitiy 이미지 계산을 진행하는 과정에서도 계산시간이 기하급수적으로 증가하는 문제점이 발생한다. 이러한 RCS 계산의 정확도와 계산시간 간의 문제를 해결하기 위한 알고리즘에 대해 Ⅲ장에서 그 적용 과정과 조건을 제안한다.
Ⅲ. Interpolation을 적용한 근전계-원전계 변환 알고리즘 및 결과
기존 이미지 기반 근전계-원전계 변환 알고리즘은 표적의 근전계 측정 데이터를 활용해 reflectivity 이미지를 생성하고, 이를 바탕으로 원전계 RCS를 계산하는 과정으로 진행된다. 이 계산과정에서 가장 많은 시간이 소요되는 단계는 근전계 측정 데이터를 사용하여 reflectivity 이미지를 생성하는 단계이다. 전체 계산시간을 단축하기 위해서는 측정 샘플 수를 줄여 reflectivity 이미지를 계산하는 단계에서의 계산량을 줄이는 것이 중요하지만, 샘플 수가 적으면 RCS 계산의 정확도가 떨어지는 한계가 있다.
이러한 문제를 효율적으로 해결하고자 본 논문에서는 reflectivity 이미지 데이터에 interpolation을 적용한 이미지 기반 근전계-원전계 변환 알고리즘을 제안한다.
제안하는 interpolation 적용 이미지 기반 근전계-원전계 변환 알고리즘은 그림 2와 같이 이미지 생성에 필요한 최소 데이터 샘플만으로 이미지를 생성하고, 생성된 이미지에서 RCS를 계산할 때 필요한 추가 샘플은 이미지 데이터 interpolation을 통해 확보함으로써 reflectivitiy 이미지 계산시간 단축과 높은 RCS 계산 정확도를 확보하는 알고리즘이다. 이미지 데이터 구성 과정은 그림 2와 같으며, 본 논문에서는 기존 이미지 데이터의 방위각 영역에서 근접한 두 점의 값을 선형적으로 interpolation 하는 선형 보간(linear interpolation) 방법을 적용하였다. Interpolation이 적용되어 새롭게 구성된 이미지 데이터는 그림 2에 붉은색 점으로 표시된다.
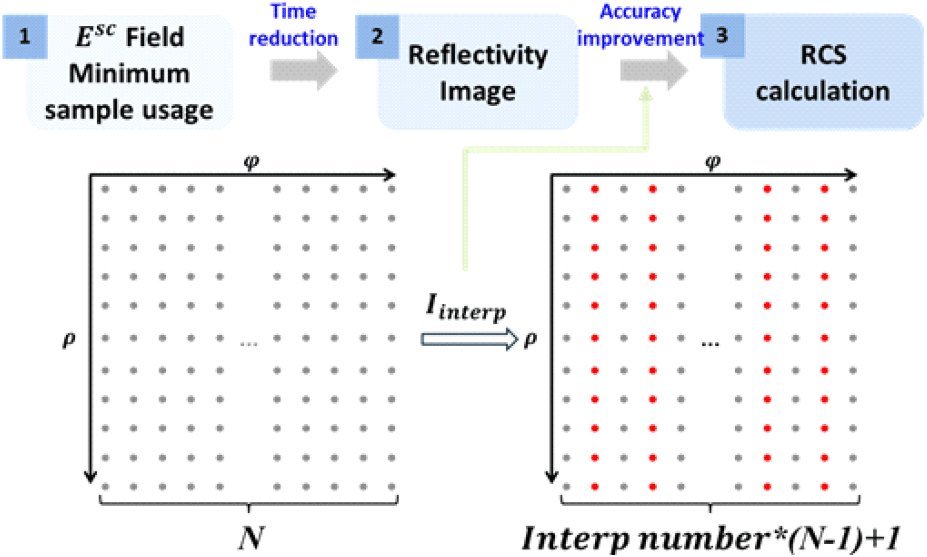
Interpolation을 적용하기 위해서는 이미지 계산 단계에서 aliasing 문제가 발생하지 않도록 Nyquist 조건을 충족해야 한다. Nyquist 조건을 만족하기 위한 방위각 간격 조건(δϕ)은 식 (6)과 같으며[11],[12], 이를 통해 이미지 생성을 위한 최소 샘플 수를 계산할 수 있다.
λ는 파장, Dmax는 물체의 최대 크기를 나타낸다. 그림 3에서 식 (6)의 조건 충족 여부에 따른 재구성된 이미지에서 aliasing 발생 결과를 확인할 수 있다.
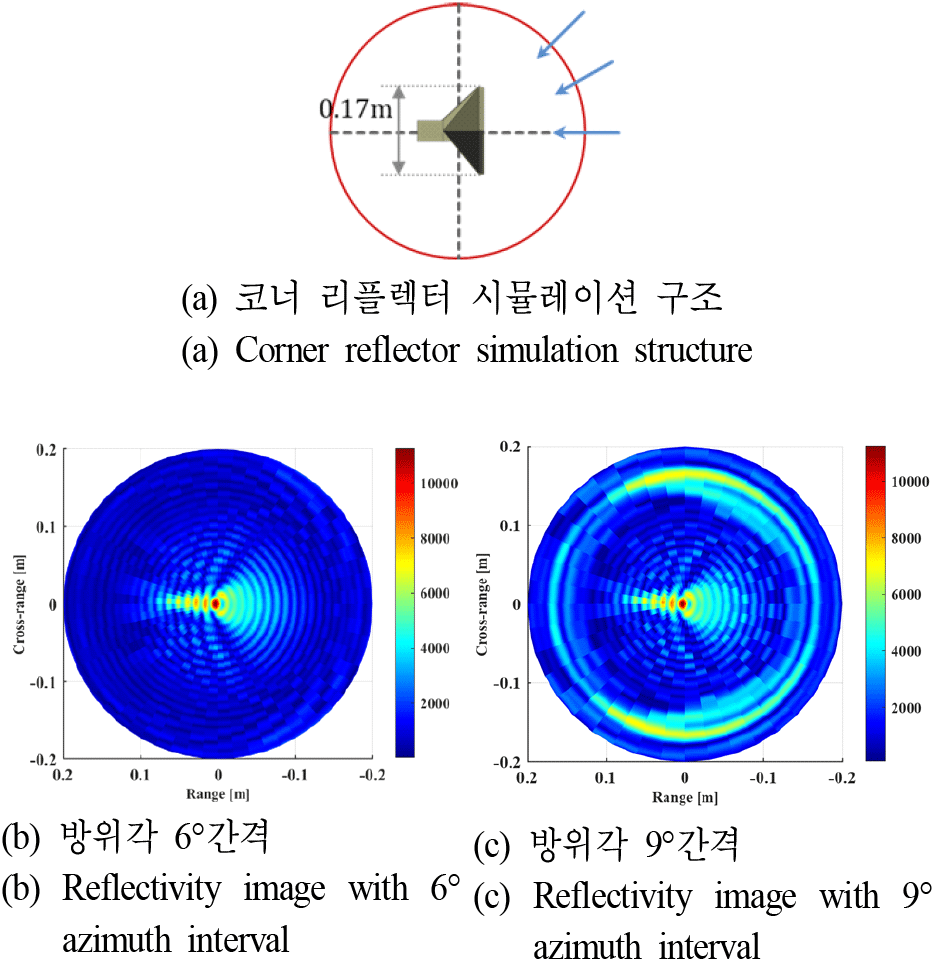
그림 3(a)와 같이 Dmax= 0.17 m인 구조에 대해 식(6) 조건을 이용하여 방위각 간격을 계산하면 7.77°이다. 그림 3(b)에서는 방위각 간격을 6°로 설정하여 조건을 만족시킨 결과, 이미지에서 물체의 형상이 잘 나타나는 것을 확인할 수 있다. 하지만, 그림 3(c)와 같이 방위각 간격을 계산된 조건보다 큰 9°로 설정한 경우 aliasing으로 인해 이미지에서 물체의 형상이 잘 나타나지 않는 것을 확인할 수 있다.
Interpolation 적용 이미지 기반 근전계-원전계 변환 알고리즘의 전체 과정은 그림 4와 같다.
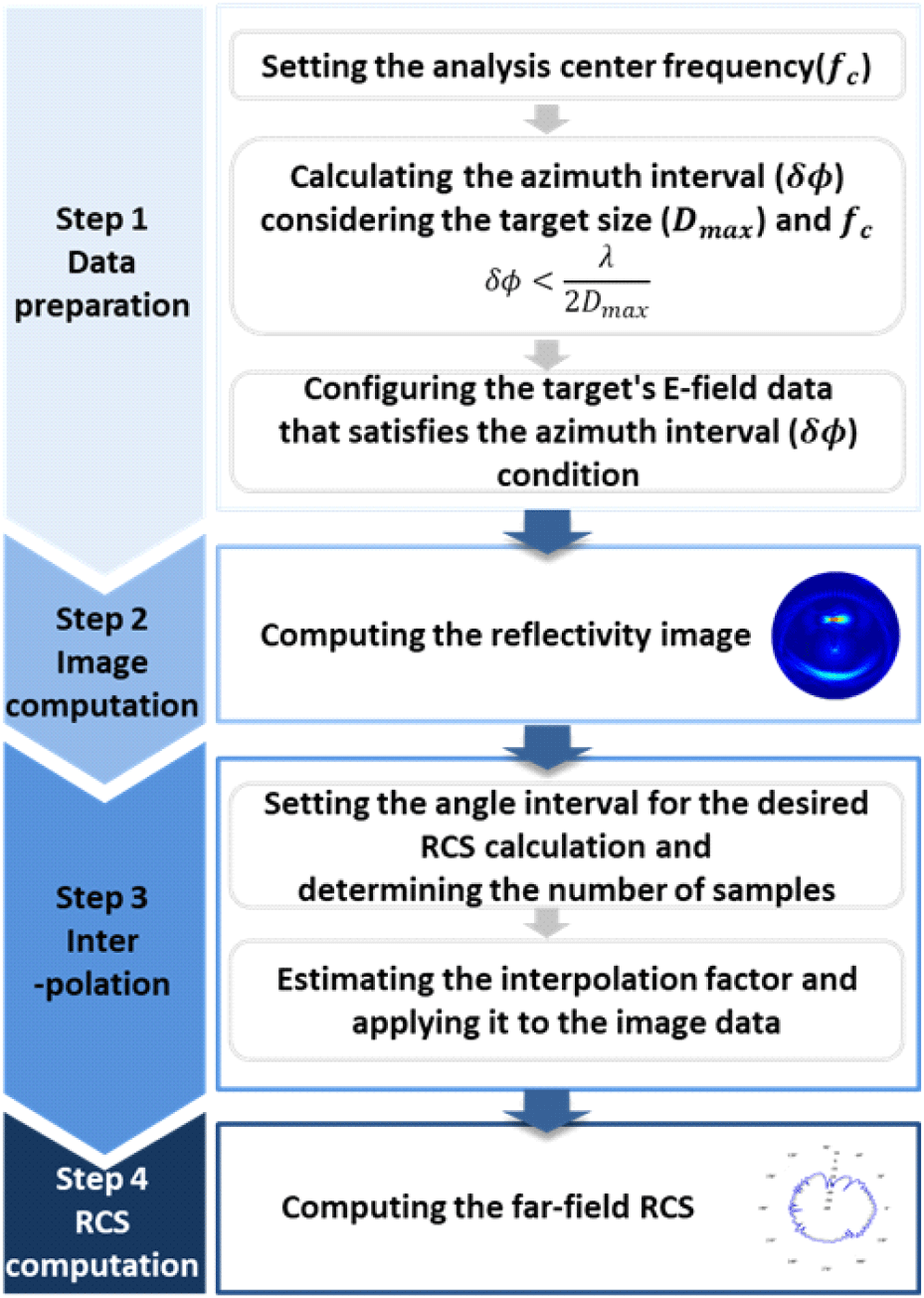
원전계 RCS를 계산하기 위해, 먼저 분석 주파수와 표적의 크기를 고려하여 최대 방위각 간격을 계산하고, 이를 기반으로 표적의 산란장 데이터를 구성한다. 이 산란장 데이터를 활용해 reflectivity 이미지를 생성한 뒤, RCS 계산을 위한 각도 간격을 설정하고, 전체 각도 범위 내에서 필요한 RCS 계산 샘플 수를 산출한다. 그 후, 이미지 데이터의 방위각 샘플 수와 산출된 RCS 샘플 수를 비교하여 적절한 interpolation 배수를 결정한다. 이 Interpolation 배수를 이미지 데이터에 적용함으로써, 추가적인 샘플을 생성하고 이를 통해 RCS 계산의 정확도를 높인다.
3-2장에서는 본 절에서 제안한 알고리즘을 이용하여 코너리플렉터와 구의 복합구조에 대해 원전계 RCS를 계산한 결과를 계산시간과 오차면에서 분석하였다.
Interpolation 적용 이미지 기반 근전계-원전계 변환 알고리즘의 정확도 분석을 위해 그림 5와 같이 코너 리플렉터와 구가 나란히 위치한 복합구조를 이용하여 분석을 진행하였다.
분석 주파수는 6~7 GHz이며 101개 샘플(중심주파수 6.5 GHz, 대역폭 1 GHz, 주파수 간격 10 MHz)에 대해 분석을 진행하였다. 그림 5의 구조에서 물체의 크기인 0.4 m와 식 (6)을 이용하여 계산한 최대 방위각 간격은 3.26°이므로 Nyquist 조건을 고려하여 방위각 간격을 3°로 설정하여 방위각의 범위 0°~360°, 2.4 m의 거리에 대해 산란장 데이터를 구성하였다.
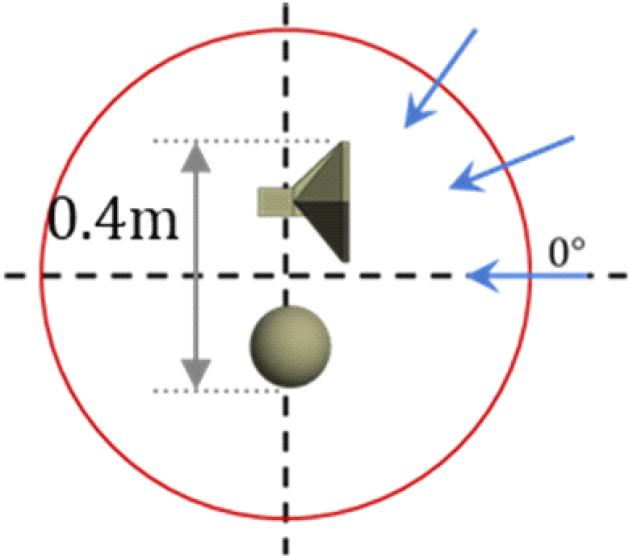
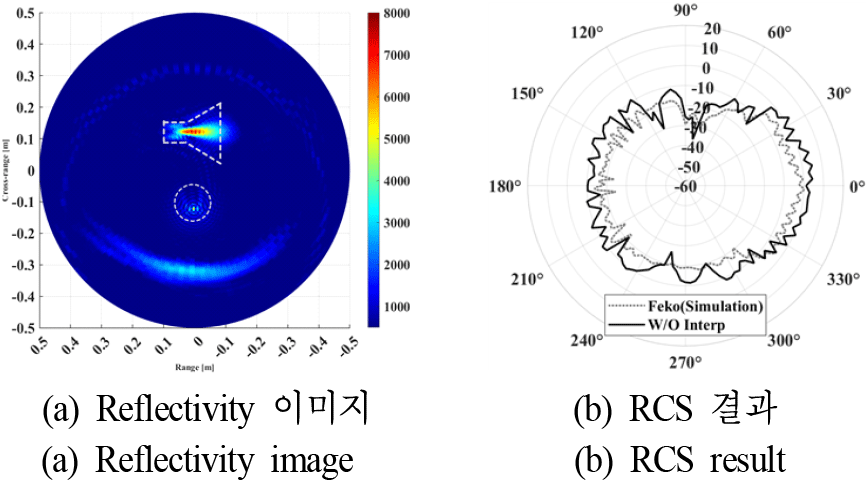
그림 6은 방위각 간격 3°로 설정된 표적의 산란장 데이터를 기반으로 이미지를 계산한 결과와 주파수 6.5 GHz에서의 RCS 계산 결과이다. 표적의 크기와 중심주파수를 고려하여 계산한 식 (6)의 조건을 충족하였기 때문에 이미지상에서 표적의 형태가 잘 나타나는 것을 확인할 수 있다. 한편, RCS 계산은 생성된 이미지에서 거리와 각도로 표현된 모든 픽셀로부터 특정 방위각에 대한 원전계까지의 위상 변화를 고려하여 적분을 수행하는 식 (5)를 통해 이루어진다. 그러나 생성된 이미지는 샘플링 간격과 동일한 3° 간격으로 구성되어 있기 때문에, 각 이미지 픽셀에서의 세밀한 위상 변화를 정확하게 반영하는 데 한계가 존재한다. 이로 인해 그림 6(b)에서 확인할 수 있듯이 RCS 계산 결과와 시뮬레이션 결과 사이에 오차가 발생하게 된다.
위의 계산된 이미지 데이터를 이용하여 방위각 영역 샘플에 대해 2배 interpolation을 적용한 데이터로 구성된 이미지와 RCS 계산 결과는 그림 7과 같다. 그림 6(a) 및 그림 7(a)를 비교하여 보면 interpolation 적용 전과 적용 후 이미지상에서 큰 차이는 없으나, 이미지 데이터 interpolation 적용 후 데이터의 각도 간격이 세밀해짐에 따라 식 (5)를 이용한 RCS 계산 과정에서 reflectivity 이미지에 표현된 산란점의 위상 변화를 정밀하게 반영할 수 있게 됨으로써 그림 6(b)와 그림 7(b)와 같이 RCS 계산 결과에서 정확도가 개선됨을 알 수 있다.
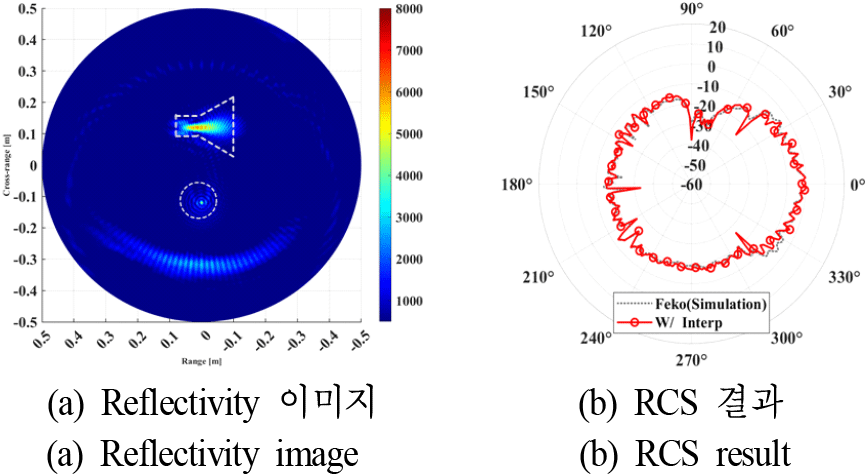
표 1과 그림 8은 각각 방위각 간격 3° 산란장 데이터로 계산된 이미지 데이터에 interpolation 적용 전(Case A)․적용 후(Case B)의 RCS 결과와 방위각 간격 1.5° 산란장 데이터로 계산된 이미지 데이터(Case C)의 RCS 결과와 계산 시간 및 simulation 결과와의 RCS 오차를 비교한 결과이다. RMSE(root mean square error)는 Linear scale로 식 (7)과 같이 표현되는 식을 이용하여 계산 후 dBsm으로 변환하였다.
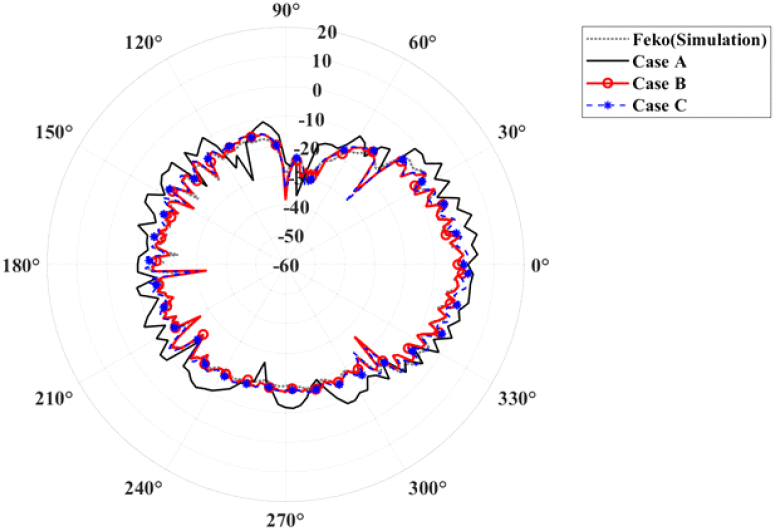
Interpolation 적용 전(Case A)과 적용 후(Case B)의 RCS 계산 결과를 분석한 결과, Case B에서 RMSE가 3.43 dB 감소하여 Case A보다 정확도가 향상됨을 확인할 수 있다. 또한, 계산 시간은 Case B가 262초, Case C가 577초로, interpolation 적용 이미지 기반 근전계-원전계 알고리즘을 활용할 경우 계산 시간을 단축하면서도 정확도를 향상시킬 수 있음을 확인하였다.
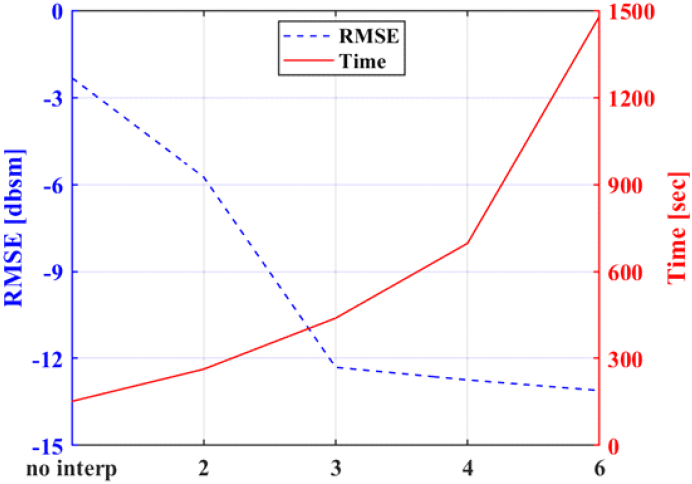
그림 9는 interpolation 배수에 따른 제안하는 알고리즘의 RCS 계산 결과와 시뮬레이션 결과의 종합 오차 변화 및 계산 시간의 추이를 분석한 결과이다. Interpolation 배수를 증가시킬수록 오차가 낮아지는 것을 통해 정확도가 향상됨을 알 수 있으나, interpolation 배수에 비례하여 계산 시간이 증가하기 때문에 계산 시간과 계산하고자 하는 RCS 각도 샘플 수를 고려하여 적절한 interpolation 배수를 조율하여 알고리즘에 적용하여야 한다.
Ⅳ. 결 론
본 논문에서는 기존의 이미지 기반 알고리즘에서 샘플 수 부족으로 인해 발생하는 RCS 정확도 저하 문제와, 샘플 수를 늘리면 계산 시간이 증가하는 상충 관계를 해결하기 위한 interpolation 기법을 적용한 이미지 기반 근전계-원전계 변환 알고리즘을 제안하였다.
전체 계산 과정 중 가장 많은 시간이 소요되는 reflectivity 이미지 계산 단계에서, Nyquist 조건을 활용하여 계산한 최소 샘플 수로 이미지를 구성함으로써 계산 시간을 단축하였다. 또한, 생성된 이미지 데이터에 interpolation을 적용하여 RCS 계산에 필요한 추가 샘플을 확보하고, 이를 통해 RCS 계산의 정확도를 향상시키는 알고리즘을 구현하였다.
제안하는 알고리즘을 통해 계산된 RCS 결과를 시뮬레이션 결과와 비교 분석한 결과, 계산 시간이 단축되고 RCS 계산의 정확도가 향상되었음을 확인하였다.
향후 다양한 interpolation 방법 등을 적용하여 원전계 RCS 계산 정확도를 향상시킬 수 있을 것으로 예상된다.





