Ⅰ. 서 론
유한요소법은 높은 수치 정확도로 복잡한 재료 및 형상을 모델링하는 유용한 접근 방식으로 알려져 있으며, 전자기 문제를 해석하는 데 있어 자주 선택되는 방법 중 하나이다. 그러나 대부분의 전자기 문제는 전기적으로 크고 이에 따라 요소(element)의 수도 늘어나기 때문에, 해결해야 하는 시스템의 차원이 수백만 또는 수십억에 이를 수 있다. 이러한 대규모 전자기 시뮬레이션을 가능하게 하는 방법 중 하나로 영역분할 기반 유한요소해석이 제시되어 있다[1].
영역분할 기법은 전체 에너지 방정식을 각 부영역 에너지 및 부영역 간 경계 에너지의 합으로 정식화하며, 이 기법은 부영역의 독립성으로 인해 병렬 계산에 적극적으로 활용될 수 있다. 이 기법의 예로, 참고문헌 [2]에서는 라그랑주 승수(Lagrange multiplier)를 통해 부영역 간 경계 문제를 정의하는 비중첩(non-overlapping) 영역분할 기법의 일종인 유한 요소 분할 및 합성법(FETI)을 제시하였다[2].
본 논문에서는 헬름홀츠 문제 해결을 위한 두 가지 FETI 기반 영역분할 방법을 소개한다. 첫 번째 방법은 2개의 부영역이 겹치는 경계에서 라그랑주 승수를 사용해 국부 해(local solution)를 결합하는 방법으로, 3개 이상의 부영역이 겹치는 경계는 정의하지 않기 때문에 슬라이스 형태로 영역을 나눠야 한다는 특징이 있으며, dual-version FETI 또는 FETI 방법이라 한다[1],[3]. 두 번째 방법은 3개 이상의 부영역이 겹치는 경계에 추가적인 라그랑주 승수를 할당하여 격자 형태의 영역분할이 가능하며, 이에 따라 더 자유로운 영역분할이 가능하여 가장 선호되는 영역분할 방법의 하나로 FETI-DP 방법이라 한다[1],[3]. 아울러, FETI 방법의 더 빠른 해의 수렴을 위해 부영역 간 경계에 1차 전달 조건을 할당하는 FETI-H 방법에 대해 추가로 논의하였다[4]. 이후, 유한요소법을 사용한 FETI, FETI-DP, FETI-H 방법의 무결성을 완전 도체 큐브의 산란장과 레이다 반사 면적을 통해 검증하며, 마지막으로 FETI-H 기법의 향상된 수렴성에 대해 검증하였다.
앞서 소개된 영역분할 기법들은 기존 연구에서 이미 다루어진 바 있지만, 본 저자들은 이러한 기법들의 타당성 확인 및 알고리듬 습득에 초점을 맞춰 직접 작성한 MATLAB 코드를 사용해 분석을 진행하였다. 또한, 향후 OpenMP 등 CPU 병렬처리나 GPU 병렬처리의 적용을 통해 해석을 더욱 가속화할 수 있을 것으로 예상된다.
Ⅱ. 본 론
본 장에서는 산란체 전자기 해석을 위한 FETI, FETI-DP 방법 알고리즘의 지배방정식 및 적용 방법에 대하여 간략히 요약한다. 이후, FETI 방법을 적용할 때 각 부영역의 경계에 1차 전달 조건을 할당하는 방법(FETI-H)에 대하여 논의한다.
주파수 영역 전자기 산란 문제에서 전기장은 식 (1)과 같은 벡터 헬름홀츠 방정식에 의해 결정된다, 여기서, Esc와 Einc 는 각각 산란, 입사 전기장을 의미한다.
만약에 산란체가 완전 도체(PEC)인 경우, 식 (2)와 같이 공식화될 수 있으며, 도체 표면에서 전기장의 수평(tangential)성분은 존재하지 않기 때문에 디리클레 경계조건()이 부여된다. 여기서, V는 전체 해석 영역이며, S는 해석 영역의 최외각 면을 의미한다.
또한, 식 (2)는 일반화된 변분원리(generalized variational principle)를 적용해 식 (3)과 같이 표현되며, 식 (3)의 각 요소 행렬(elemental matrix)은 식 (4)와 같다. 추후 각 요소들에 대해 합산 과정을 거치게 되면 식 (5)와 같은 행렬 방정식을 얻게 되고, 이 방정식을 풀면 해석구조에 대한 산란 전기장(Esc)을 구할 수 있다. 추가적으로 V에 해당하는 영역은 체적 요소(3차원 벡터 기저 함수 Ne)를 사용하고, S에 해당하는 영역은 표면 요소(2차원 벡터 기저 함수 Ns)를 사용한다.
FETI 방법을 적용하기 위해서는 전체 해석 영역을 각각의 부영역으로 나누어야 하며, 각 부영역들에 대한 초기 행렬 방정식은 다음과 같다[1],[5].
여기서 윗 첨자 s는 부영역을 의미하며, 밑 첨자 b는 부영역에 해당하는 경계, 밑 첨자 i는 경계를 제외한 부영역 성분들이다. 또한, λb는 부영역 간의 경계에 부여되는 라그랑주 승수이며, 부영역에 따라 양과 음의 상반되는 부호를 가지게 된다는 특징이 있다[1],[5].
부영역별 전기장()를 복원하기 위해서는 부영역별로 생성된 행렬 방정식들을 식 (7)과 같이 합쳐 λb를 계산 후, 식 (8)을 사용해 를 복원하며, 마지막으로 식 (9)를 사용해 를 복원한다[1],[5].
여기서 [Bs]는 부영역 내의 경계를 추출하는 Boolean 행렬이며, 부영역에 따라서 양과 음의 부호가 부여된다.
전자기 헬름홀츠 방정식의 영역분할은 부영역 간의 전달 조건 부여 시 더 효율적인 계산이 가능하며, FETI 방법에 1차 전달 조건을 식 (10)과 같이 부여하는 방법을 FETI-H 방법이라 한다[4].
여기서, 1차 전달 조건을 부영역에 부여할 때 [Ms]의 부호는 [Bs]의 부호와 같다.
FETI-DP 방법을 적용하기 위한 초기 행렬 방정식은 다음과 같이 설정할 수 있다[1].
여기서, 윗 첨자 s는 부영역을 의미하며, 밑 첨자 b는 2개의 부영역을 공유하는 경계를, 밑 첨자 c는 3개 이상의 부영역을 공유하는 경계를 의미한다. 마지막으로 밑 첨자 i는 경계를 제외한 부영역 성분들이다[1]. FETI 방법과 유사하게 λb는 부영역 간의 경계에서 상반되는 부호를 가지며, λc는 전부 양의 부호를 갖는다.
부영역별 전기장()를 복원하기 위해서는 부영역별로 생성된 행렬 방정식들을 식 (12)와 같이 합쳐 λb를 계산 후, 식 (13)을 사용해 를 복원하며, 마지막으로 식 (14)를 사용해 를 복원한다[1]. 또한, 부영역별 영향을 합친 행렬([Frr],[Frc],[]) 및 벡터({dr},{})들은 식 (15)와 같이 정의된다.
여기서 [],[]는 각각 부영역 내의 b, c에 해당하는 경계를 추출하는 Boolean 행렬이며, 영역에 따라서 부호가 부여된다.
Ⅲ. 시뮬레이션 결과
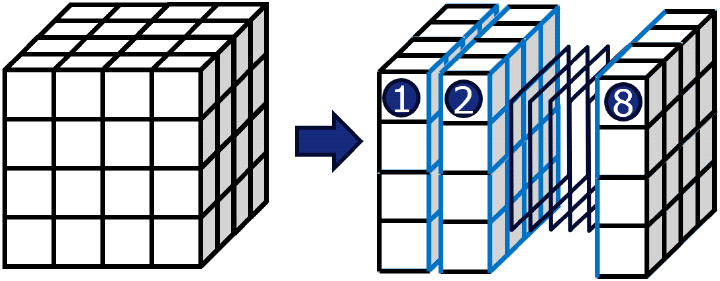
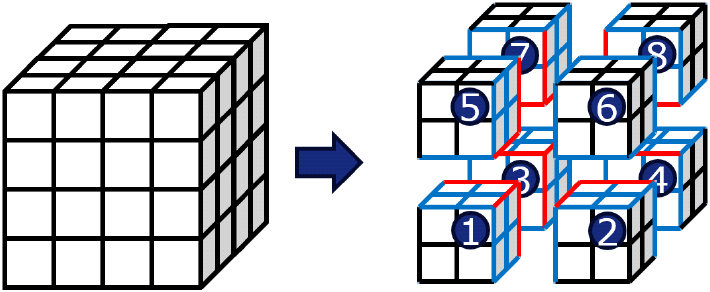
시뮬레이션은 MATLAB 2024a version 환경 그림 1과 같은 구조에 식 (16)과 같은 전자기파가 입사하는 상황에 대해 해석하며, 시뮬레이션 주파수는 300 MHz이다. 또한, 사용한 육면체 요소 개수는 13,824개이며, 45,000개의 요소 모서리(edge)가 생성된다. 아울러, FETI, FETI-DP 적용을 위한 영역분할은 각각 그림 2 및 그림 3과 같이 8개의 영역으로 나누었으며, 부영역 순서대로 부여된 Boolean 행렬의 부호는 각각 (+−+−+−+−), (+−−+−++−)이다. 그림 2 및 그림 3에서 파란색과 빨간색으로 표시된 모서리는 각각 2개, 3개 이상의 부영역 공유하는 경계를 의미한다.
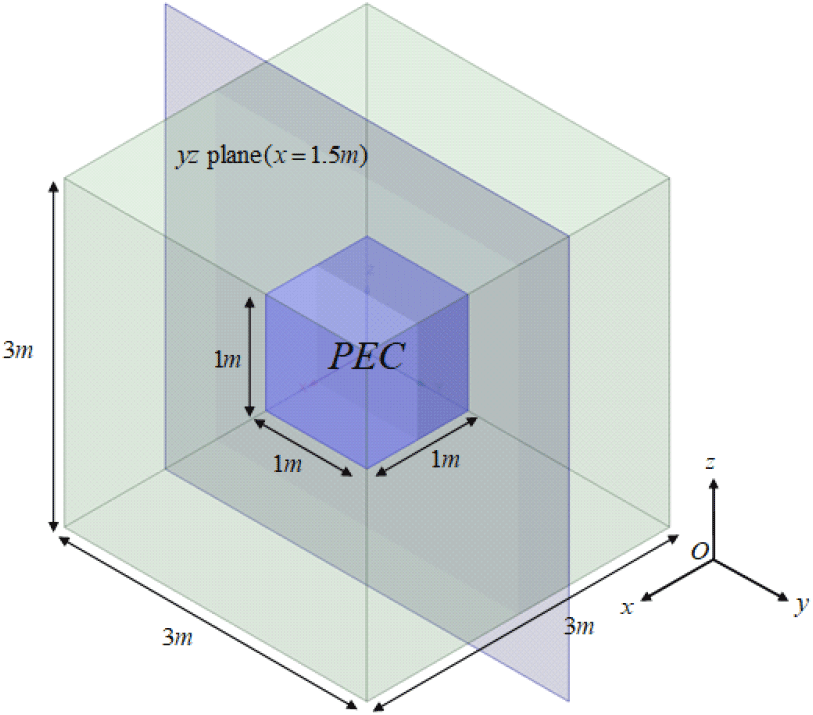
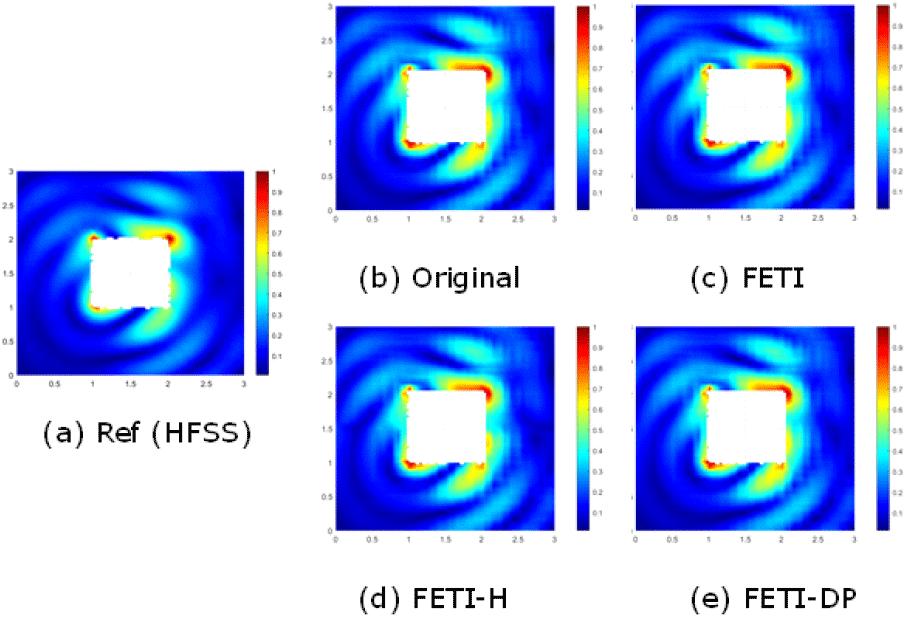
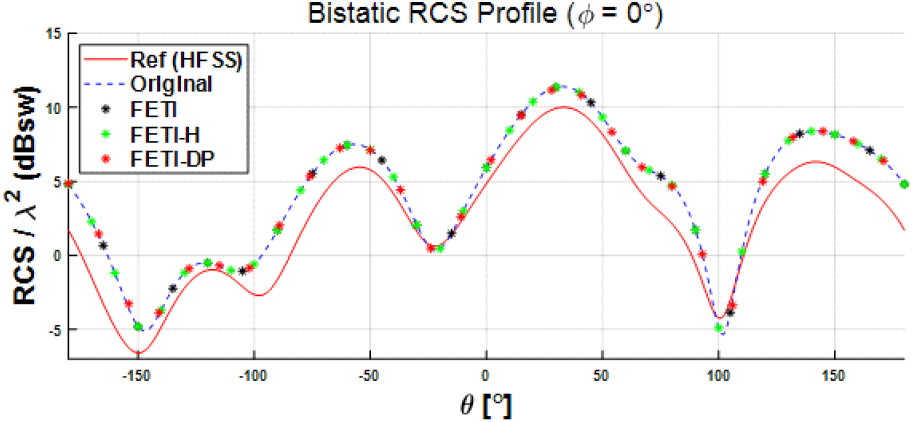
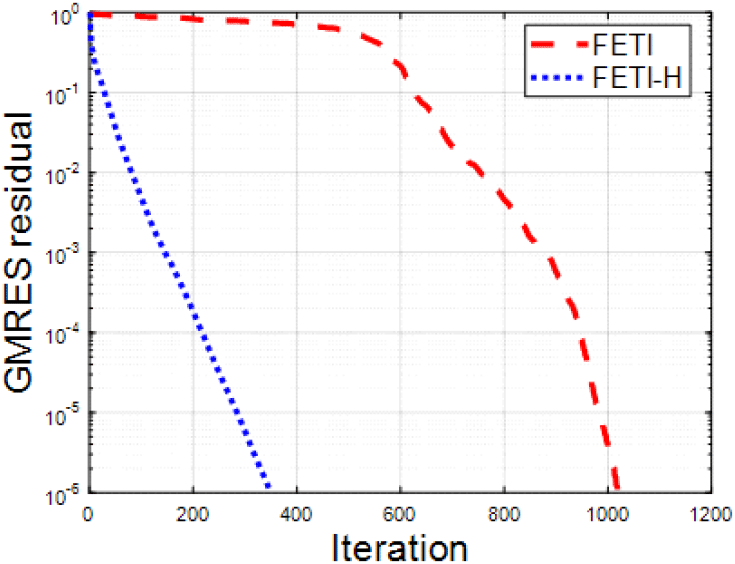
제안한 방법의 정확도 확인을 위해 상용 전자기 해석 소프트웨어인 HFSS를 reference 결과로 사용하며, 식 (5)와 같이 영역분할을 적용하지 않은 행렬 방정식에 대해 MATLAB solver(backslash)를 사용해 얻은 해석 결과(original로 표기)를 추가로 비교한다. 이에 따라, FETI, FETI-H, FETI-DP 방법 결과의 유효성을 그림 1에 표시한 yz 평면(x=1.5 m)에서 산란장 분포(그림 4)와 레이다 반사 면적(그림 5)을 비교 검증하며, 시뮬레이션에서 사용한 MATLAB code는 본 저자들이 직접 전 과정을 작성한 in-house code이다. 또한, FETI, FETI-H의 수렴성 및 해석 속도 비교를 위해 MATLAB 내장 함수인 gmres를 사용하였으며, 허용오차는 1e-6을 사용했다. 그림 6은 반복당 잔차(residual)의 수렴 속도를 비교한 그래프이며, FETI, FETI-H, FETI-DP의 해석 속도는 각각 162 s, 118 s, 111 s로 측정되었다.
Ⅳ. 결 론
본 논문에서는 자체 개발한 FETI 기반 유한요소법을 사용하여 완전 도체 큐브 구조의 전자기 해석을 수행하였으며, 산란장과 레이다 반사 면적에 관한 결과를 도출하였다. FETI, FETI-H, FETI-DP 방법으로 얻은 결과는 영역분할을 적용하지 않은 MATLAB solver의 결과(original)와 일치함을 확인하였고, reference 결과인 HFSS와도 높은 일치도를 보여, FETI 기반 방법으로 얻은 결과의 타당성이 입증됐다. 특히, 부영역 간 경계에 1차 전달 조건을 적용한 FETI-H 방법과 기존 FETI 방법을 비교한 결과, FETI-H 방법이 수렴성과 해석 속도에서 상당한 개선을 보였으며, FETI-DP 방법은 전달 조건을 적용하지 않았음에도 불구하고 FETI-H 방법보다 더 빠른 해석 속도를 보여, 향후 전달 조건 할당을 통해 추가적인 가속화가 가능할 것으로 기대된다. 아울러, 본 논문에서 구현된 높은 정확도를 갖춘 영역분할 방법들은 향후 병렬처리 기법과 결합하여 실제적인 속도 향상과 대형 복잡 구조에 대한 효율적인 해석을 가능하게 할 것으로 사료된다.



