Ⅰ. 서 론
레이다는 전파를 송신하고 표적에 의해 반사되어 수신된 신호를 처리하는 장비로 날씨에 영향이 적고 주·야간에 사용할 수 있어 다양한 분야에서 사용되고 있다. 특히 주변 환경이 복잡해지는 현대 사회에서 고해상도 신호처리 및 다수 표적 탐지는 레이다의 주요 성능 중 하나이다. FMICW(frequency modulated interrupted continuous wave) 시스템은 한 펄스 내에서 주파수 변조를 수행하는 LFM (linear frequency modulation) 파형에 비해 여러 펄스를 사용하는 신호처리 주기 동안 주파수 변조를 연속적으로 수행하므로 광대역 신호 생성이 유리하다. 또한 동일 시점에 송·수신을 하는 FMCW(frequency modulated continuous wave) 시스템과 달리 FMICW 시스템은 송수신 스위칭으로 인해 수신 시간에 송신을 하지 않으므로 수신기를 더욱 민감하게 만들 수 있다. 이에 따라 높은 송신 전력 사용이 가능하므로 레이다의 최대 탐지거리를 늘릴 수 있다[1]. 하지만 송·수신 스위칭은 필연적으로 주기적인 하모닉 주파수 성분을 발생시켜 표적의 탐지 성능이 저하되며 특히 다수 표적 탐지를 어렵게 만든다[2],[3]. 이러한 단점을 해결하기 위해 대역통과필터(BPF)를 사용하여 스위칭 주파수 성분이 없는 영역만 처리하거나 탐지 성능을 높이기 위해 딥러닝을 활용하는 연구들이 이루어지고 있다[3]~[5]. 하지만 대역통과필터를 사용하는 방법은 처리하는 영역에서 주파수 하모닉이 없지만 사용하는 영역을 크게 제한하는 단점을 가진다. 두 번째 기계학습을 활용하는 방법은 대역통과필터를 사용하지 않아 탐지영역의 손실이 없지만 생성된 RD Map(Range-Doppler Map)에서 표적의 개수가 증가하면 탐지 확률이 크게 저하되며, 이를 해결하기 위해 사용된 기계학습은 사전에 많은 데이터 확보와 별도의 학습이 필요하다는 단점을 가지고 있다. 이에 본 논문에는 FMICW 레이다에서 획득된 비트 신호를 거리별로 예상되는 비트 신호와 비교를 통해 RD Map을 생성하고, PRF(pulse repetition frequency)에 의해 나타나는 주기성을 활용하여 다수 표적을 탐지하는 방법을 제안한다.
본 논문의 구성은 다음과 같다. II장에서는 FMCW와 FMICW 시스템을 비교하고 III장에서는 다중 표적 탐지를 위한 FMICW 시스템 구성 방안 및 적용 결과를 상세히 설명한다. 마지막으로 IV장에서는 결론을 제시한다.
Ⅱ. FMCW와 FMICW 시스템 비교
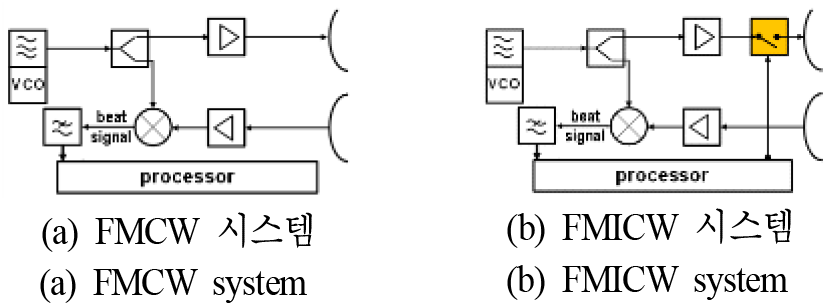
FMICW 시스템은 FMCW 시스템의 단점인 상대적으로 작은 탐지거리를 해결하기 위하여 개발된 시스템이다. 그림 1과 같이 두 시스템 모두 송신 신호와 수신신호가 혼합기(mixer)를 통과한 비트 신호를 사용하며, 가장 큰 차이점은 노란색으로 표현된 스위치의 유무이다.
FMCW 시스템에서 고정된 표적의 비트 신호(Fbeat)는 식 (1)과 같이 정의되며, 이를 통해 표적의 거리를 계산할 수 있다. Ks는 그림 2(a)의 송신 신호의 주파수 변조 기울기, τ는 수신 신호의 왕복 시간, R은 표적과 레이다의 거리, c는 전파의 속도를 의미한다.
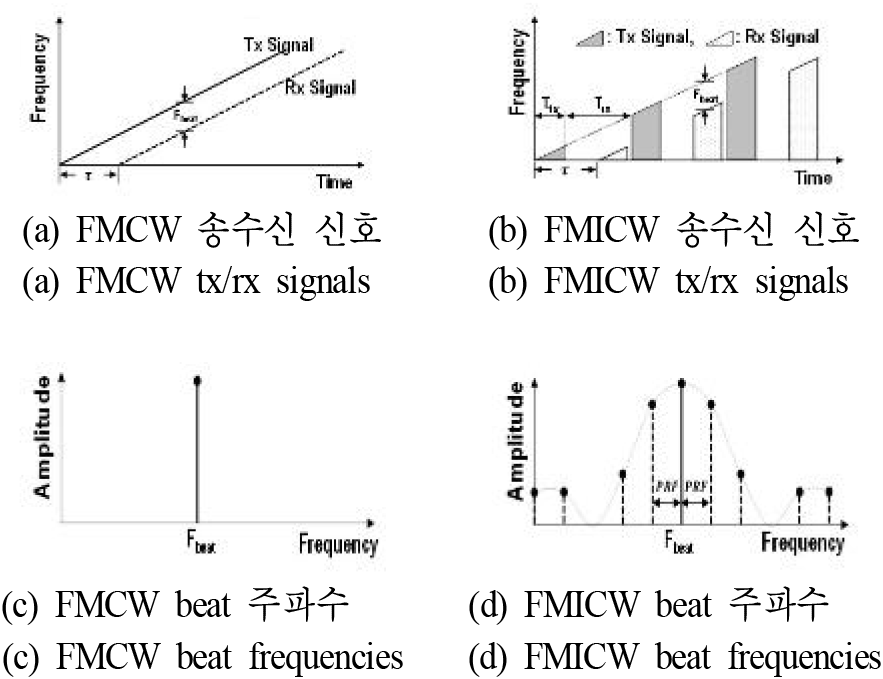
FMICW 시스템은 송수신 스위칭으로 인하여 그림 2(b)와 같이 송신과 수신 시간이 구분된다. 이에 따라 FMICW 시스템은 일반적으로 펄스폭(Ttx)이 증가하면 수신 구간이 감소하여 최소 탐지거리가 제한된다. 또한 송수신 스위칭으로 인하여 그림 2(d)와 같이 Fbeat 신호뿐만 아니라, PRF 주기의 하모닉 주파수가 생성된다. 또한 Fbeat 신호는 거리-도플러 연결(coupling) 효과로 인해 거리와 속도가 함께 영향을 미치므로 2개 이상의 주파수 변조를 사용하여 거리와 속도를 계산한다.
다른 두 시스템의 차이점은 RD Map 생성 방법이다. FMCW 시스템에서는 다수의 스윕(sweep)을 모아 DFT (descret Fourier transform)를 통해 RD Map을 생성할 수 있다. 하지만 FMICW 시스템은 장거리를 위해 사용하므로 탐지거리를 고려하여 일반적으로 FMCW 시스템보다 스윕 시간을 훨씬 길게 설정한다. 이때 시스템에 필요한 속도 해상도 및 범위를 위해 다수의 스윕을 사용하면 RD Map 생성을 위한 시간이 길어져 실제 FMICW 레이다에서는 FMCW와 같은 방법의 RD Map 생성이 제한된다.
Ⅲ. 제안 방법 및 결과
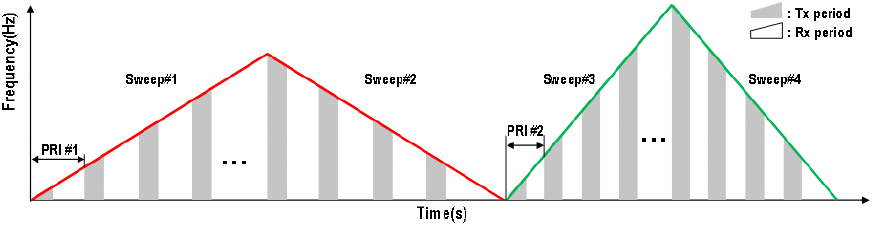
단일 표적에 비해 계산해야 하는 표적의 거리, 속도가 많은 다중 표적은 다양한 주파수 변조가 필요하다. 하지만 다양한 주파수 변조의 사용은 탐지 시간을 증가시키므로 본 연구에서는 그림 3과 같이 4개의 주파수 변조(Sweep#1~4)를 사용하였다. 펄스 주기(PRI)는 Sweep#1과 #2가 동일하며, Sweep#3과 #4가 같다.
RD Map 생성을 위한 가능도(likelihood)를 계산을 위해 식 (2)와 같이 zi를 i번째 스윕에서 측정된 비트 신호의 DFT 값으로 정의하면 거리 r과 속도 v를 가지는 표적의 DFT 패턴 ai(r,v)와 표적의 신호의 크기 값 si의 곱과 잡음 ni의 합으로 표현할 수 있다.
이를 통해 4개 스윕에서의 측정된 비트 신호의 DFT값 z를 식 (3)과 같이 나타낼 수 있다.
식 (3)으로부터 식 (4)와 같이 가능도 L(r,v)을 정의할 수 있다. s는 식 (5)와 같이 추정하여 사용하며, z와 a(r,v)이 유사하면 가능도 값은 증가한다[6].
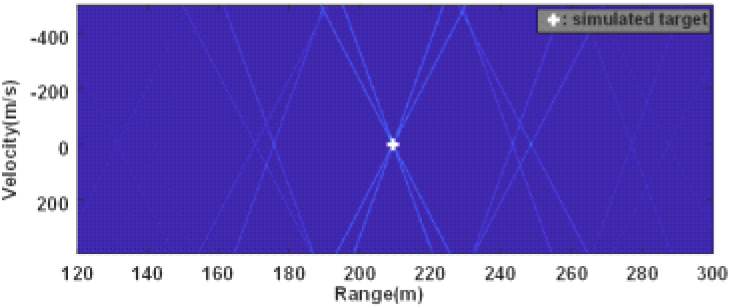
여기에 비트 신호의 거리-속도 커플링 관계를 활용하여 2차원 RD Map을 생성할 수 있다. 생성된 RD Map에는 거리-속도 커플링과 PRF 하모닉 신호로 인하여 그림 4와 같이 다수의 직선이 생성된다[6].
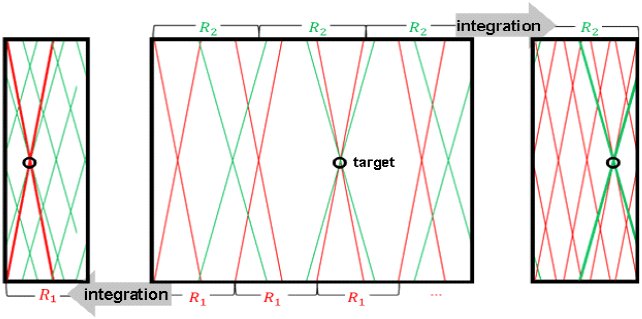
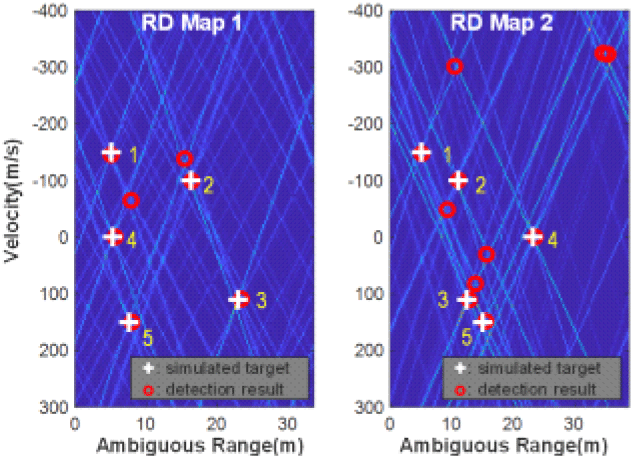
이는 다른 주파수 기울기와 PRF를 사용하여 비트 신호가 특정 거리, 속도에 매칭될 가능도를 계산한 RD Map의 특징으로 일반적인 CFAR(constant false alarm rate)로는 탐지가 어렵다. RD Map에는 스윕 개수와 같이 4개의 다른 기울기의 직선이 생성되며 표적은 4개 직선의 교점에 위치하게 된다. 표적 탐지를 위해 RD Map에서 허프 변환(Hough transform)을 활용해 직선을 찾고 이를 통해 교점을 계산할 수 있다. 여기서 허프 변환은 이미지에서 직선을 찾는 알고리즘이며 이미지 내의 어떤 점이라도 선 집합의 일부일 수 있다는 가정하에 직선의 방정식을 이용해 직선을 검출하는 알고리즘이다[7]. 하지만 RD Map의 모든 영역에서 직선 검출 및 교점 계산은 연산량이 많고, 작은 신호는 탐지하기 어렵다는 단점이 있다[3]. 이를 해결하기 위해 그림 5와 같이 생성된 RD Map의 주기성을 사용하여 일정 간격으로 누적할 수 있다. 거리(R1, R2)의 범위로 누적된 RD Map은 각각의 연관있는 직선들이 누적되어 신호의 크기가 커진다.
본 연구에서는 2개의 PRF를 사용하였으며 주기(R1, R2)는 식 (6) 및 식 (7)과 같이 계산된다. 여기서 c는 전파의 속도, Ks1, Ks2는 그림 3의 Sweep#1~2와 Sweep#3~4의 주파수 변조 기울기를 의미한다.
누적된 작은 크기의 RD Map에서 직선을 찾아 교점을 계산하면 모호성을 가진 거리의 표적을 찾을 수 있다. 이후 2개의 PRF의 주기성을 고려하여 모호성을 해결하면 표적의 실제 거리를 계산할 수 있다.
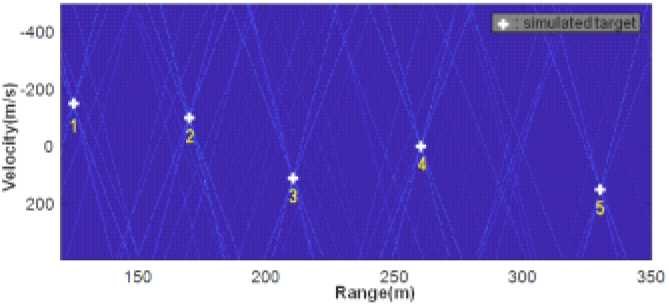
알고리즘의 효과를 검증하기 위해 SNR 20dB의 5개 표적을 생성 후 탐지 결과를 확인하였다. 5개 표적의 RD Map은 그림 6과 같다. 시스템에서 적용한 PRF 2개를 고려하여 모호성을 가진 거리(R1, R2)로 각각 누적하면 그림 7에서 RD Map 1과 2의 작은 크기의 RD Map을 생성할 수 있다. 생성된 2개의 RD Map에서 교점을 찾으면 적색 원과 같이 실제 표적의 개수보다 많은 수가 탐지된다. 탐지된 표적 중 같은 속도의 표적을 찾으면 모사된 표적과 같은 5개의 표적만 정확하게 탐지할 수 있다.
이후 모호성을 가진 거리(R1, R2)과 최대 탐지거리를 고려하여 모호성이 없는 실제 표적의 거리를 최종적으로 계산할 수 있다. 표 1은 모사된 5개 표적의 거리, 속도 및 탐지 결과를 나타낸다. 5개 표적 모두 거리와 속도를 정확하게 계산함을 알 수 있다.