Ⅰ. 서 론
장거리 환경에서 레이다의 성능을 정확하게 평가하고 운용하기 위해서는 안테나의 복사 패턴 및 전파 특성이 고려된 정확한 전파 해석 기반의 탐지거리 예측이 필요하다. 기존 상용 전자파 해석 프로그램을 이용한 탐지거리 예측 방법은 안테나 복사 패턴을 정확하게 반영하지만, 대기 굴절률에 따른 전파 굴절 현상을 고려하지 못하는 한계가 존재하였다[1]. 포물형 방정식 기법 기반 방식은 대기 굴절률과 지구 곡률을 효과적으로 반영하여 장거리 전자파 해석 방법으로 적합하다[2]. 하지만, 해석 과정에서 안테나 복사 패턴을 정규화된(normalized) 단일 가우시안 빔 패턴을 이용하여 초기 전기장 세기를 구하므로 경로 손실 및 수신 전력 계산 시 복잡한 안테나 패턴 및 이득을 고려하지 못하는 한계가 존재하였다[3]. 실제 장거리 레이다는 위상 배열 안테나를 사용하여 주엽과 여러 개의 측엽을 가지는 복잡한 복사 패턴을 가지며, 높은 안테나 이득을 가진다[4]. 따라서, 정확한 레이다 탐지거리 분석을 위해서는 실제 안테나 복사 패턴의 고려가 필요하다.
본 논문에서는 경계조건을 PEC(perfect electric conductor)로 해석하는 split-step Fourier transform 기반의 포물형 방정식 기법(SSPE)를 활용하여, 안테나 복사 패턴을 고려한 레이다 탐지거리 분석 방법을 제안한다. 제안된 방법은 임의의 레이다 단면적 (RCS, radar cross section)을 가지는 표적에 대해 대기 굴절률에 따른 자유 공간과 덕트 현상 발생 시의 레이다 수신 전력을 계산하여 레이다 탐지거리를 분석한다.
Ⅱ. 본 론
포물형 방정식 기법의 초기 필드 값은 다음과 같이 파수(wavenumber) 도메인에서 안테나 고도각을 고려한 단일 가우시안 빔으로 정의된다[5].
k0: 자유 공간 파수, θbw:−3 dB빔폭, θelv: 안테나 고도각
식 (1)로 정의된 패턴은 파수 도메인에서 최댓값 1을 가지는 정규화된 패턴이다. SSPE 방법은 식 (1)에서 계산된 패턴을 안테나 고도 xs에 대해서 다음과 같이 파수 도메인 초기 필드 u(0,kx)연산에 적용한다.
이러한 방법으로 계산한 파수 도메인에서의 초기 필드 값을 역 푸리에 변환하여 수직 방향 공간 도메인에서의 초기 필드 값으로 변환한다. 수직 방향 공간 도메인 변수는 x로 고도를 의미하며 수평 방향 공간 도메인 변수는 z로 거리이다. 위와 같이 정규화된 단일 가우시안 빔을 안테나 패턴으로 사용한 경우, 다음의 식을 통해 보어사이트 방향 경로 손실을 계산할 수 있다[6]. PL(path loss)는 경로 손실, FSPL(free space path loss)는 자유 공간 경로 손실, PF(propagation factor)는 전파 계수이다.
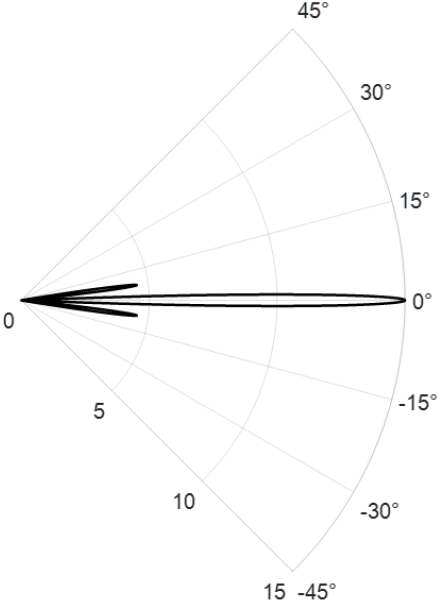
포물형 방정식 기법으로 계산된 경로 손실은 안테나 보어사이트 방향으로 자유 공간 경로 손실과 같은 값을 가져 기존의 SSPE 방식의 가우시안 빔은 최대 0 dBi의 이득을 가지는 빔 패턴임을 알 수 있다. 하지만 실제 장거리 레이다의 경우, 위상 배열 안테나를 사용하여 주엽과 여러 개의 측엽, 높은 이득 등을 가지는 경우가 많아, 실제 장거리 레이다의 탐지거리를 분석하기 위해서는 위의 여러 요소들을 모두 고려하여야 한다. 본 논문에서는 그림 1과 같은 측엽, 이득이 존재하는 안테나 복사 패턴을 SSPE 방법에 적용하였다. 그림 1의 안테나는 1개의 주엽과 2개의 측엽을 가지며, 최대 이득 15 dBi를 가진다. 주엽과 측엽의 이득은 단일 가우시안 빔인 식 (1)에 각 엽의 이득에 해당하는 계수를 곱하여 반영하였고 측엽의 고도각은 식 (1)의 고도각에 해당하는 변수인 θelv에 측엽의 고도각을 더하여 주엽 1개, 측엽 2개를 구성하였다. 그 후, 식 (6)과 같이 고도각에 따라 최대값을 가지는 값을 선택하여 그림 1과 같은 패턴을 만들었다.
주엽의 이득 및 −3 dB 빔폭이 각각 15 dBi, 2°이며, 측엽은 각각 4.55 dBi, 3°의 이득과 빔 폭을 가진다. 측엽의 고도각은 ±7.5°이다.
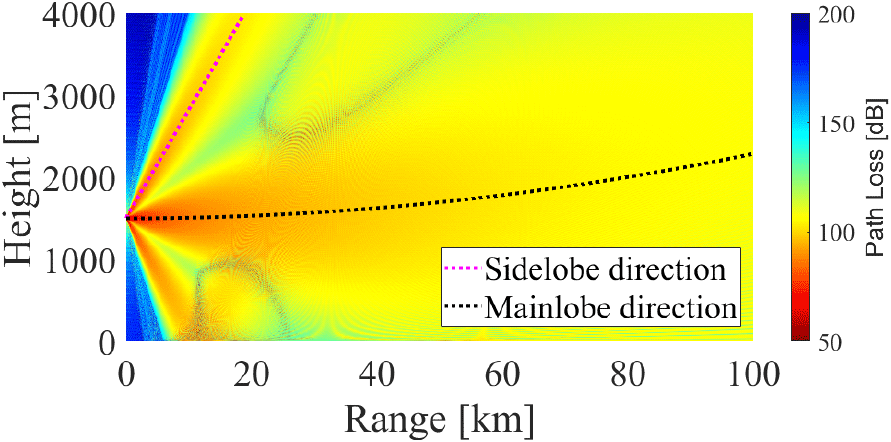
그림 1의 안테나 패턴을 식 (2)에 대입하고 이를 역 푸리에 변환하여 초기 필드 값을 구할 수 있다. 제안된 방법을 검증하기 위해서, 그림 1의 안테나 복사 패턴을 고려하여 표 1과 같은 조건에서 SSPE 기법을 이용해 자유 공간상에서 필드값을 계산하고, 이를 식 (3)~식 (5)에 대입하여 거리-고도별 경로 손실값을 계산하였다. 그 후, 주엽 및 측엽 지향 방향에 대한 경로 손실 값과 자유 공간 손실 값을 비교하였다. 그림 2는 거리-고도별 경로 손실 값으로 검은색 선은 지구 곡률을 고려한 주엽의 지향 방향이고 분홍색 선은 측엽 중 고도각 7.5°인 측엽의 지향 방향이다. 표 1은 SSPE 기법의 입력 파라미터로 주파수, 최대 거리 및 고도, 안테나 고도 및 고도각 값이다.
| Variables | Value |
|---|---|
| Frequency f | 300 MHz |
| Maximum range | 100 km |
| Maximum height | 4,000 m |
| Antenna height | 1,500 m |
| Antenna elevation angle | 0° |
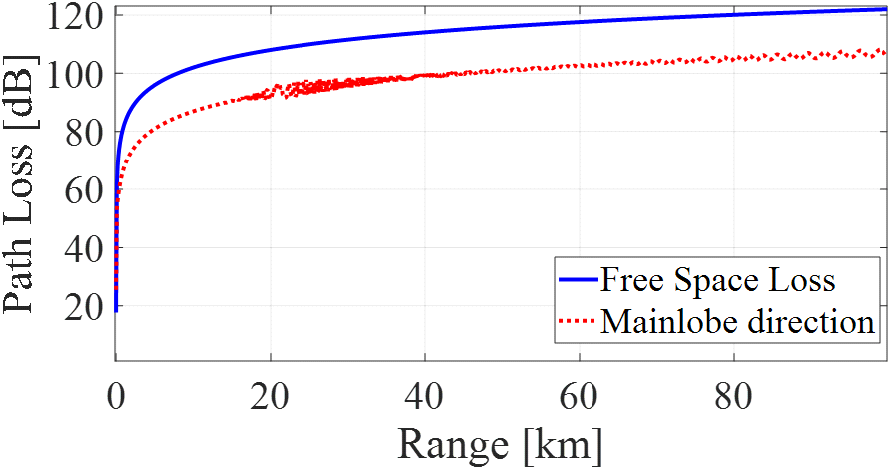
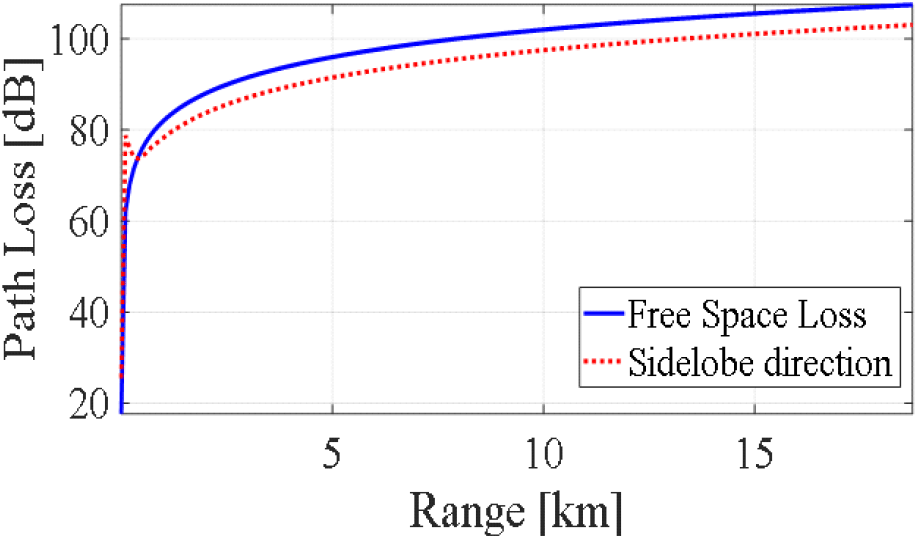
그림 3 및 그림 4는 각각 지구 곡률을 고려한 주엽, 측엽의 지향 방향으로의 경로 손실과 자유 공간 손실 값을 비교한 결과이다. 주엽의 경우 자유공간 경로 손실과 약 15 dB 정도의 차이를 보이고, 측엽의 경우 약 4.55 dB 정도의 차이를 보여 안테나 이득이 정확하게 고려되었음을 알 수 있다.
제안된 안테나 복사 패턴을 고려하는 방법을 통해 그림 1의 안테나와 같은 단일 가우시안 빔 이외의 복사 패턴을 포물형 방정식 기법 기반 전자파 전파 해석 방식에 적용할 수 있다. 포물형 방정식 기법 기반 방식은 대기 굴절률과 지구 곡률을 수정 굴절률을 통해 반영한다. 장거리 환경에서 전자파는 대류권을 통해 전파되는데, 대기의 비균질함으로 인해 굴절 현상이 발생한다. 대기의 비균질함은 굴절률 n과 굴절 계수 N으로 표현되는데 다음과 같이 기압, 기온, 수증기압으로 계산된다[7].
P:기압(hpa), T:기온(°K), e:수증기압(hpa)
식 (7)과 같이 계산되는 굴절률에 지구 곡률을 고려하여 수정 굴절률 m과 수정 굴절 계수 M을 정의한다[7].
ae:지구반지름 6,378 km, x:고도(km)
식 (9)를 통해 계산되는 수정 굴절 계수 M의 고도에 따른 변화량 ▽M=dM/dx(M unit/km)에 따라 전자파의 굴절 형태를 구분한다[5]. ▽M>157일 때는 아굴절(sub- refraction) 로 전자파는 지구 곡률보다 작게 굴절되어 위로 향한다. 78<▽M>157일 때는 일반 굴절로, 지구 곡률와 같이 굴절된다. 0<▽M>78일 때는 초굴절(super-refraction)로, 지구 곡률보다 크게 굴절되어 전자파가 지면을 향한다. 마지막으로 수정 굴절 계수의 고도에 따른 변화량이 음수가 되는 ▽M≤0인 경우 덕트에 해당하여 전자파가 도파관에 갇힌 것처럼 덕트 층에 갇힌 채로 전파된다. 이러한 굴절 현상에 전자파 전파 특성이 달라지므로 정확한 장거리 레이다 탐지거리 분석 시 수정 굴절 계수의 고려가 필요하다.
제안된 안테나 복사 패턴 고려 방식과 수정 굴절 계수를 이용하여 그림 1의 안테나를 이용하는 레이다의 대기 굴절률 및 지구 곡률이 고려된 탐지거리를 분석하였다. 레이다 탐지거리는 레이다로부터 방사된 전자파가 특정 레이다 단면적을 가지는 표적에 반사되고 다시 돌아오는 수신 전력을 계산하여 분석할 수 있다. 레이다로 돌아오는 수신 전력은 다음과 같이 정의된다[8].
Pt : 송신전력 Gt : 송신안테나 이득
Gr : 수신안테나이득 σ : 표적 RCS
SSPE는 연산 결과로 전기장의 세기를 제안하고, 이를 통해 경로 손실을 계산한다. 앞서 제안한 방법을 통해 안테나 이득이 고려된 경로 손실을 구하였고, dB scale에서 송신 전력을 더하면 특정 거리에서의 송신 안테나로 부터의 dBm 단위 수신 전력을 구할 수 있다. 특정 거리에서 isotropic한 패턴을 지니는 안테나가 수신하는 전력은 linear scale에서 다음의 식 (11)과 같이 계산된다.
이를 dB scale로 나타내면 다음과 같은데,
SSPE로 계산된 경로 손실에 송신 안테나 이득이 포함되어 있으므로 다음과 같이 표현할 수 있다.
표적에 반사되어 다시 안테나로 수신되는 수신 전력 식 (11)은 식 (12)를 통해 다음과 같이 표현할 수 있는데,
수신 안테나 이득 Gr은 송신 및 수신 안테나가 동일하고, 전파가 같은 경로를 통해 도달하였다고 가정하여, Gr = Gt = G를 경로 손실 계산에 반영하였다. 따라서, 식 (9)를 dB scale로 나타내면 다음과 같이 표현된다.
식 (15)을 이용하여 그림 1의 안테나 복사 패턴을 소스로 레이다 수신 전력을 계산할 수 있다. 표 2는 레이다 탐지거리를 계산한 파라미터로 SSPE 입력 파라미터와 송신 전력, 표적의 레이다 단면적, 수정 굴절 계수 변화량을 나타낸 것이다. 표 2와 같은 조건에서 레이다 수신 전력을 계산하면 그림 5와 같다.
| Variables | Value |
|---|---|
| Frequency f | 300 MHz |
| Maximum range | 100 km |
| Maximum height | 4,000 m |
| Antenna height | 1,500 m |
| Antenna elevation angle | 0° |
| ∇ M | 157 |
| Transmit power | 70 dBm (10 kW) |
| Target RCS | 25 m2 |
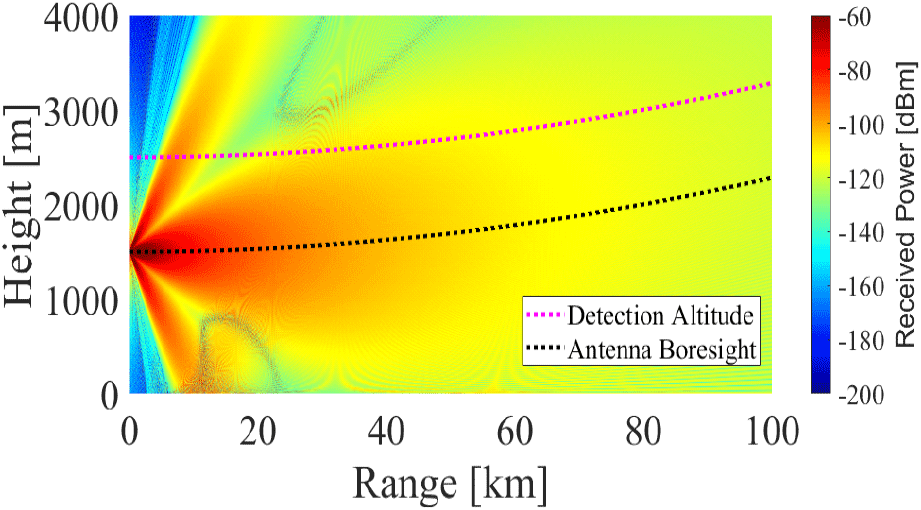
그림 5는 레이다 단면적이 25 m2인 표적에 반사되어 다시 같은 안테나로 동일한 경로를 따라 수신되는 수신 전력을 거리-고도별로 나타낸 것이다. 레이다가 표적을 탐지할 수 있는 최소 수신 전력 sensitivity를 −115 dBm이라고 가정하면, 레이다 최대 탐지거리는 수신 전력이 −115 dBm 보다 큰 거리가 된다. 이를 통해 그림 5의 검은 색 선 경로인 지구 곡률을 고려한 안테나 보어사이트 방향 고도 1,500 m에서의 수신 전력을 구할 수 있다.
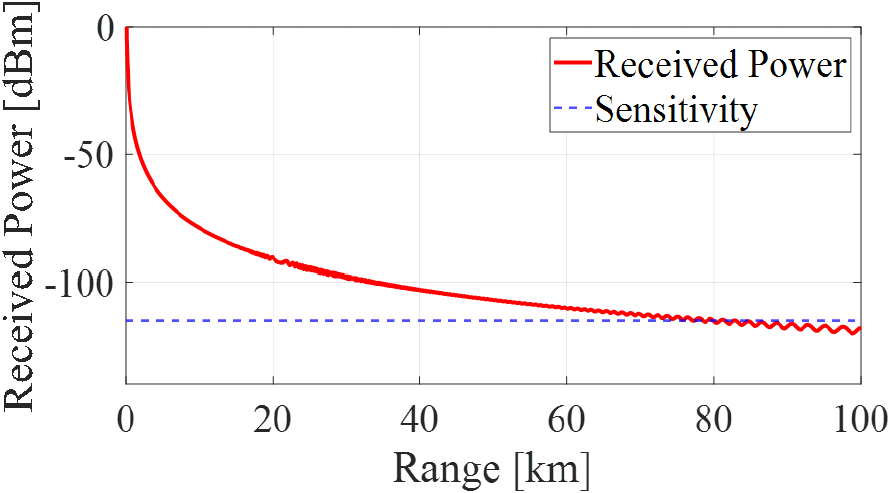
그림 6은 안테나 보어사이트 방향인 고도 1,500 m 높이에서의 수신 전력이다. 지면 반사로 인한 다중 경로 페이딩으로 인해 정확한 탐지거리는 알 수 없지만 약 78 km 전후 거리에서 수신 전력이 −115 dBm 이하로 떨어져 위와 같은 조건에서 보어사이트 방향으로 약 78 km의 탐지거리를 갖는 것을 알 수 있다.
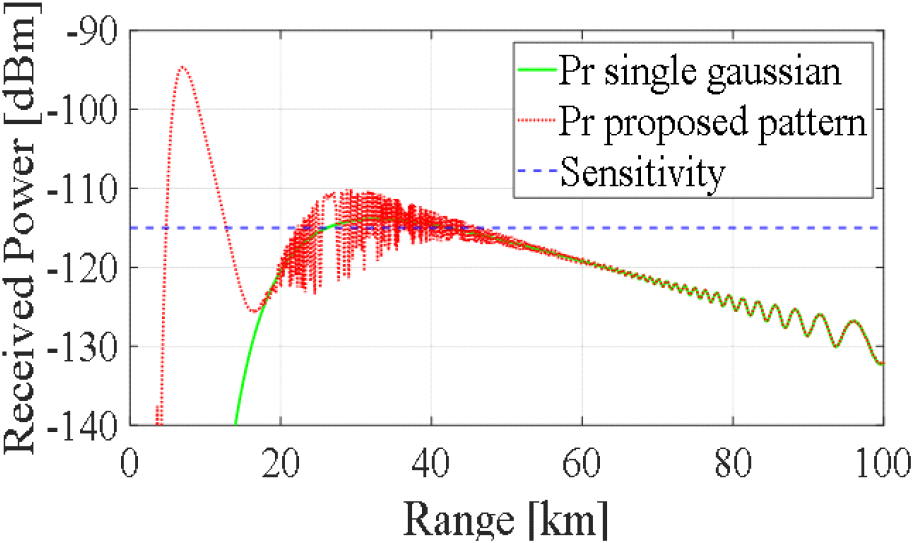
표적이 고도 2,500 m에 존재한다고 가정하여, 탐지 고도를 2,500 m로 설정하여 분석하면 그림 5에서 분홍색 선처럼 지구 곡률을 고려한 경로가 된다. 분홍색 선과 같은 경로의 경우, 안테나 보어사이트 방향보다 측엽에 의한 영향을 크게 받아, 기존 SSPE 기법에서 단일 가우시안 빔을 사용했던 것과는 상이한 결과를 보인다. 단일 가우시안 빔을 소스로 사용하였을 때 2,500 m에서의 수신 전력과 그림 1의 안테나 복사 패턴을 사용하였을 때의 수신 전력인 그림 5의 분홍색 선에 따른 수신 전력을 분석하면 그림 7과 같다.
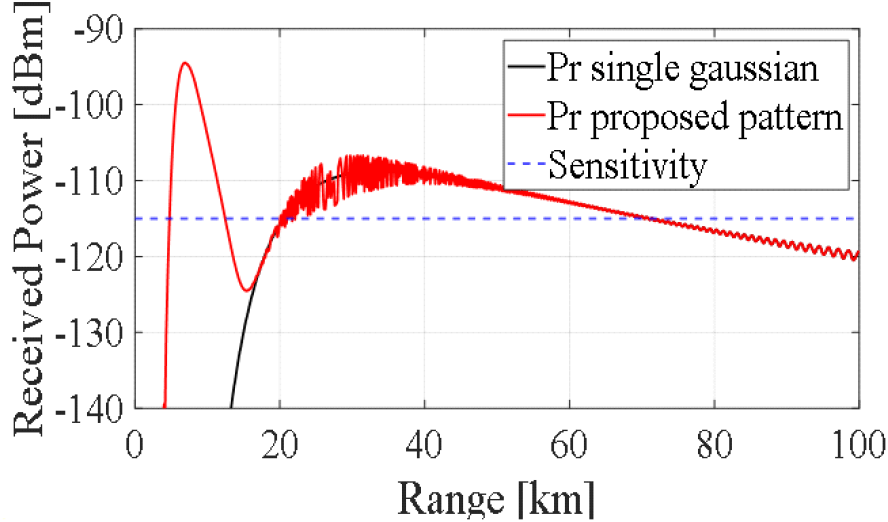
그림 7은 탐지 고도 2,500 m에서의 단일 가우시안 빔을 사용하였을 때와 그림 1의 안테나 복사 패턴을 사용하였을 때의 수신 전력을 나타낸 것이다. Pr single Gaussian으로 표기된 검은 색 선이 단일 가우시안 빔 소스, Pr proposed pattern으로 표기된 붉은 색 선이 그림 1의 복사 패턴을 소스로 사용하였을 시 수신 전력 결과이다. 5 km 이내 범위에서는 포물형 방정식 기법 기반 전자파 해석 방법의 특성상 일정 각도 이상의 범위에서는 해석 결과가 정확하지 않아 유의미한 결과로 볼 수 없다. 5~12 km 부근에서 측엽에 영향을 받는 그림 1의 복사 패턴을 소스로 사용한 경우 높은 수신 전력 값을 보여 레이다 탐지거리로 분석되는데, 단일 가우시안 빔을 소스로 사용하였을 때는 탐지가 불가능한 영역이므로 본 영역은 측엽에 의한 탐지거리로 분석된다. 약 15 km 이상의 영역에서는 주엽에 의한 영향이 우세하여 단일 빔을 사용하였을 때와 그림 1의 복사 패턴을 사용하였을 때의 탐지거리 차이가 미비하다. 그림 1의 복사 패턴을 소스로 사용하였을 때 탐지거리는 측엽에 의한 영향인 약 5~12 km구간과 20~70 km까지의 영역으로 보어사이트 방향에 비해 감소한 결과를 보였다.
수정 굴절 계수 변화량이 지표면에서부터 음수 값을 가지는 경우, 대기에 표면 덕트 현상이 발생하여 덕트 층 내에서 전파가 갇힌 듯이 진행하는 현상이 발생한다. 표 2와 같은 조건에서 수정 굴절 계수 변화량이 157인 자유 공간과 −300인 표면 덕트 현상 발생 시, 그림 1의 안테나 복사 패턴을 소스로 보어사이트 방향과 탐지 고도 2,500 m에서의 수신 전력을 비교하면 그림 8과 같다.
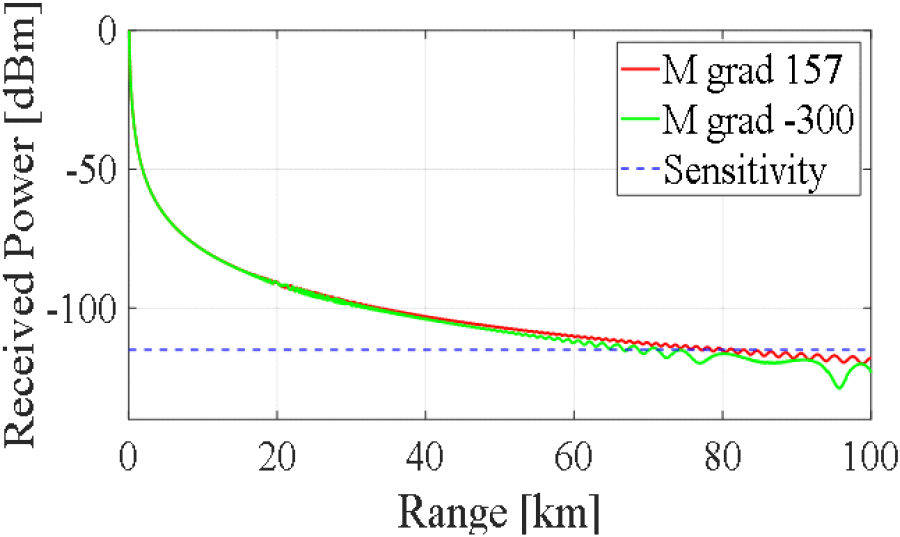
그림 8은 자유 공간과 덕트 현상 발생 시의 안테나 보어사이트 방향인 고도 1,500 m 높이에서의 수신 전력을 비교한 것이다. M grad 157로 표기된 붉은색 선은 수정 굴절 계수 변화량이 157일 때, M grad −300으로 표기된 초록색 선은 수정 굴절 계수 변화량이 −300일 때 거리에 따른 레이다 수신 전력이며, 최소 수신 전력 sensitivity−115 dBm은 푸른색 점선으로 표기하였다.
표면 덕트의 영향으로 전파가 덕트에 갇혀 탐지거리가 null 부분을 제외하면 약 66 km로 자유 공간 대비 탐지거리가 10 km 정도 감소하였다. 그림 9는 탐지 고도 2,500 km에서 수신 전력을 비교한 것으로 덕트 현상 발생 시 자유 공간 대비 수신 전력이 낮아져, 측엽에 의한 탐지거리 영역인 5~12 km 영역을 제외하고는 대부분의 영역에서 sensitivity보다 낮은 수신 전력을 갖는다. 20~40 km 영역에서 일부 탐지거리로 판단되는 영역이 존재하지만, 다중 경로 페이딩 현상에 의한 것으로 탐지거리로 판단하기는 어렵다. 그러므로 표면 덕트 현상 발생 시 고도 2,500 m에 존재하는 표적 탐지는 측엽에 의한 높은 수신 전력을 보이는 5~12 km 부근의 영역에서만 가능할 것이라고 분석된다. 동일한 표면 덕트 조건에서 단일 가우시안 빔과 그림 1의 복사 패턴을 소스로 사용하였을 때 탐지거리 차이는 그림 10과 같다.
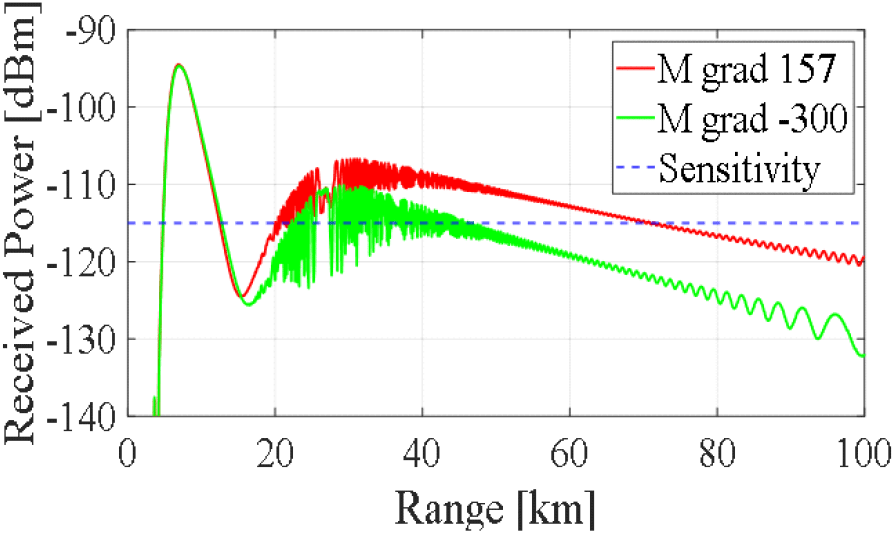
그림 10은 표면 덕트 현상이 발생하는 수정 굴절 계수 변화량이 −300일 때 단일 가우시안 빔과 그림 1의 복사 패턴을 소스로 사용하였을 때 레이다 탐지거리이다. 측엽이 존재하는 그림 1의 복사 패턴 소스와는 다르게 단일 가우시안 빔을 사용하였을 때는 일부 구간에서만 senesitivity보다 높은 수신 전력 값을 가져 대부분의 영역에서 탐지가 불가능하다고 분석된다. 측엽이 존재하는 그림 1의 복사 패턴을 소스로 사용한 경우, 측엽에 의해 5~12 km인 근거리 영역이 탐지거리로 분석되어 차이를 보인다.
이를 통해 기존 SSPE 기법에서 사용하였던 단일 가우시안 빔을 소스로 이용하였을 때 고려하지 못하였던 측엽에 의한 영향을 주엽, 측엽 및 이득이 존재하는 안테나 복사 패턴을 SSPE 기법에 대입하여 안테나 복사 패턴을 정확히 고려하였다. 제안된 방식을 통해 대기 굴절률에 따른 굴절 현상, 지구 곡률, 안테나 복사 패턴이 모두 고려된 레이다 탐지거리를 분석하였다.
Ⅲ. 결 론
본 논문에서는 경계조건을 PEC로 해석하는 SSFT 기반의 포물형 방정식 기법을 이용해 안테나 복사 패턴을 고려한 레이다 탐지거리 분석 방법을 제안하였다. 주엽과 측엽을 가지며, 15 dBi 이득을 가지는 안테나 패턴에 대한 주엽 및 측엽 지향 방향의 경로 손실과 자유 공간 손실의 비교를 통해 실제 안테나 패턴을 고려되었음을 확인하였다. 안테나 복사 패턴을 고려한 포물형 방정식 기법을 활용하여 25 m2의 레이다 단면적을 가진 표적에 대해 대기 굴절률에 따른 자유 공간과 덕트 현상 발생 시의 수신 전력을 계산하여 −115 dBm의 sensitivity와 10 kW의 송신 전력을 가지는 레이다의 탐지거리를 단일 가우시안 빔과 측엽이 존재하는 패턴을 소스로 사용하였을 때를 예시로 분석하였다.
본 논문에서 제안된 방법은 실제 레이다 안테나 패턴을 포물형 방정식 기법 기반 방식에 적용할 수 있어 대기 굴절률과 지구 곡률을 고려할 수 있으므로 실제 레이다 운용 환경을 반영한 정확한 탐지거리 분석이 가능할 것으로 기대된다.