The Journal of Korean Institute of Electromagnetic Engineering and Science

The Korean Institute of Electromagnetic Engineering and Science

J. Korean Inst. Electromagn. Eng. Sci. 2024; 35(12):997-1004

pISSN: 1226-3133, eISSN: 2288-226X

DOI: https://doi.org/10.5515/KJKIEES.2024.35.12.997

논문/REGULAR PAPER

소재의 평면파 차폐효과에 대한 이론적 및 실험적 분해법 비교

박현호^†

Comparison of Theoretical and Experimental Decompositions for Plane Wave Shielding Effectiveness of Materials

Hyun Ho Park^†

수원대학교 전기전자공학부

School of Electric & Electronic Engineering, The University of Suwon

^†Corresponding Author: Hyun Ho Park (e-mail: hhpark@suwon.ac.kr)

© Copyright 2024 The Korean Institute of Electromagnetic Engineering and Science. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Jul 12, 2024; Revised: Jul 22, 2024; Accepted: Aug 02, 2024

Published Online: Dec 31, 2024

요 약

본 논문에서는 소재의 평면파 차폐효과에 대한 Schelkunoff의 이론적인 분해법인 반사손실, 흡수손실, 다중반사손실과 전력균형원리를 토대로 한 실험적인 분해법에서의 반사손실과 흡수손실의 관계를 규명하였다. 이론적인 분해법에서의 반사손실과 흡수손실은 실험적인 분해법에서의 그것과 다름을 수학적으로 확인하였고, 상호간의 관계를 엄밀하게 유도하였다. 도전성 차폐 소재와 유전 흡수 소재에 대해서 주어진 물성을 이용하여 이론적인 차폐효과를 계산하고 반사와 흡수에 의한 차폐효과 기여도를 비교하였다. 또한 3차원 수치해석을 통해 실험적인 분해법에서 반사와 흡수의 차폐효과 기여도를 계산하였고 해석적으로 유도한 값들과 비교하여 정확성을 확인하였다.

Abstract

This study investigated the relationship between reflection, absorption, and multiple reflection losses in Schelkunoff's theoretical decomposition method for the plane-wave shielding effectiveness (SE) of materials and reflection and absorption losses in an experimental decomposition method based on the power balance principle. It was mathematically confirmed that the reflection and absorption losses in the theoretical decomposition method differed from those in the experimental decomposition method, and that their mutual relationships were strictly derived. The theoretical SE was calculated using the physical properties of the conductive shielding and dielectric absorption materials, and the contributions of reflection and absorption were compared. In addition, through a 3D numerical analysis, the contribution of the shielding effect of reflection and absorption was calculated using the experimental decomposition method, and its accuracy was confirmed by comparing it with the results of analytically derived equations.

Keywords: Shielding Effectiveness; Reflection Loss; Absorption Loss; Theoretical Decomposition; Experimental Decomposition

Ⅰ. 서 론

전자파 차폐 기술은 전자기기 내부에서 발생하는 원치 않는 전자파의 방사를 줄여 다른 기기로의 간섭을 저감시키거나 외부 전자파로부터 전자기기를 보호(방호)하기 위해서 반드시 필요한 기술이다. 전자파를 효과적으로 차폐하기 위해서는 전자파 소스의 종류와 위치, 주파수 대역에 따른 차폐 소재의 선정과 차폐 구조의 설계가 중요하다. 소재나 구조의 전자파 차폐 성능은 일반적으로 차폐효과(SE, shielding effectiveness)로 평가한다. 소재의 평면파 차폐효과는 공기와 소재의 임피던스 차이에 의해 발생하는 반사손실과 전자파가 소재 내에서 열에너지로 전환되는 흡수손실에 의해 주로 결정된다^[1],[2]. 만약 소재의 두께가 표피두께보다 얇으면 소재 내에서 발생하는 다중반사손실을 더해 준다. 이러한 차폐효과 분해법은 1943년 Schelkunoff에 의해서 이론적으로 정립되었다^[1]. 하지만 실제 차폐나 흡수소재의 반사나 흡수에 의한 차폐 기여도를 2 포트 산란계수 측정을 통해 실험적으로 정의할 때 사용되는 반사와 흡수손실은 이론적인 분해법의 정의와 다르다. 그럼에도 불구하고 소재를 연구하는 많은 연구자들이 이들을 아직 혼용하는 경우가 많다^[3]~[5].

본 논문에서는 소재의 평면파 차폐효과에 대한 이론적 및 실험적 정의에서의 반사손실과 흡수손실을 수학적으로 비교하여 이들이 명확히 다름을 보여줄 것이다. 그리고 이들의 관계가 특정 조건에서 해석적으로 어떻게 되는지도 유도할 것이다. 전도성 차폐 소재와 유전 흡수 소재들에서 반사와 흡수에 의한 차폐효과 기여도를 분석하고 이들 관계를 살펴볼 것이다. 또한 실험적 정의에서의 반사와 흡수손실을 측정 대신 3차원 수치해석을 통해 얻는 2 포트 산란계수를 이용하여 계산하였으며, 이론식을 통해 계산한 결과와 비교하여 그 정확성을 검증하였다.

Ⅱ. 차폐효과의 이론적인 분해법^[1],[6],[7]

그림 1에서는 유한한 두께를 가지는 평판형 소재의 평면파 차폐 메커니즘을 보여준다. 공기 중의 전자파가 소재를 만나게 되면 전자파의 파동 임피던스와 소재의 임피던스 차이에 의해서 공기와 소재의 경계면에서 반사가 일어난다. 일부 전자파는 소재 내로 들어가 소재의 손실 특성에 의해서 그 크기가 지수 함수적으로 감소한다. 감소된 전자파는 소재와 공기의 경계면에서 다시 반사가 일어나고 일부는 투과하게 된다. 따라서 소재의 차폐효과는 입사한 전자파와 투과한 전자파의 비로 나타내어진다.

그림 1. | Fig. 1. 소재의 평면파 차폐 메커니즘 | Plane wave shielding mechanism of materials.

Download Original Figure

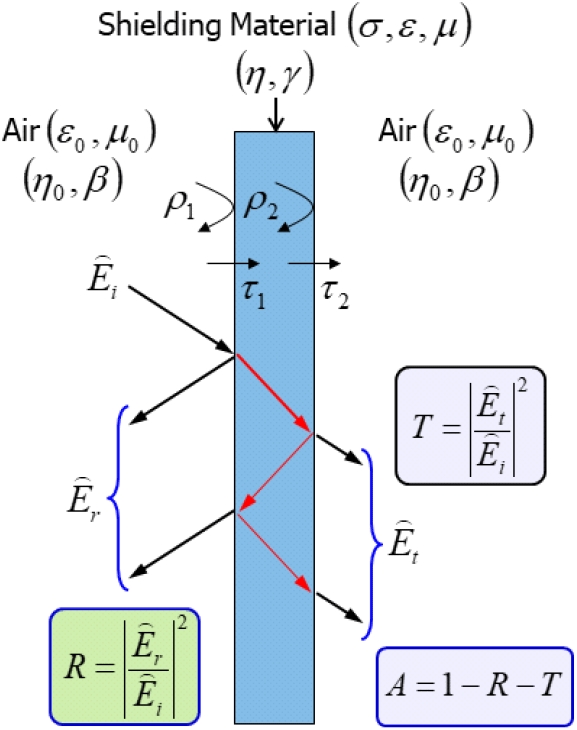
공기와 소재의 전파상수와 고유 임피던스를 각각 β, η₀와 γ, η라 하고, 공기와 소재가 이루는 두 경계면에서의 반사계수와 투과계수를 각각 ρ₁, τ₁과 ρ₂, τ₂로 나타내고, 공기와 소재의 경계면에서 전기장과 자기장의 접선 성분이 연속이라는 경계조건을 적용하면 입사파 $E^i$ 와 투과파 $E^t$ 의 비(1/S₂₁)를 식 (1)과 같이 나타낼 수 있다.

E^i E^t = η + η 0 2 4 η η 0 e γ t 1 − η − η 0 η + η 0 2 e − 2 γ t,

(1)

여기서 ρ₁=(η-η₀)/(η+η₀), τ₁=2η/(η+η₀)=1+ρ₁, ρ₁=−ρ₂, τ₂=1+ρ₂=1−ρ₁이며, t는 소재의 두께를 나타낸다. 식 (1)을 반사계수 ρ₁으로 나타내면 식 (2)와 같다.

E^i E^t = 1 1 − ρ 12 e γ t 1 − ρ 12 e − 2 γ t = 1 τ 1 τ 2 e γ t 1 − ρ 12 e − 2 γ t .

(2)

결과적으로 차폐효과는 입사파와 투과파의 크기 비를 dB 값으로 나타내어 식 (3)과 같이 정의된다.

S E = 20 log 10 E^i E^t = S E R S + S E A S + S E M S,

(3)

여기서 $S E R S$ 는 반사손실, $S E A S$ 는 흡수손실, 그리고 $S E M S$ 는 다중반사손실이라 하고, Schelkunoff는 식 (4)~식 (6)과 같이 정의하였다.

S E R S = 20 log 10 1 1 − ρ 12 = 20 log 10 1 τ 1 τ 2,

(4)

S E A S = 20 log 10 e γ t,

(5)

S E M S = 20 log 10 1 − ρ 12 e − 2 γ t .

(6)

식 (4)~식 (6)를 이용하면 차폐효과에서 반사손실, 흡수손실, 그리고 다중반사손실의 기여도를 계산할 수 있다. 이들은 소재의 유전율, 투자율, 전도율과 같은 물성이 주어지면 얻을 수 있다. 하지만 실험적으로 SE을 얻었다고 해서 식 (4)~식 (6) 값으로 분해할 수는 없다. 그리고 도전성 소재에서 만약 소재의 두께가 표피두께보다 1.75 배 이상 크면 식 (5)의 흡수손실은 15 dB 이상이 되어 식 (6)의 다중반사손실은 무시할 수 있다. 결론적으로 식 (3)처럼 차폐효과를 세 가지 손실 항으로 분해하는 것을 Schelkunoff의 분해법이라 하고 본 논문에서는 차폐효과의 ‘이론적인 분해법’이라 부르겠다.

Ⅲ. 차폐효과의 실험적인 분해법^[2],[8],[9]

이번에는 측정을 통해 얻은 소재의 차폐효과 값에서 반사손실과 흡수손실을 분해하는 방법을 살펴보자^[2],[8],[9]. 통상 소재의 원역장(평면파) 차폐효과를 측정할 때, ASTM D4935 방법을 많이 사용한다^[10]. 이 방법은 50 Ω으로 설계된 동축선로를 측정 지그로 사용하기 때문에 이 지그는 측정 계측기의 내부 임피던스 50 Ω과 정합되어 있다고 볼 수 있다. 따라서 다음과 같이 그림 1의 구조에서 입사파에 대한 반사파의 비를 S₁₁, 입사파와 투과파의 비를 S₂₁으로 나타낼 수 있다^[2].

S 11 = E^γ E^i = ρ 1 1 − e − 2 γ t 1 − ρ 12 e − 2 γ t,

(7)

S 21 = E^t E^i = 1 − ρ 12 e − γ t 1 − ρ 12 e − 2 γ t .

(8)

한편 입사전력과 반사전력의 비율을 반사율(R)로 정의하고 입사전력과 투과전력의 비율을 투과율(T)로 정의하면 이들을 식 (7) 및 식 (8)에서 나타낸 산란계수 크기의 제곱으로 나타낼 수 있다.

R = S 11 2 = E^γ E^i 2 = ρ 1 1 − e − 2 γ t 1 − ρ 12 e − 2 γ t 2,

(9)

T = S 21 2 = E^t E^i 2 = 1 − ρ 12 e − γ t 1 − ρ 12 e − 2 γ t 2 .

(10)

전력균형원리(power balance principle)에 의해 결과적으로 흡수율(A)은 식 (11)과 같이 정의된다.

A = 1 − R − T = 1 − S 11 2 − S 21 2 = 1 − ρ 1 1 − e − 2 γ t 1 − ρ 12 e − 2 γ t 2 − 1 − ρ 12 e − γ t 1 − ρ 12 e − 2 γ t 2 .

(11)

차폐효과는 S₂₁또는 T를 이용하여 다음과 같이 정의할 수 있고, 반사에 의한 성분과 흡수에 의한 성분의 합으로 식 (12)과 같이 표현할 수 있다.

S E = 20 log 10 1 S 21 ≡ 10 log 10 1 T = S E R P + S E A P .

(12)

반사에 의한 차폐효과 성분과 흡수에 의한 차폐효과성분은 식 (13) 및 식 (14)와 같이 정의된다.

S E R P = 10 log 10 1 1 − R = 10 log 10 1 1 − S 11 2,

(13)

S E A P = 10 log 10 1 − R T = 10 log 10 1 − S 11 2 S 21 2 .

(14)

소재의 평면파 차폐효과 측정은 2 포트 산란계수 측정을 통해 이루어지며, S₂₁과 S₁₁이 얻어지면 소재의 차폐효과 중 반사에 의한 영향과 손실에 의한 영향을 식 (13)및 식 (14)을 통해 계산할 수 있다. 이와 같이 차폐효과를분해하는 것을 Schelkunoff의 분해법과 구분하기 위해서참고문헌 [8]에서는 부정합(mismatch) 분해법이라고 하였다. 본 논문에서는 이를 차폐효과의 전력균형(power balance)분해법 또는 ‘실험적인 분해법’이라고 부를 것이다.

Ⅳ. 두 분해법의 해석적인 관계

식 (3)의 이론적인 분해법을 이용하든 식 (12)의 실험적인 분해법을 이용하든 차폐효과(SE)는 동일하다. 하지만두 분해법에서의 반사손실과 흡수손실의 의미는 분명 다르다. 이는 수학적으로 식 (4) 및 식 (5)와 식 (13) 및 식 (14)를 비교해 보아도 명확히 알 수 있다. 그러나 차폐 소재나 흡수 소재를 다루고 있는 논문들에서 이들을 혼용해서 사용하는 경우가 많다[3]~[5]. 이들 문헌에서는 식 (3) 에서 $S E M S ≈ 0$ 일 때 $S E R S = S E R P, S E A S = S E A P$ 로 나타내고 있다. 하지만 식 (4) 및 식 (5) 그리고 식 (13) 및 식 (14) 에서 보듯이 이들은 분명히 수학적으로 서로 다르다. 본절에서는 특정 조건에서 이들의 관계를 살펴 볼 것이다.

식 (13)으로부터 식 (15)와 같은 관계를 얻을 수 있다.

S E R P = 10 log 10 1 1 − S 11 2 ≈ 10 log 10 1 1 − S 112 .

(15)

식 (15)가 성립하기 위해서는 $1 − S 112 ≈ 1 − S 11 2$ 이어야 하는데, 이 근사가 성립하는 조건을 찾기 위해서 S₁₁=|S₁₁|e^jθ로 놓고 식을 전개하면 식 (16) 및 식 (17)과 같은 관계를 얻을 수 있다.

S 112 = S 11 2 e j 2 θ = S 11 2 cos 2 θ + | j | S 11 2 sin 2 θ

(16)

1 − S 112 = 1 − S 11 2 cos 2 θ 2 + S 11 4 (sin 2 θ) 2 = 1 − 2 S 11 2 cos 2 θ + S 11 4

(17)

만약 위 식에서 cos2θ ≃ 1이면,

1 − 2 S 11 2 + S 11 4 = 1 − S 11 2 2 = 1 − S 11 2

(18)

이 된다. 따라서 cos2θ ≃ 1이면 $1 − S 112 ≈ 1 − S 11 2$ 이 성립하게 된다. 즉 S₁₁의 위상각(θ)이 거의 0이면 위의 근사가 유효함을 알 수 있다. 이를 이용하면 $S E R P$ 과 $S E A P$ 을 식 (19)와 같이 전개할 수 있다.

S E R P ≈ 10 log 10 1 1 − S 112 = 10 log 10 1 − ρ 12 e − 2 γ t 2 1 − ρ 12 1 − ρ 12 e − 4 γ t = 10 log 10 1 1 − ρ 12 + 20 log 10 1 − ρ 12 e − 2 γ t − 10 log 10 1 − ρ 12 e − 4 γ t

(19)

S E A P = 10 log 10 1 − S 11 2 S 21 2 ≈ 10 log 10 1 − S 112 S 212 = 10 log 10 1 − S 112 S 212 = 10 log 10 1 − ρ 12 e − 4 γ t 1 − ρ 12 e − 2 γ t = 20 log 10 e γ t + 10 log 10 1 1 − ρ 12 + 10 log 10 1 − ρ 12 e − 4 γ t

(20)

결과적으로 측정을 통해 얻은 $S E R P$ 과 $S E A P$ 는 Schelkunoff 가 정의한 $S E R S$ 과 $S E A S$ 를 이용하여 다음과 같이 나타낼 수 있다.

S E R P ≈ 12 S E R S + S E M S − 10 log 10 1 − ρ 12 e − 4 γ t,

(21)

S E A P ≈ S E A S + 12 S E R S + 10 log 10 1 − ρ 12 e − 4 γ t .

(22)

또한 식 (21) 및 식 (22)를 이용하면 $S E R P$ 과 $S E A P$ 는 항상 다음과 같은 대소 관계를 만족함을 알 수 있다.

S E A P − S E R P = S E A S − S E M S + 20 log 10 1 − ρ 12 e − 4 γ t,

(23)

S E A S = 20 log 10 e γ t > 0, S E M S = 20 log 10 1 − ρ 12 e − 2 γ t < 0 − S E M S + 20 log 10 1 − ρ 12 e − 4 γ t > 0

(24)

S E A P − S E R P > 0 → S E A P > S E R P .

(25)

이는 S₁₁의 위상각(θ)이 거의 0(cos2θ=1)인 소재의 경우 실험적 분해법에서의 흡수에 의한 손실이 항상 반사에 의한 손실보다 큼을 의미한다.

Ⅴ. 계산 결과 및 수치해석 검증

앞 절들에서 유도한 이론적인 수식을 이용하여 두 종의 도전성 차폐 소재와 두 종의 유전 흡수 소재에 대해서 차폐효과 및 반사손실과 흡수손실을 계산하였다. 이론적인 분해법에서는 주어진 소재의 물성을 이용하여 전파상수와 고유 임피던스를 계산한 다음 식 (3)~식 (6)에 대입하여 이들을 계산하였다. 실험적인 분해법에서는 우선 식 (12)~식 (14)에 식 (9) 및 식 (10)을 대입하여 이론적으로 계산하였고, 또한 측정을 대신하여 3차원 수치해석 시뮬레이션을 실시하여 산란계수를 얻고 이를 통해 식 (13) 및 식 (14)에 대입하여 차폐효과 중 반사손실과 흡수손실을 계산하였다. 시뮬레이션은 CST MWS(microwave studio)^[11] 를 이용하였고, 그림 2와 같이 100×100 mm² 크기의 평판형 소재에 평면파가 입사하는 간단한 구조를 사용하였다. 평면파가 왜곡 없이 입사 및 투과되도록 하기 위해서 전기장이 수직인 면에는 전기장 경계조건을, 자기장이 수직인 면에는 자기장 경계조건을 적용하였다.

그림 2. | Fig. 2. 차폐 해석을 위한 3차원 시뮬레이션 구조 | 3-D simulation geometry for shielding analysis.

Download Original Figure

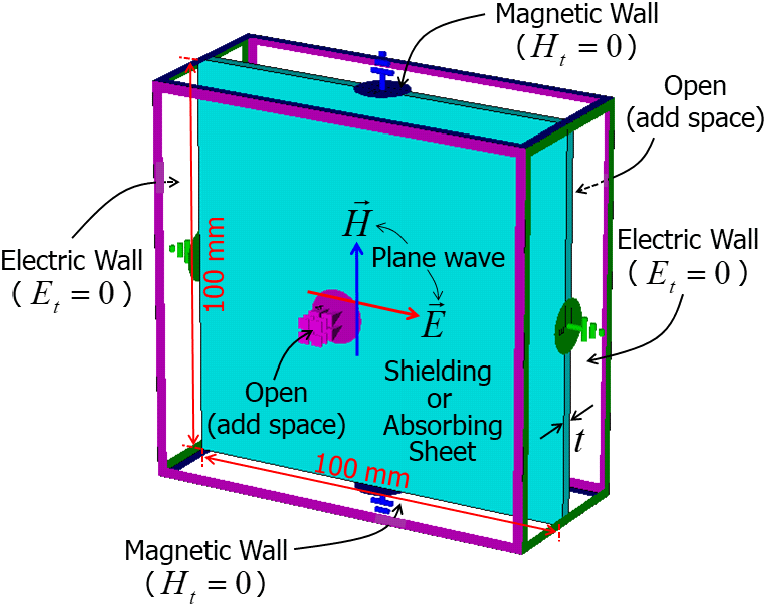
그림 3에서는 두 종의 도전성 차폐 소재의 차폐효과와 두 분해법에서의 반사와 흡수손실을 비교하였다. σ=10⁴ S/m인 도전성 차폐 소재는 0.1 mm의 두께를 가지고 σ=10 S/m인 도전성 소재는 3 mm의 두께를 가진다. 두 분해법에서의 전체 차폐효과는 정확히 일치하지만 차폐효과를 구성하고 있는 반사손실과 흡수손실은 서로 다름을 알 수 있다. 이론적인 분해법에서는 저주파수에서 반사손실이 매우 크고 주파수가 증가하면서 급격히 감소하는 반면 흡수손실은 거의 0 dB에서 시작해서 빠르게 증가한다. 또한 전도율이 σ=10⁴ S/m일 때는 6 GHz까지 반사손실이 흡수손실보다 큰 반면, σ=10 S/m일 때는 2.3 GHz까지 반사손실이 흡수손실보다 크고 그 이상의 주파수에서는 흡수손실이 반사손실보다 크다. 실험적인 분해법에서는 전주파수 대역에서 흡수손실이 반사손실보다 더 크며, 주파수가 증가함에 따라 반사손실은 서서히 감소하는데 흡수손실은 서서히 증가한다. 이는 전도율에 상관없이 동일한 경향을 보인다. 결과적으로 이러한 차이는 이론적인 분해법에서의 반사손실 $S E R S$ 과 흡수손실 $S E A S$ 의 의미가 실험적인 분해법에서의 반사손실 $S E R P$ 과 흡수손실 $S E A P$ 의 의미와 서로 다르기 때문에 발생한다.

그림 3. | Fig. 3. 두 도전성 소재의 차폐효과와 그들의 성분 비교 | Comparison of shielding effectiveness and their components of two conductive materials.

Download Original Figure

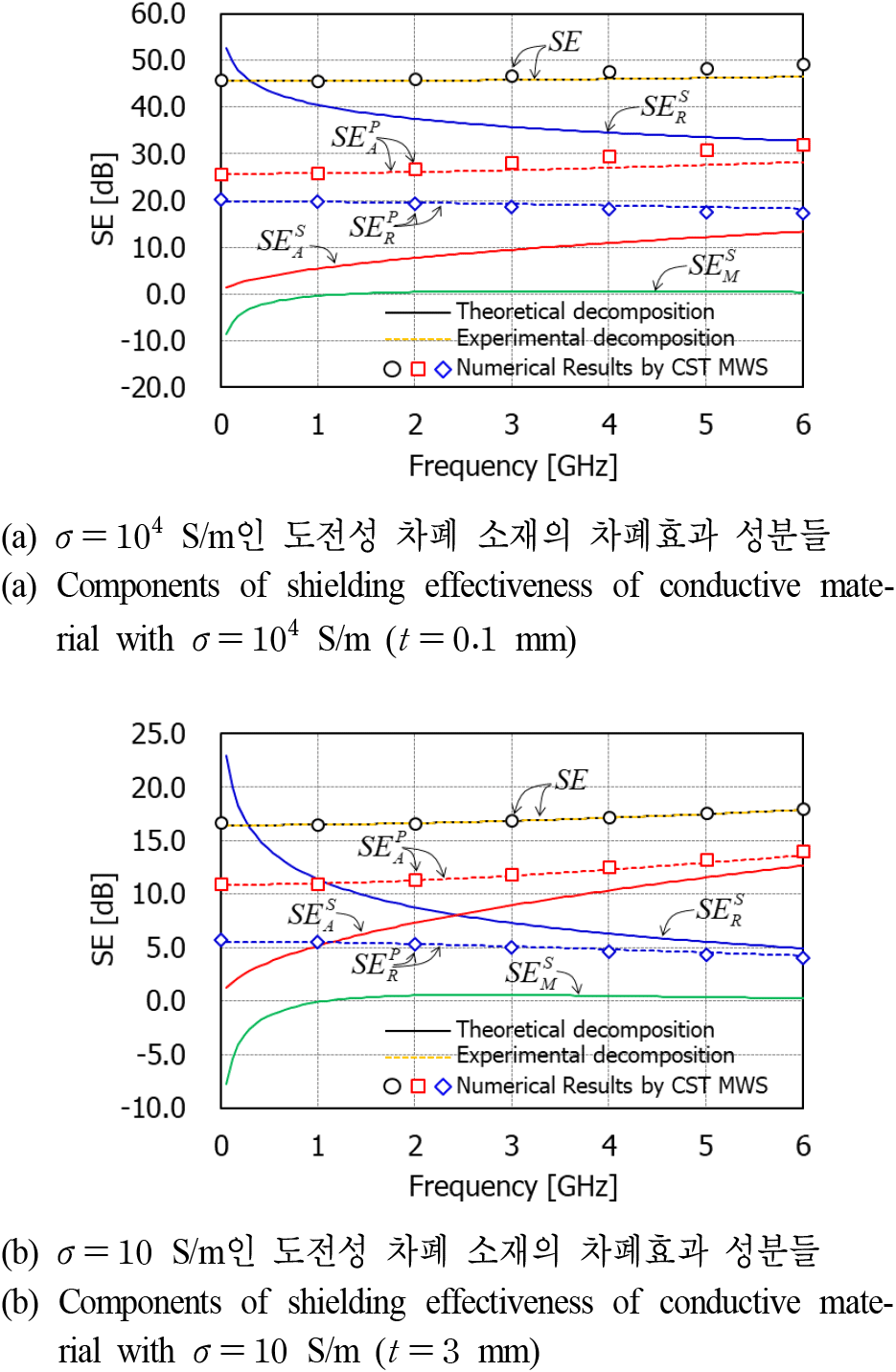
이론적인 분해법에서 다중반사손실 $S E M S$ 은 1 GHz 이하의 주파수 대역에서 (−) 값을 가져 차폐효과를 낮추는 효과를 준다. 반면 1 GHz 이상에서는 거의 0 dB에 가까운 (+) 값을 가진다. 결과적으로 주파수가 증가하면 표피두께가 감소하게 되어 소재 내부의 흡수손실 $S E A S$ 이 증가하게 되고 이로 인해 다중반사손실은 무시할 수 있음을 알 수 있다. 다중반사손실이 (−) 값을 가진다는 것은 소재 내에서 소재와 공기의 두 경계면에서 다중 반사되다가 결국 투과된다는 의미이고, 반대로 (+) 값을 가진다는 것은 입사면 쪽으로 다시 반사된다는 의미이다.

또한 그림 3에서 실험적인 분해법에서의 차폐효과와 반사 및 흡수손실은 3차원 수치해석을 통해 얻은 산란계수를 이용하여 계산한 결과(○, □, ◊)와도 비교하였으며, 해석적으로 계산한 결과와 상당히 잘 일치함을 알 수 있다.

다음은 유전 흡수 소재에 대해 차폐효과와 두 분해법에서의 각 손실을 비교하였다. 분석에 사용된 두 유전 흡수 소재는 Laird사의 Eccosorb LS26과 LS22 모델이다^[12]. 이 두 유전 소재의 물성인 주파수에 따른 복소 비유전율은 CST MWS에서 제공하며 그림 4에 나타내었다.

그림 4. | Fig. 4. 유전 흡수 소재들의 복소 비유전율 | Complex relative permittivity of dielectric absorbing materials.

Download Original Figure

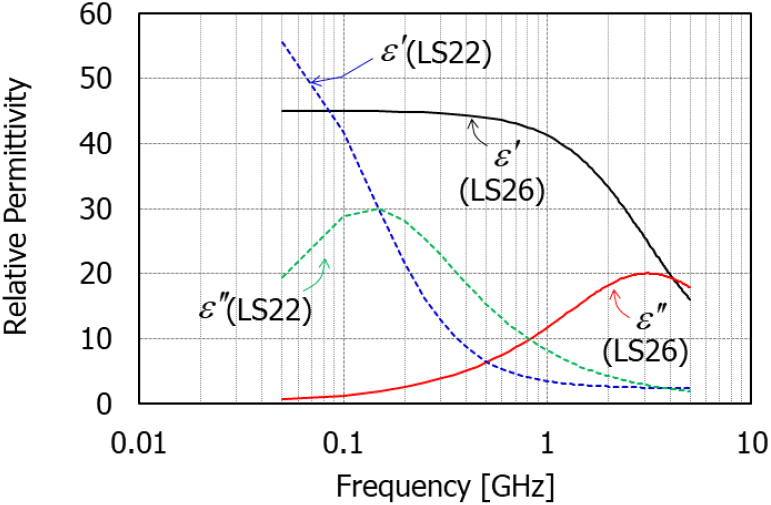
LS26 모델은 1 GHz까지 40 이상의 실수 비유전율을 유지하고, 3 GHz에서 20 정도의 가장 높은 허수 비유전율을 가진다. 이에 반해 LS22 모델은 100 MHz 이하에서 40 이상의 높은 실수 비유전율을 가지며, 120 MHz에서 30 정도의 가장 높은 허수 비유전율을 가진다. 결과적으로 LS26 모델은 수 백 MHz 이상의 고주파수용 흡수 소재이고, LS22 모델은 수 백 MHz 이하의 저주파수 대역의 흡수 소재임을 알 수 있다.

그림 5에 두께가 3 mm인 두 유전 흡수 소재의 차폐효과를 나타내었다. 흡수 소재이므로 도전성 차폐 소재에 비해 낮은 차폐 특성을 가진다. LS26 모델의 경우 주파수가 증가함에 따라 이론적인 분해법의 반사손실 $S E R S$ 은 감소하다가 약 4.5 GHz 이상의 주파수에서 흡수손실 $S E A S$ 보다 더 작은 값을 가진다. 이론적인 분해법의 흡수손실 $S E A S$ 은 주파수가 증가함에 따라 지속적으로 증가한다. 다중반사손실 $S E M S$ 은 약 1.6 GHz까지 (−) 값을 가지다가 그 이상의 주파수에서 (+) 값을 가지고 약 3.2 GHz까지 증가하다가 다시 감소한다. LS22 모델의 경우에는 약 1.7 GHz에서 반사손실과 흡수손실의 기여도가 역전되기 시작한다. 이처럼 유전 흡수 소재의 경우에도 주파수에 따른 이론적 분해법의 반사와 흡수손실이 도전성 차폐 소재의 그것들과 동일한 경향을 가짐을 알 수 있다.

그림 5. | Fig. 5. 두 유전 흡수 소재의 차폐효과와 그들의 성분 비교 | Comparison of shielding effectiveness and their components of two dielectric absorbing materials.

Download Original Figure

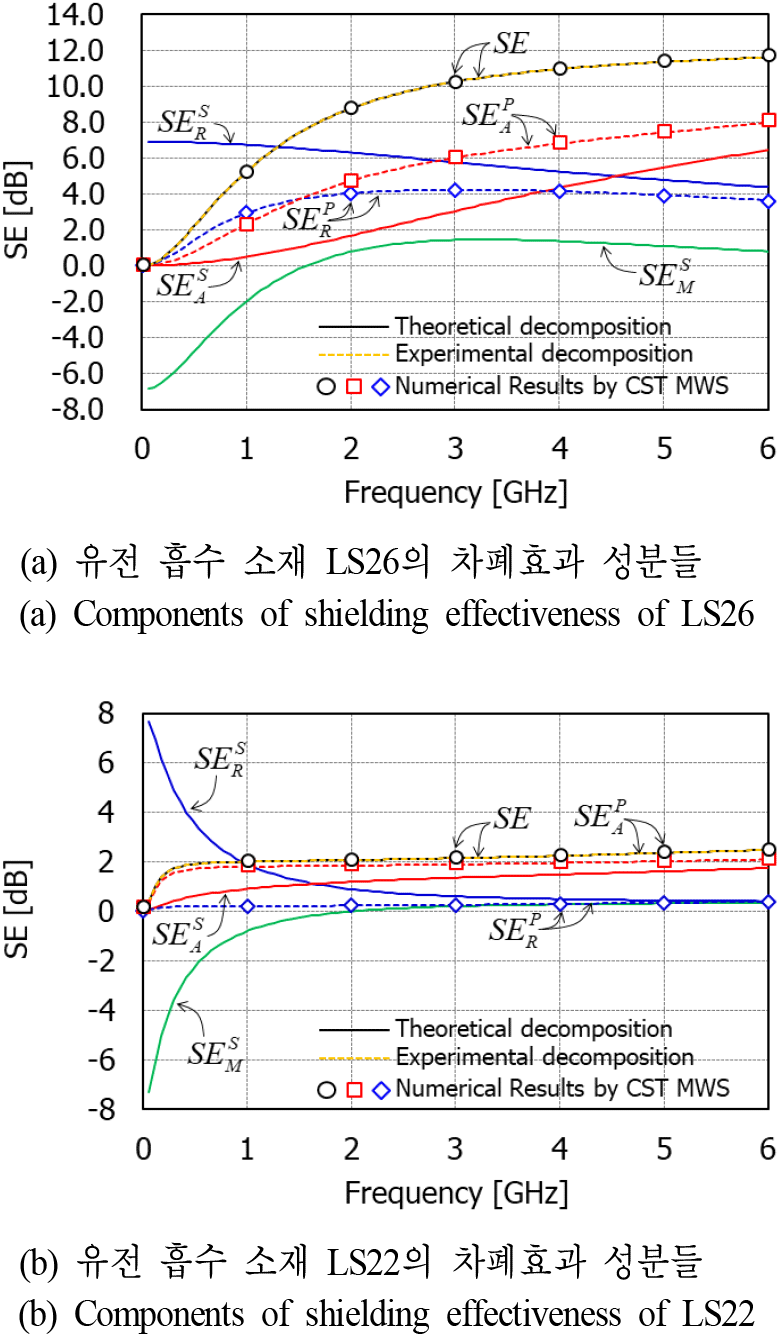
한편 실험적 분해법의 경우를 보면 유전 흡수 소재의 반사손실 $S E R P$ 과 흡수손실 $S E A P$ 은 주파수가 낮을 때 거의 0 dB인데, 그림 3에서의 도전성 차폐 소재와 다른 경향을 보임을 알 수 있다. LS26 모델에서 1.5 GHz까지는 반사손실이 더 빨리 증가하다가 이후의 주파수에서는 흡수손실이 더 빨리 증가한다. 흡수손실은 주파수가 증가할수록 지속적으로 증가하는 반면 반사손실은 3 GHz에서 최댓값을 가지고 그 이후 주파수에서는 감소한다. 결과적으로 LS26 모델의 경우 1.5 GHz 이상의 주파수 대역에서는 흡수손실의 차폐효과 기여도가 더 큼을 알 수 있다. 그 이유는 그림 4의 복소 비유전율 데이터에서 LS26 모델의 허수 비유전율이 GHz 대역에서 증가하기 때문이다.

LS22 모델의 경우 실험적 분해법에서의 흡수손실 $S E A P$ 은 매우 낮은 주파수에서부터 반사손실 $S E R P$ 보다 우세하다. 차폐효과가 낮지만 이는 대부분 흡수손실에 의해 발생함을 알 수 있다. 그 이유도 그림 4의 복소 비유전율 데이터에서 찾아볼 수 있는데, 120 MHz 이상에서 허수 비유전율이 실수 비유전율보다 더 큰 값을 가지기 때문이다. 두 유전 흡수 소재에 대해서 식 (13) 및 식 (14)로부터 계산한 실험적인 분해법의 결과는 CST MWS 시뮬레이션 결과와 거의 일치함을 알 수 있다.

앞서 Ⅳ절에서는 이론적인 분해법의 반사 및 흡수손실과 실험적인 분해법의 근사식(식 (21) 및 식 (22))과의 관계를 유도하였다. 이는 S₁₁의 위상각(θ)이 거의 0일 때 실험적인 분해법의 근사식과 이론적인 분해법의 반사 $S E R S$ 및 흡수손실 $S E A S$ 과의 관계를 잘 설명해 준다. 따라서 θ에 따라 실험적인 분해법의 반사손실 $S E R P$ 과 흡수손실 $S E A P$ 이 그들의 근사식과의 차이를 분석할 필요가 있다.

그림 6에서는 두 도전성 차폐 소재에 대한 실험적인 분해법의 반사 및 흡수손실과 그들의 근사식의 계산결과를 비교하였다. 또한 S₁₁의 위상각(θ) 함수인 cos2θ 값도 같이 그렸다. 다시 말하지만 cos2θ=1이 되면 실험적 분해법의 반사와 흡수손실에 대한 근사식은 그들의 정확한 식과 일치한다. σ=10⁴ S/m인 도전성 소재의 경우 6 GHz까지 cos2θ는 거의 1이다. 그래서 실험적인 분해법의 반사 및 흡수손실에서 정확한 식과 근사식의 값이 거의 동일하다. 주파수가 증가하면 그 차이가 증가하지만 6 GHz에서 1.5 dB 이내의 오차를 가진다. 정확한 식의 값에 비해 근사식의 반사손실은 약간 더 작고, 흡수손실은 약간 더 크다. σ=10 S/m인 소재의 경우 주파수가 증가할수록 cos2θ 값이 조금씩 줄어들어 6 GHz에서 약 0.8이 되었다. 정확한 식과 근사식 간의 오차는 1.5 dB로 σ=10⁴ S/m인 소재의 그것과 비슷하지만 낮은 차폐효과로 인해 차폐효과 대비 오차의 비율은 더 증가하였음을 알 수 있다.

그림 6. | Fig. 6. 두 도전성 소재의 실험적인 차폐효과 성분들 | Experimental SE components of two conductive materials.

Download Original Figure

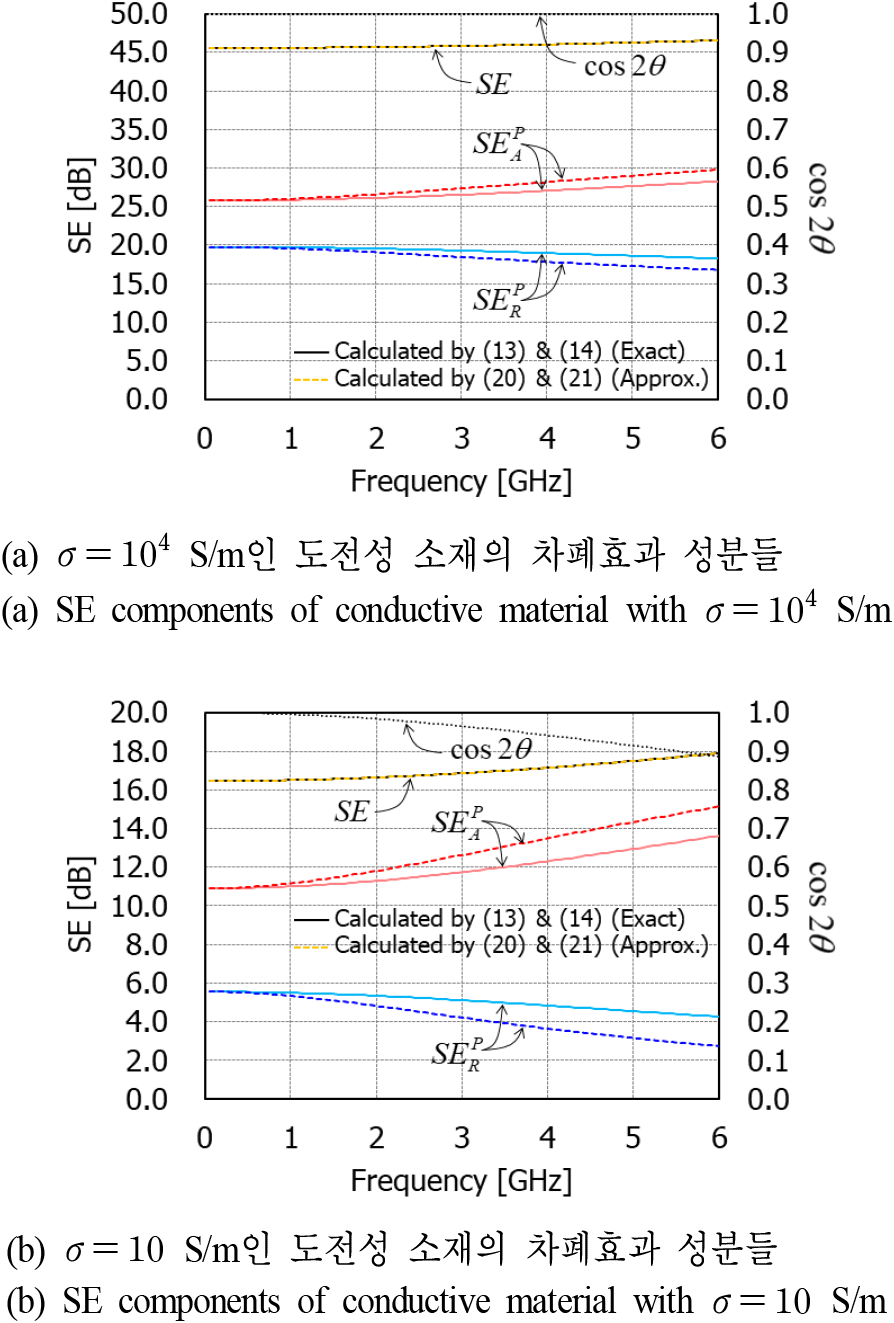
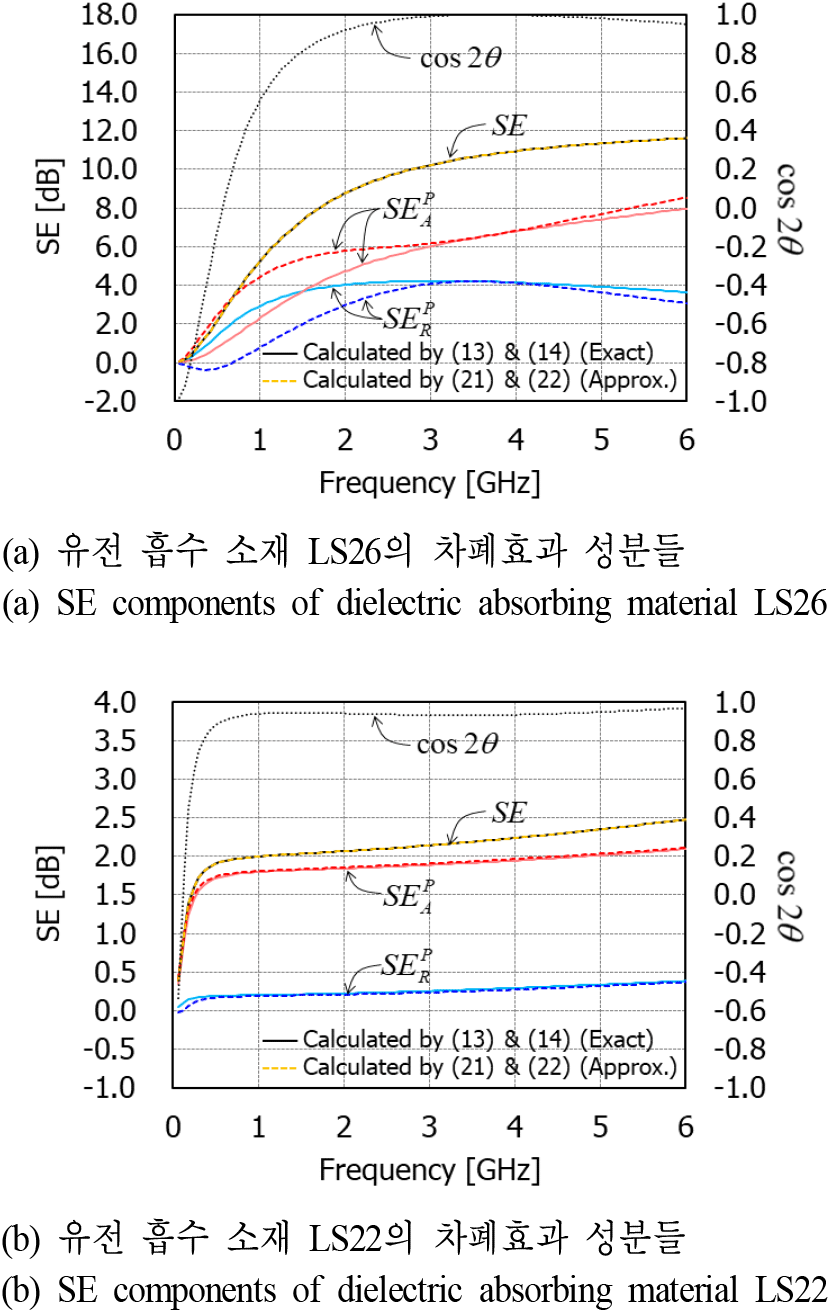
그림 7에서는 두 유전 흡수 소재에 대한 실험적인 분해법의 정확한 식과 근사식의 오차를 비교하였다. LS26 모델의 경우 2 GHz 이하의 주파수 대역에서는 cos2θ 값이 0.9보다 작아져 오차가 수 dB로 증가한다. 그러나 3 GHz 이상의 주파수 대역에서는 오차가 크지 않다. LS22 모델의 경우 약 500 MHz 이상의 주파수 대역에서는 cos2θ 값이 0.9보다 커져 반사손실 $S E R P$ 과 흡수손실 $S E A P$ 에 대한 정확한 식과 근사식의 값이 거의 일치하였다.

그림 7. | Fig. 7. 두 유전 흡수 소재의 실험적인 차폐효과 성분들 | Experimental SE components of two dielectric absorbing materials.

Download Original Figure

Ⅵ. 결 론

본 논문에서는 소재의 평면파 차폐효과에 대한 Schelkunoff의 이론적인 분해법인 반사손실 $S E R S$ , 흡수손실 $S E A S$ , 다중반사손실 $S E M S$ 과 전력균형원리를 토대로 한 실험적인 분해법에서의 반사손실 $S E R P$ 과 흡수손실 $S E A P$ 의 관계를 규명하였다. 이론적인 분해법에서의 반사손실과 흡수손실은 실험적인 분해법에서의 그것과 다름을 수학적으로 확인하였고, 특정 조건에서 실험적인 분해법의 근사식을 이용하여 이론적인 분해법과의 관계를 엄밀하게 유도하였다. 도전성 차폐 소재와 유전 흡수 소재에 대해서 주어진 물성을 이용하여 이론적인 차폐효과를 계산하였고 반사와 흡수에 의한 차폐효과 기여도를 비교하였다. 또한 3차원 수치해석을 통해 실험적 분해법에서 반사와 흡수의 차폐효과 기여도를 계산하였고 해석적으로 계산한 값과 비교하여 정확성을 확인하였다.

References

[1].

S. A. Schelkunoff, Electromagnetic Waves, New York, NY, David Van Nostrand Company, 1943.

[2].

H. H. Park, J. H. Kwon, and C. H. Hyoung, "Analytic comparison of reflection-based and transmission-based absorptances for planar materials," The Journal of Korean Institute of Electromagnetic Engineering and Science, vol. 35, no. 3, pp. 245-248, Mar. 2024.

[3].

M. H. Al-Saleh, U. Sundararaj, "Electromagnetic interference shielding mechanisms of CNT/polymer composites," Carbon, vol. 47, no. 7, pp. 1738-1746, Jun. 2009.

[4].

D. Munalli, G. Dimitrakis, D. Chronopoulos, S. Greedy, and A. Long, "Electromagnetic shielding effectiveness of carbon fibre reinforced composites," Composites Part B: Engineering, vol. 173, p. 106906, Sep. 2019.

[5].

X. Jia, Y. Li, B. Shen, and W. Zheng, "Evaluation, fabrication and dynamic performance regulation of green EMI-shielding materials with low reflectivity: A review," Composites Part B: Engineering, vol. 233, p. 109652, Mar. 2022.

[6].

C. R. Paul, R. C. Scully, and M. A. Steffka Introduction to Electromagnetic Compatibility, 2nd ed. Hoboken, NJ, Wiley, 2006.

[7].

H. W. Ott, Electromagnetic Compatibility Engineering, Hoboken, NJ, John Wiley & Sons, 2011.

[8].

A. J. McDowell, T. H. Hubing, "Analysis and comparison of plane wave shielding effectiveness decompositions," IEEE Transactions on Electromagnetic Compatibility, vol. 56, no. 6, pp. 1711-1714, Dec. 2014.

[9].

M. Peng, F. Qin, "Clarification of basic concepts for electromagnetic interference shielding effectiveness," Journal of Applied Physics, vol. 130, no. 22, p. 225108, Dec. 2021.

[10].

ASTM International, Standard Test Method for Measuring the Electromagnetic Shielding Effectiveness of Planar Materials, ASTM Standard D4935, 2010.

[11].

CST Microwave Studio(MWS), "Dassault systèmes virtual worlds help you improve real life," 2024. Available: https://www.3ds.com/products/simulia/cst-studio-suite

[12].

Laird, "EccosorbTM LS," Nov. 2024. Available: https://www.laird.com/products/absorbers/microwave-absorbing-foams/single-layer-foams/eccosorb-ls

Notes

박 현 호 [수원대학교/교수]

jkiees-35-12-997-i1

https://orcid.org/0000-0001-8518-1151
1999년 8월: 한국과학기술원 전기및전자공학과 (공학박사)
1999년 9월: 한국전자통신연구원(ETRI) 선임연구원
2006년 6월: 삼성전자 글로벌기술센터 수석연구원
2012년 9월~현재: 수원대학교 전기전자공학부 교수
[주 관심분야] EMI/EMC 대책 기술, 전자파 차폐 기술, 전자파 해석 기술, SI/PI 설계 기술

소재의 평면파 차폐효과에 대한 이론적 및 실험적 분해법 비교

요 약

Abstract

Ⅰ. 서 론

Ⅱ. 차폐효과의 이론적인 분해법[1],[6],[7]

Ⅲ. 차폐효과의 실험적인 분해법[2],[8],[9]

Ⅳ. 두 분해법의 해석적인 관계

Ⅴ. 계산 결과 및 수치해석 검증

Ⅵ. 결 론

References

Notes

Ⅱ. 차폐효과의 이론적인 분해법^[1],[6],[7]

Ⅲ. 차폐효과의 실험적인 분해법^[2],[8],[9]