논문/REGULAR PAPER
mmWave FMCW MIMO 레이다를 이용한 3차원 공간에서의 실내 다중 표적 추적을 위한 반복 알고리즘
마살라므보이질요웰

, 오동현

, 김형주
*
, 정병장
*
, 한정훈
**,†
Iterative Algorithm for Indoor Multiple Target Tracking in 3D Space Using mmWave FMCW MIMO Radar
MASSALA MBOYI Gilles Yowel

, Dong-Hyun Oh

, Hyung-ju Kim
*
, Byung-Jang Jeong
*
, Jung-Hoon Han
**,†
Department of Telecommunication Engineering, Jeju National University
*Radio Research Division, ETRI
**Department of Electrical and Electronic Engineering, Korea Aerospace University
© Copyright 2024 The Korean Institute of Electromagnetic Engineering and Science. This is an Open-Access article distributed under the terms of the
Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits
unrestricted non-commercial use, distribution, and reproduction in any
medium, provided the original work is properly cited.
Received: Jul 11, 2024; Revised: Aug 08, 2024; Accepted: Sep 16, 2024
Published Online: Dec 31, 2024
요 약
본 연구에서는 우선 동일한 거리 내에 위치한 여러 표적이 있는 시나리오에서 range-azimuth 및 range-elevation 각 평면에서 별도로 식별된 표적을 상호 매칭하는 문제를 다룬다. 레이다 영상에서 범위-방위각(range-azimuth) 및 범위-고각(range-elevation) 맵은 탐지된 물체의 공간적 위치를 나타내는 데 사용된다. 범위-방위각 맵은 목표물의 거리(범위)와 수평 방향(방위각)을 표시하여 환경의 상단 뷰를 제공한다. 범위-고각 맵은 목표물의 거리와 수직 각도(고각)를 나타내어 물체가 레이다에 대해 얼마나 높거나 낮은지를 측정할 수 있는 측면 뷰를 제공한다. 그리고 비선형 가상 안테나 배열로 구성된 레이다 데이터 큐브에서 거리, 방위 및 고도 정보를 재귀적으로 추출하는 알고리즘을 응용하여 3-D 위치 추정을 가능하게 하는 해결 방안을 제안한다. 제안하는 반복 재귀 추출 과정은 레이다 데이터 큐브의 모든 프레임에 체계적으로 적용되어 시간 차원 영역에서 정보를 포착하고, 실시간 실내 추적을 수행하였다. 실험과 측정을 통해 단일 표적 시나리오와 지속적으로 앞뒤로 움직이는 두 표적들에 대한 시나리오에서 정확한 추적을 구현하여, 제안하는 접근 방식의 성능을 입증하였다.
Abstract
In this study, we address the challenge of matching separately identified targets in the range-azimuth and range-elevation planes, particularly in scenarios involving multiple targets located in the same range. Range-azimuth and range-elevation maps were used in the radar imagery to represent the spatial positions of the detected objects. A range-azimuth map displays the distance (range) and horizontal direction (azimuth) of the targets, providing a top-down view of the environment. A range-elevation map shows the distance and vertical angle (elevation) of the targets, offering a side view to determine how high or low the objects are relative to the radar. We propose a solution that enables 3D positioning by employing an algorithm designed to recursively extract the range, azimuth, and elevation information from a radar data cube built with a nonlinear virtual antenna array. This iterative process was systematically applied across all the frames of the radar data cube to capture the temporal dimensions and perform real-time indoor tracking. Through comprehensive empirical measurements, we demonstrate the efficacy of our approach, achieving precise tracking in scenarios involving a single target and two targets in a permanent back-and-forth movement.
Keywords: 3-D Positioning; Frequency Modulated Continuous Wave (FMCW) Radar; Millimeter-Wave; Radar Data Cube Processing
I. 서 론
FMCW(fequency-modulated continues wave) MIMO(multiple-input multiple-output) 레이다 기술은 실외 및 실내 환경에서 사람과 물체 감지에 널리 사용된다. 이 다용도 센서는 고급 운전자 보조 시스템 및 자율 주행을 위한 미래 자동차 분야, 낮은 가시성 환경에서 로봇 내비게이션을 위한 로봇 공학 분야, 사람의 심박수 원격 모니터링을 위한 의료 분야, 표적 분류 및 위치 파악을 위한 컴퓨터 비전 분야 등 다양한 영역에서 응용 기술로 활용된다[1]~[4].
최근 몇 십 년간 레이다 효율성 연구는 큰 발전을 이루었으며, 이동 표적 탐지[5], 입사각(DoA)의 정확한 추정[6], 지상 이동 표적 이미지화[7], 안테나 패턴 합성[8],[9]과 같은 도전 과제들을 해결하기 위한 다양한 노력이 이루어졌다. 이러한 발전은 다양한 응용 분야에서 레이다 성능을 향상시키고, 보다 정밀하고 신뢰성 높은 시스템으로 이어지도록 하는 데 중점을 두고 있다.
FMCW MIMO 시스템의 동작은 밀리미터파(mmWave) 스펙트럼 내에서 저전력 전자기 펄스의 주기적인 전송으로 시작된다. 시분할 다중화 다중 입력 다중 출력(TDM [time division multiplexing]MIMO) 처리를 통해 레이다 시스템은 다중 안테나를 사용하여 공간 다이버시티를 얻고 신호를 순차적으로 송수신하여 표적 정보를 획득할 수 있다[10]. 이 기술은 복잡한 다중 경로 환경에서 표적을 식별하고 특성화하는 레이다의 능력을 향상시켜, 표적 검출 및 위치 결정에 있어서 정확성과 신뢰성 향상에 기여한다.
실내에서 레이다 시스템을 사용한 표적의 3D 매핑은 복잡한 환경 내에서 물체나 사람을 정확하게 탐지, 추적 및 식별하는 데 필수적이다. 이를 통해 표적의 위치, 크기, 이동 등 3차원(거리, 방위각, 고각)에서의 세부적인 공간 정보를 제공하여 상황 인식을 향상시키고, 보안 및 노인 돌봄과 같은 응용 분야에서 안전성을 개선하며, 정밀한 제스처 인식 및 스마트 빌딩에서의 효율적인 점유 감지와 같은 고급 기능을 가능하게 한다. 최적의 위치 추정 성능은 레이다에 의해 수신된 펄스에서 높은 신호 대 잡음비(SNR, signal-to-noise ratio)를 유지하는 것이 중요하다. SNR은 레이다 단면적(RCS, radar cross-section)과 같은 표적별 매개변수뿐만 아니라 잡음 및 간섭과 같은 환경 요인과도 복합적으로 관련되어 있다[11]~[13]. RCS는 표적이 레이다 시스템을 향해 반사하는 전자기파 에너지의 양을 정량화한다. 본질적으로 RCS는 레이다 화면에서 표적의 가시성을 나타내는 지표이다[14],[15].
실내 측위는 주로 벽 반사로 인한 다중 경로 효과와 실험 공간 내의 다른 전자 장치들의 간섭으로 인해 실외 시나리오와 비교하여 풀어야할 많은 문제들을 제시한다[16]~[20]. 다양한 레이다 운영 환경, 특히 실내 환경에서 FMCW MIMO 레이다 기술의 효율성을 향상시키기 위한 다양한 연구들이 진행되었다[21]~[23]. 하지만 거리-방위 평면 내에서 2-D 고도 요소의 추출을 효과적으로 얻어는 내는 방법에 대한 해결책도 여전히 필요하다.
실내 표적의 3D 공간에서의 위치 추적을 달성하기 위해 수많은 노력이 기울여져 왔다[24]~[26]. 그러나 이전 연구들은 3D 위치 추적을 위해 별도의 거리-방위각 맵과 거리-고각 맵을 사용했다. 단일 표적의 경우, 두 맵 간의 공통 매개변수로서 거리를 활용해 모든 위치 정보를 추출할 수 있다. 하지만 여러 표적이 동일한 거리에 위치할 경우, 매칭이 불가능해져 실시간 추적이 어려워진다. 이러한 문제는 주로 방위각 정보와 고각 정보 간의 대응 관계가 부족하기 때문에 발생하며, 이는 모든 표적에 대해 동일하게 유지되는 공통 매개변수로 해결할 수 없다.
본 논문은 거리-방위 및 거리-고도 평면에 매핑된 단일 3D 맵 내에서 표적을 상호 일치시키는 방법에 대해서 제시하였다. 거리 프로파일의 거리 정보, 거리-방위 맵의 방위 정보, 방위-고도 맵의 고도 정보를 재귀적으로 추출하는 반복 알고리즘을 제안한다. 그리고 실제로 실험과 측정을 수행하여 3-D 맵 내에서 표적 위치 추정을 효과적으로 수행할 수 있다.
Ⅱ. 레이다 시스템의 구성
FMCW MIMO 레이다 시스템은 시간에 따라 다른 주파수를 가진 연속적인 전자기파를 전송함으로써 작동한다. 레이다의 안테나는 전파 신호를 송수신하여 시야에 있는 여러 표적으로부터의 반사파를 감지하고 처리한다. 레이다는 반환된 신호를 분석하여 거리, 방위각, 고도 및 속도와 같은 정보를 얻어낼 수 있지만, 주변 환경에 대한 정보를 잡음의 형태로 동시에 포함하고 있다. 이와 같은 정보들을 적절히 신호 처리하여 표적 인식 및 추적과 같은 응용 기술의 성능을 향상시킨다.
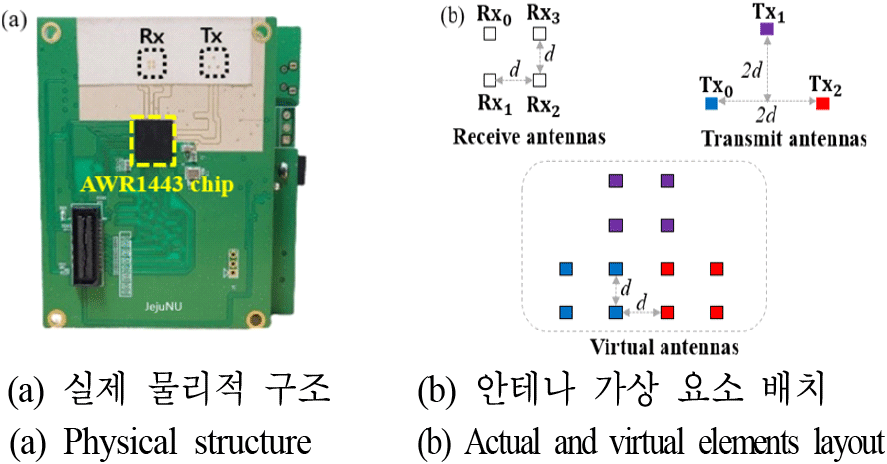
그림 1은 본 연구실에서 재설계한 레이다 안테나 시스템을 보여준다. 정사각형 형태로 배열된 4개의 수신 안테나와 이등변 삼각형 구성으로 배치된 3개의 송신 안테나를 특징으로 한다. 수신 안테나의 요소 간 간격 d는 전송 사용 신호 대역의 중심주파수 파장의 반에 해당한다[10]. 결과적으로 가상 안테나 구조는 방위각(수평) 및 고도(수직) 방향 모두에 걸쳐 안테나 요소들이 균형 잡힌 분포가 되도록 설계되었다. 즉, 제한된 송수신 안테나 개수들을 활용하여 최대한의 방위 및 고도 방향으로 해상도를 동일하게 얻을 수 있도록 배치하였다. 다음 방정식과 같이 방위 및 고도 방향 두 차원에서 동일한 각도 분해능을 얻을 수 있다.
여기서 λ은 송신 신호의 파장, NR은 수신 소자의 개수, θ는 수신 신호의 도달 방향(DoA)이다. 본 안테나 구성의 경우 수신 소자가 4개이므로 방위 및 고도의 모든 방향에서 각도 분해능은 Δθ=29°가 된다. 구성된 안테나 요소의 배치는 방위 및 고도 방향에 대한 표적 인식을 동시에 가능하게 할 수 있다. 하지만 거리-방위와 거리-고각에 대한 정보를 각각 얻기 때문에, 신호처리에서 방위각상의 표적 점들이 고각에서는 어떠한 점에 해당하는지에 대한 상호 매칭 문제가 해결되어야 한다.
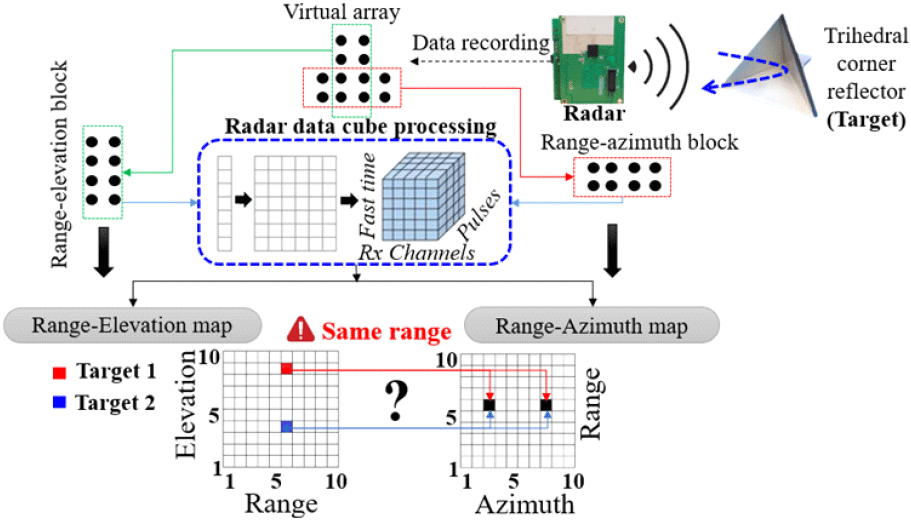
표적 매칭의 문제 해결에 대한 정의는 그림 2에 나타나있다. FMCW MIMO 레이다는 산란 점들의 움직임의 장면들을 포착한다. 데이터 처리에서 수직 및 수평 가상 배열 요소를 저장하는 데이터 블록을 활용하면 거리-고도 및 거리-방위 평면에서 각각 표적을 매핑할 수 있다. 각 거리 블록에 의해 수집된 원시 데이터는 레이다 데이터 큐브라는 형태로 구성된다. 이 구조는 공간 및 시간 차원에서 기록된 데이터를 더 잘 표현할 수 있게 하여 표적 위치 정보를 추출하기 위한 후속 처리를 도움이 된다. ri은 범위, θi는 고도, ϕi는 레이다에 의해 감지된 i번째의 방위각이다. 이러한 매개 변수는 거리-방위 및 거리-고도 맵을 통해 추출할 수 있다.
그림 2. | Fig. 2.
다수의 3차원 표적들에 대한 위치 정보를 주어진 가상 배열을 이용하여 매칭하는 방안 | Illustration of the problem of multiple targets matching.
Download Original Figure
레이다의 시야 내에 단일 표적이 존재하는 시나리오에서 거리는 두 맵에서 방위 및 고도 구성 요소들을 추출하기 위한 공유 매개 변수 역할을 하여, 3차원 공간에서 정확한 표적 위치 지정을 가능하게 한다. 그럼에도 불구하고 여러 표적, 특히 동일한 범위에 위치한 표적을 포함하는 상황에서는 두 표적의 단순한 경우에 대해 그림 2에 나타난 바와 같이 이 접근 방식을 통한 방위 및 고도 정보의 매칭이 불가능해진다. 거리-고각 맵에서는 두 개의 표적(빨간색과 파란색)이 서로 다른 고각 빈에 위치하지만 동일한 거리에 있는 것을 관찰할 수 있다. 이 장면은 거리-방위각 맵에서도 나타나며, 여기서 표적들은 동일한 거리에 있지만 다른 방위각 빈을 차지하고 있다. 이 특정 시나리오에서는, 거리-고각 맵과 거리-방위각 맵 간에 빨간색과 파란색 표적의 위치를 일치시키는 것이 고각과 방위각 빈의 차이로 인해 불가능해져, 정확한 표적 연관이 어렵다. 이 문제의 근본적인 원인은 방위각과 고각 간의 정보 일치가 없기 때문이며, 모든 표적에 대해 동일한 공통 매개변수로는 이를 해결할 수 없다. 이는 ri=rj(i≠j)의 경우 2개 이상의 표적에 대해 해결해야한 문제이고, 이를 극복하기 위하여 다음의 방안을 제안하였다.
Ⅲ. 제안된 신호 처리 과정
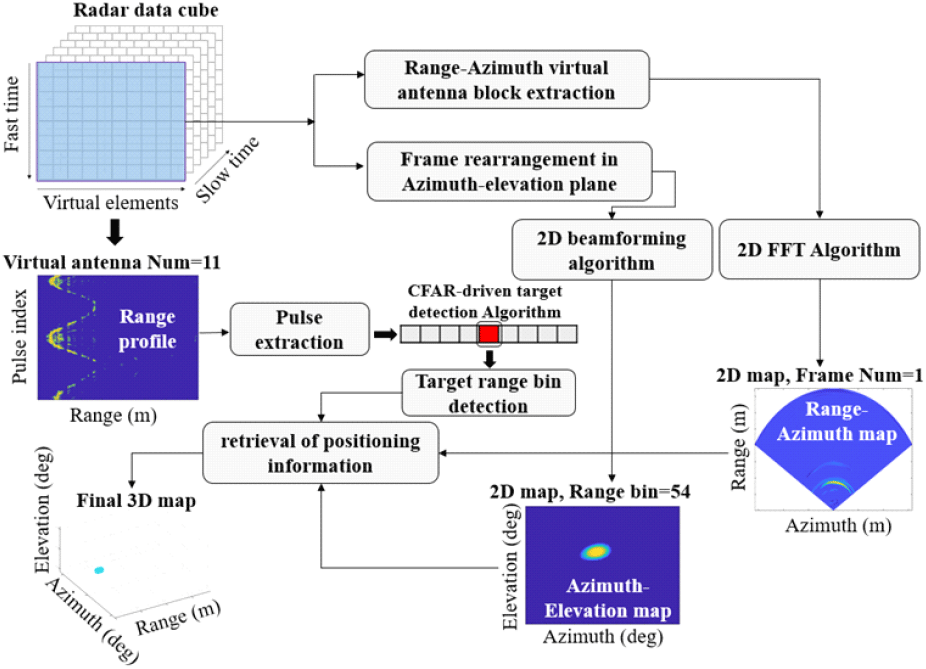
앞서 언급한 문제를 극복하기 위해 거리 프로파일에서 거리 정보를 연속적으로 추출한 다음, 거리-방위 맵에서 방위 성분을 추출하고 마지막으로 방위-고도 맵에서 고도 성분을 추출하는 과정을 제안한다. 해당 개념은 그림 3에 나타내었다. 먼저 원시 데이터를 저장한 후 레이다 데이터 큐브를 컴팩트한 구조로 재구성하였다. 첫 번째 축에는 하나의 전송 펄스의 후방 산란 신호가 저장되고, 두 번째 축에는 다른 수신 요소의 산란 수신 신호가 저장된다. 세 번째 축은 여러 전송 펄스의 산란 수신 신호를 저장한 것이다. FMCW 레이다 시스템은 시간에 따라 선형적으로 증가하는 각도 주파수를 특징으로 하는 주기적인 처프(chirp) 신호를 송신한다. 한 번의 처프 동안 방사되는 신호는 수학적으로 식 (2)와 같이 표현할 수 있다.
그림 3. | Fig. 3.
레이다 데이터 큐브의 한 프레임에서 재귀적으로 위치결정 파라미터를 추출하기 위한 제안된 신호처리과정 | Proposed signal processing workflow to extract recursively positioning parameters in one frame of the radar data cube.
Download Original Figure
여기서 fc는 전송된 신호의 중심 주파수를 나타내고 β는 챱(chirp) 속도를 나타내고, t는 빠른 시간(fast-time)을 의미한다. 각 전송 주기 동안 레이다 신호의 주파수는 지정된 범위에 걸쳐 변조된다. 이 변조는 주파수가 일정한 속도로 변하는 선형 주파수 변화 또는 비선형 주파수 변화로 인해 더 복잡한 패턴을 나타낼 수 있다. 주파수 스위프(sweep)에 할당된 지속 시간은 일반적으로 펄스 반복 간격(PRI)으로 불린다. 이 매개 변수는 레이다의 거리 분해능을 결정하는 역할을 한다. 전송은 L번 연속 처프에 걸쳐 반복되므로 수신 신호와 전송 신호를 결합하여 반송파 주파수 성분을 제거한다. IF(intermediate frequency) 대역의 결과 신호는 수학적으로 2차원 지수 함수로 표현될 수 있다[27].
n과 l은 각각 처프 내의 샘플링 인덱스와 처프 인덱스를 나타낸다. 또한, r과 v는 표적의 거리와 속도를 나타내고, Ts는 샘플링 주기를 나타내며, λ은 송신 신호의 파장을 나타내고, ϕ는 위상을 나타낸다.
균일한 선형 배열(ULA)을 사용하는 안테나 시스템을 사용하여 도달각(AoA)을 추정할 수 있다. 수신 신호의 입사각이 θ이고 안테나 간격이 d인 경우 인접한 안테나 간의 위상차는
로 나타낼 수 있다. 이 항과 식 (3)을 결합하여 3차원 IF 대역 신호를 생성할 수 있으며, 수학적으로는 식 (5)와 같이 표시된다[27].
여기서 k는 안테나 인덱스를 나타내고 K는 수신 안테나의 총 개수를 나타낸다. 결국, 이 식은 레이다 데이터 큐브의 수학적 표현이 된다.
빠른 시간 축에 FFT 알고리즘을 적용하면 거리 정보를 추출할 수 있다. 수신 채널에 적용하면 각도 정보(방위각 및/또는 고각)를 얻을 수 있으며, 느린 시간 축에 적용하면 도플러 정보를 추출할 수 있습니다. 이는 그림 3에 나타나 있다. 적절한 방향으로 FFT 알고리즘을 적용하면 그림 3과 같이 범위, 방위 및 고도 각도, 도플러 정보를 추출할 수 있다. 하나의 가상 요소에 의해 수집된 모든 데이터가 추출되고 FFT 알고리즘이 빠른(fast) 시간 축을 따라 적용되어 거리 프로파일을 얻는다. 마찬가지로 한 프레임의 데이터가 추출되고 빠른 시간과 가상 요소 축을 따라 2D-FFT가 적용되어 거리-각도 맵을 얻는다. 프레임 차분 기반 배경 제거 및 CFAR 알고리즘이 거리 프로파일에 연속적으로 적용되어 클러터 제거 및 대상 거리 빈(bin) 검출을 할 수 있다.
본 연구에서는 cell averaging greatest of CFAR(CAGO-CFAR) 알고리즘을 사용했다. CAGO-CFAR 알고리즘은 참조 셀로 알려진 특정 지역에서 레이다 신호의 통계적 특성을 평가하여 구현된다. 이 참조 셀은 탐지를 위한 임계값을 설정하는 데 중요한 매개변수 역할을 한다. 이를 고려하여 CFAR 알고리즘은 참조 셀 내의 평균 전력을 계산하고 노이즈 레벨을 결정하며 대상 셀의 신호 전력을 이 임계값과 비교하여 배경 노이즈의 영향을 완화하면서 잠재적인 대상을 식별한다. 탐지는 테스트 대상 셀의 전력 신호(CUT)가 CAGO-CFAR 임계값보다 높으면 발생된다. 이 임계값은 식 (6)으로 정의된다[28].
여기서 N은 배경 잡음을 추정하기 위해 사용되는 참조 셀의 총 수를 나타내며, Xn은 n번째 참조 셀의 신호 전력을 의미한다. CAGO-CFAR은 레이다 시스템에서 다중 경로의 영향을 완화하기 위해 잡음 환경에 따라 탐지 임계값을 동적으로 조정하여, 불필요한 반사로 인한 오탐지를 줄이다. MTI는 정지된 물체와 클러터를 필터링하여 이동하는 표적에 초점을 맞추고 다중 경로로 인해 발생한 신호를 억제함으로써 표적 탐지를 향상시킨다. 이 알고리즘들은 함께 복잡한 실내 환경에서 레이다 표적 탐지 및 추적의 정확성과 신뢰성을 향상시킨다. 이러한 알고리즘들이 상당한 성과를 거두고 있음에도 불구하고, 이 문제는 여전히 레이다 신호 처리 분야에서 중요한 연구 과제로 남아 있다.
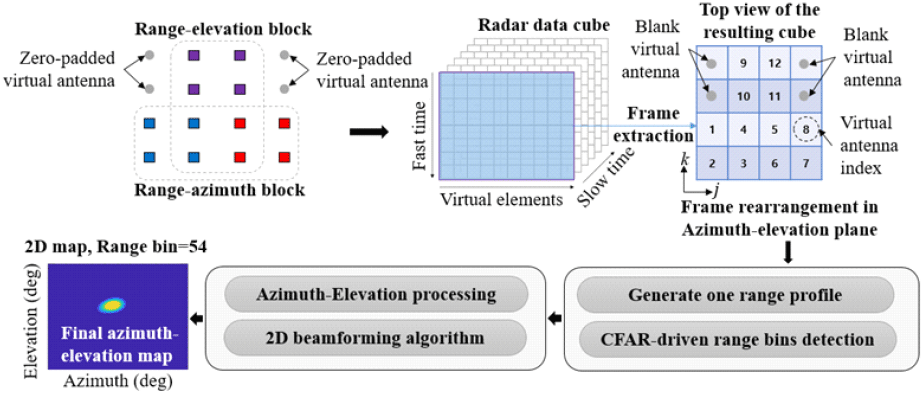
기존의 일반적인 레이다 데이터 큐브 구조는 방위각-고도 맵을 생성하기 위한 직접적인 메커니즘이 없다. 선행 단계는 그림 4와 같이 제안된 MIMO 구조에 맞게 레이다 데이터 큐브 프레임을 다시 형성해야한다. 실제로, 기존의 레이다 데이터 큐브는 모든 가상 요소를 수평 축에 정렬하는데, 이는 우리의 MIMO 배열 구조와 일치하지 않다. 이 구성에서는 방위각과 고각을 해결하기 위해 사용되는 안테나들이 단일 축에 혼합되어 있어 방위각-고각 매핑이 불가능하다. 프레임 재배열 과정은 기존의 레이다 데이터 큐브를 우리의 MIMO 배열 구조에 맞게 수정하여, 정확한 방위각-고각 매핑을 가능하게 하는 것이다. 가상 배열의 비선형적인 구성을 고려할 때, 직접 레이다 데이터 큐브 구성에 적합하지 않은 블랭크 가상 안테나를 도입하여 선형 배열을 구축하고 레이다 데이터 큐브를 생성한다. 빈 가상 안테나는 신호가 없는 요소를 의미한다. 이러한 요소를 추가하는 것은 원래의 가상 안테나 배열에 제로 패딩(zero-padding)을 수행하는 것을 포함한다. 이미징 알고리즘이 FFT에 의존하기 때문에, 이 제로 패딩은 스펙트럼 도메인에서 보간(interpolation)을 유도하며, 이를 통해 레이다 이미지의 시각적 품질이 향상되어, 보다 매끄러운 표현을 제공한다.
그림 4. | Fig. 4.
제안하는 방위-고도 평면의 표적을 매핑하기 위한 레이다 데이터 큐브 프레임 구성 전략 | Proposed radar data cube frame reformatting strategy to map targets in the azimuth-elevation plane.
Download Original Figure
그림 4는 기존 레이다 데이터 큐브의 가상 요소 인덱스를 나타내는 그리드 번호와 함께 레이다 데이터 큐브의 결과를 보여준다. 거리 프로파일에서 탐지된 거리 빈을 활용하여 CAGO-CFAR 알고리즘에 의해 식별된 목표에 해당하는 위치의 새로운 레이다 데이터 큐브에서 방위각-고도 데이터가 선택적으로 추출된다. 이후에 방위축을 따라 연속적인 방위각-FFT와 고도축을 따라 고도-FFT를 포함하는 2차원 빔포밍 알고리즘이 적용된다.
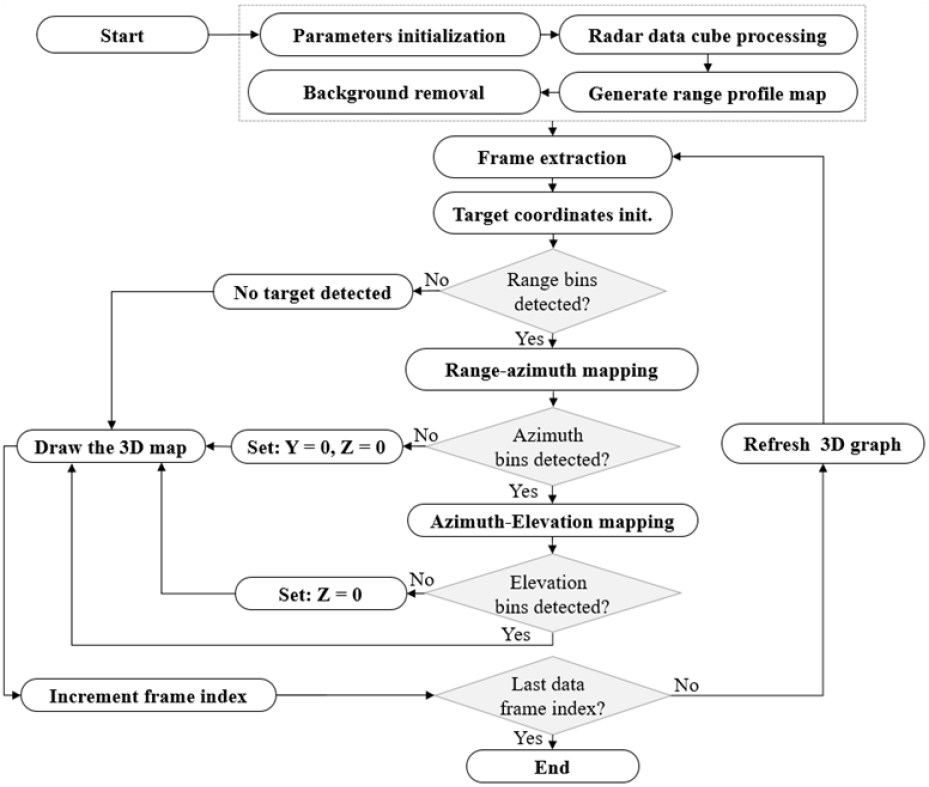
앞서 설명한 프로세스를 느린(slow) 시간 축을 따라 재귀적으로 반복하는 것은 시간적 구성 요소를 추출하고 실시간 추적을 구현하는 데 필수이다. 레이다 시스템의 각도 제한으로 인한 잠재적인 표적 오검출을 완화하기 위해 그림 5와 같이 주요 절차에 추가 조건을 더하였다. 거리 프로파일에서 목표가 감지되었지만 실제 방위각 구성 요소가 거리-방위 맵에서 제공되지 않는 경우 해당 거리 빈에서 레이다 가시선(Y=0, Z=0)을 따라 목표를 위치시킨다. 반대로 거리 빈과 방위각 구성 요소가 올바르게 추출되었지만 방위-고도 맵이 고도 구성 요소를 나타내지 못하는 경우에 표적이 원점(Z=0)에 있다고 가정한다. 다른 모든 경우에는 프레임에서 표적이 감지되지 않거나 모든 구성 요소들이 올바르게 추출된다. 이러한 조건은 재귀 알고리즘이 표적의 이전 상태를 추적하고 오탐지 시 미래 위치를 예측하는 메모리 메커니즘을 포함하지 않기 때문에 발생한다. 단일 표적에 대해 메모리 메커니즘을 구현하는 것은 간단하지만, 여러 표적이 있을 경우 복잡성이 크게 증가한다. 이러한 제한 사항은 향후 개선을 위해 고려해야 할 사항이다.
그림 5. | Fig. 5.
3차원 공간에서 표적 매핑을 위한 주요 흐름도 | Flowchart of the main procedure for target mapping in 3D space.
Download Original Figure
Ⅳ. 측정 결과
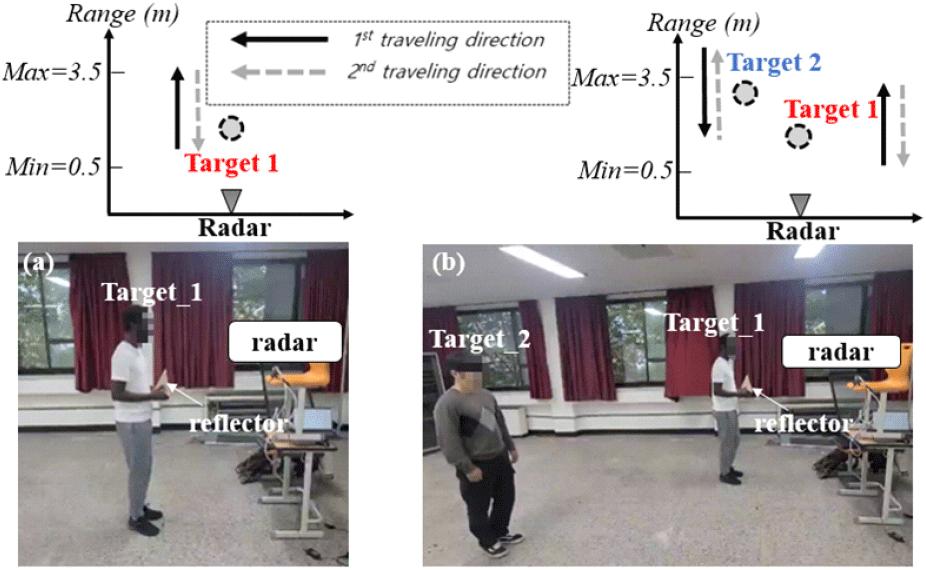
실험을 위하여 그림 6에 나타낸 두 가지 다른 시나리오에 대해서 진행하였다. 초기 시나리오에서는 반사판을 든 한 사람이 레이다 가시선 방향을 따라 앞뒤로 이동하였다. 두 번째 시나리오에서는 두 명의 사람이 서로 반대 방향으로 앞뒤로 교차 이동하였다. 한 사람만 반사판을 들고 있었다. 모든 실험에서 표적은 0.5 m에서 3.5 m 사이의 간격 내에서 움직였다. 그림 1에 제시된 레이다 시스템은 원시 데이터를 수집하는 데 사용되었다. 두 실험에 사용된 구성 요소들은 표 1에 나타내었다. 실내 환경에서 여러 개의 이동 대상을 추적하는 것은 다양한 요인으로 인해 복잡한 문제를 제시한다. 실내 공간은 좁고 다양한 난반사 환경을 포함하기 때문에 클러터 잡음이 많다. 또한 벽과 물체의 반사로 인한 다중 경로 효과는 대상의 위치 파악에 불확실성을 유발한다. 가구나 전자 장치와 같은 요소들이 존재하면 실제 대상을 배경 잡음과 구별하는 데 복잡성이 더해진다. 특히 실내와 같이 방해 요소가 있는 환경에서 제한된 시야와 신호의 불규칙적 수신은 지속적인 표적 추적을 방해한다. 이러한 모든 요인은 정확한 3D 실내 대상 추적을 구현하는 것을 어렵게 만든다.
그림 6. | Fig. 6.
실험의 구성 (a) 레이다의 시야를 따라 앞뒤로 이동하는 단일 표적, (b) 서로 반대 방향으로 이동하는 두 개의 표적 | Experiment setup (a) Single target moving back and forth along radar boresight, (b) Two targets moving in opposite directions.
Download Original Figure
표 1. | Table 1.
본 연구에 사용된 레이더 구성 | Radar configuration utilized in this study.
|
Parameter (unit) |
Value |
|
Start frequency, fc (GHz) |
77 |
|
Frequency limit high, fmax (GHz) |
81 |
|
Frequency slope, S (MHz/μs) |
30 |
|
Idle time (μs) |
100 |
|
TX start time (μs) |
0 |
|
ADC start time (μs) |
6 |
|
ADC samples |
256 |
|
Sample rate (ksps) |
10,000 |
|
Ramp end time (μs) |
60 |
|
Slow-time sampling frequency, fs (Hz) |
20 |
Download Excel Table
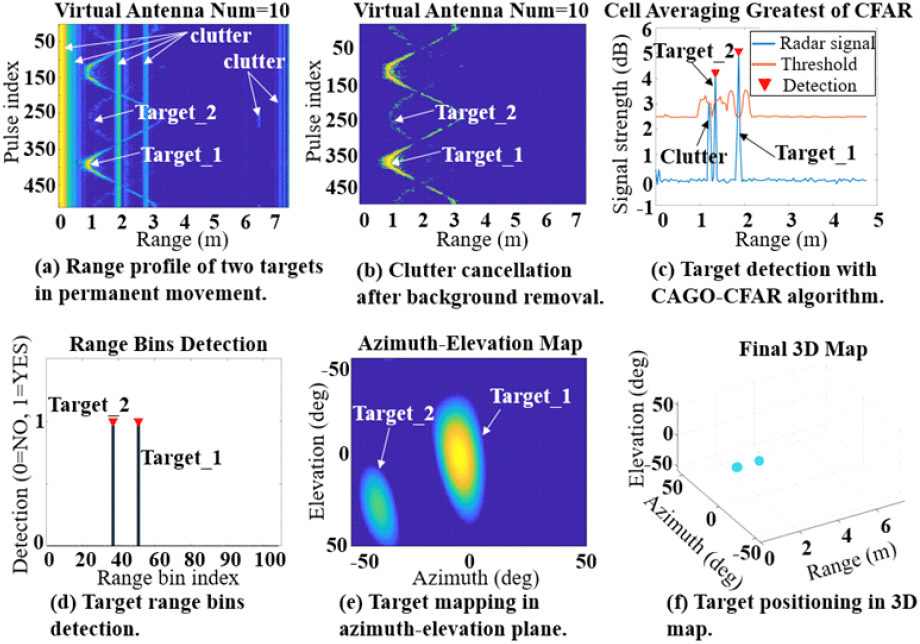
제안된 신호 처리 과정의 각 단계의 결과는 서로 반대 방향으로 이동하는 두 개의 표적에 대한 시나리오에 초점을 맞춰 그림 7에 나나타내었다. 거리 프로파일은 이동하는 표적에 해당하는 반대 위상을 가진 두 개의 정현 패턴을 보여주며, 여기서 더 강한 신호는 반사판 표적과 관련이 있다. 이러한 정현 곡선은 최소 약 0.5 m에서 최대 약 3.5 m 사이에서 진동한다. 표적이 레이다에 가까울 때 전력 신호가 강하고 표적이 멀어지면 점점 약해진다. 하지만 표적보다 더 강한 신호를 반사하는 클러터의 영향이 커서 잠재적으로 표적 감지를 방해한다. 배경 제거 알고리즘을 적용하면 클러터가 효과적으로 제거되어 관심 있는 표적만 거리 프로파일에 남게 된다. 그 후 CAGO-CFAR 알고리즘을 사용하여 표적의 정확한 위치를 감지한다. 거리 빈은 거리 해상도 요인에 의해 표적의 위치에 비례하기 때문에 쉽게 추정되었다. 그런 다음 계산된 거리 빈은 2D 빔포밍 알고리즘 적용을 위한 영역을 지정하는 데 사용되어 방위-고도 맵을 생성한다. 실험 수행 초기에 반사판 표적 1이 레이다에 더 가까웠음을 그림 6(b)에서 알 수 있다. 이는 그림 7(e)에 묘사된 방위-고도 맵의 첫 번째 프레임에서 약 0°의 강한 전력 신호와 관련이 있다. 두 번째 표적은 멀리 떨어져 있고 반사판이 없었기 때문에 방위-고도 맵에서 약한 전력 신호가 나타났다.
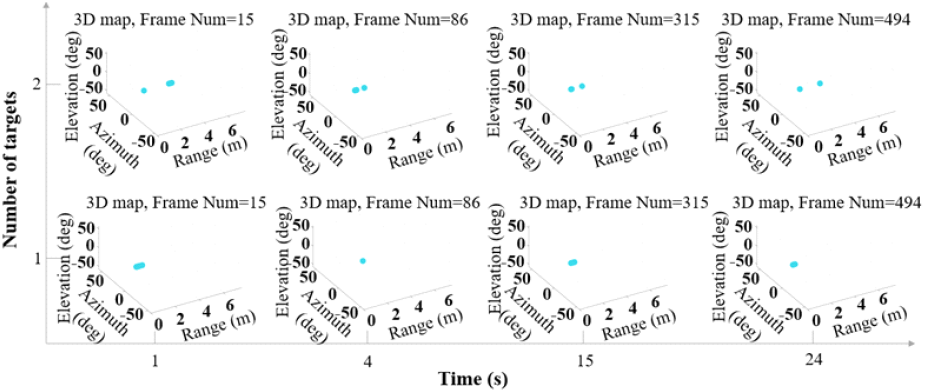
실험의 원시 데이터는 25초 간격에 걸쳐 수신되었으며, 다양한 시점의 스냅샷이 그림 8처럼 1초, 4초, 15초 및 24초에서 단일 표적과 다중 표적의 3D 매핑이 잘 나타났다. 애니메이션은 실제 실험 시나리오에 맞게 정렬된 표적 위치를 동적으로 표현한다.
그림 8. | Fig. 8.
두 시나리오 모두에 대한 시간 경과에 따른 표적 추적 결과 | Results of target tracking over time for both scenarios.
Download Original Figure
Ⅴ. 결 론
본 연구는 여러 표적이 있는 시나리오에서 거리-방위 및 거리-고도 평면에서 별도로 식별된 표적을 일치시키는 문제를 효과적으로 해결한다. 3D 위치 추정을 위한 재귀 알고리즘을 사용하여 레이다 데이터 큐브 프레임에서 거리, 방위 및 고도 정보를 반복적으로 추출하였다. 실험 측정을 통해 효과적이고 정밀한 추적을 수행하였음을 검증하였다. 또한 연속적인 전후 이동에 대한 단일 표적과 다수의 표적을 추적하는 데 성공하였다. 향후 연구는 다양한 실내 환경에서 견고성을 향상시키기 위해 알고리즘을 개선하고 송수신 요소의 수를 늘려 레이다 시스템의 각도 분해능을 향상시키는 등의 방향으로 연구가 가능하다.
Acknowledgements
본 연구는 한국전자통신연구원 연구운영지원사업의 일환으로 수행되었음(23ZH1100, 연결의 한계를 극복하는 초연결 입체통신 기술 연구).
References
S. Sun, A. P. Petropulu, and H. V. Poor, "MIMO radar for advanced driver-assistance systems and autonomous driving: Advantages and challenges,"
IEEE Signal Processing Magazine, vol. 37, no. 4, pp. 98-117, Jul. 2020.


S. Kueppers, H. Cetinkaya, and N. Pohl, "A compact 120 GHz SiGe:C based 2×8 FMCW MIMO radar sensor for robot navigation in low visibility environments," in
2017 European Radar Conference(EURAD), Nuremberg, Oct. 2017, pp. 122-125.


T. K. V. Dai, K. Oleksak, T. Kvelashvili, F. Foroughian, C. Bauder, and P. Theilmann, et al., "Enhancement of remote vital sign monitoring detection accuracy using multiple-input multiple-output 77 GHz FMCW radar,"
IEEE Journal of Electromagnetics,
RF and Microwaves in Medicine and Biology, vol. 6, no. 1, pp. 111-122, Mar. 2022.


G. Cai, X. Wang, J. Shi, X. Lan, T. Su, and Y. Guo, "An FMCW MIMO radar-vision fusion algorithm for target classification and localization,"
IEEE Access, vol. 11, pp. 108222-108231, Oct. 2023.


M. J. Lee, M. S. Kang, B. H. Ryu, S. J. Lee, B. G. Lim, and T. B. Oh, et al., "Improved moving target detector using sequential combination of DPCA and ATI,"
The Journal of Engineering, vol. 2019, no. 21, pp. 7834-7837, Sep. 2019.


S. H. Lee, I. O. Choi, M. S. Kang, and K. T. Kim, "Efficient sparse representation algorithm for accurate DOA estimation of multiple targets with single measurement vector,"
Microwave and Optical Technology Letters, vol. 60, no. 1, pp. 31-37, Dec. 2018.


M. S. Kang, K. T. Kim, "Ground moving target imaging based on compressive sensing framework with single-channel SAR,"
IEEE Sensors Journal, vol. 20, no. 3, pp. 1238-1250, Feb. 2020.


M. S. Kang, Y. J. Won, B. G. Lim, and K. T. Kim, "Efficient synthesis of antenna pattern using improved PSO for spaceborne SAR performance and imaging in presence of element failure,"
IEEE Sensors Journal, vol. 18, no. 16, pp. 6576-6587, Aug. 2018.


X. Li, X. Wang, Q. Yang, and S. Fu, "Signal processing for TDM MIMO FMCW millimeter-wave radar sensors,"
IEEE Access, vol. 9, pp. 167959-167971, Dec. 2021.


Y. Su, X. Lan, J. Shi, L. Sun, and X. Wang, "Fast yarget localization in FMCW-MIMO tadar with low SNR and snapshot via multi-DeepNet,"
Remote Sensing, vol. 15, no. 1, p. 66, Dec. 2022.


X. Fang, J. Li, Z. Zhang, and G. Xiao, "FMCW-MIMO radar-based pedestrian trajectory tracking under low-observable environments,"
IEEE Sensors Journal, vol. 22, no. 20, pp. 19675-19687, Oct. 2022.


C. Pfeffer, R. Feger, C. Wagner, and A. Stelzer, "FMCW MIMO radar system for frequency-division multiple TX-beamforming,"
IEEE Transactions on Microwave Theory and Techniques, vol. 61, no. 12, pp. 4262-4274, Dec. 2013.


C. Vasanelli, K. Baur, M. Nezadal, H. Gulan, M. Steiner, and C. Waldschmidt, "Characterization of a mm-Wave automotive radar with a low-RCS MIMO antenna system," in
2018 IEEE Conference on Antenna Measurements & Applications(CAMA), Västerå, Sep. 2018, pp. 1-4.


S. Zainuddin, I. Pasya, N. E. A. Rashid, R. S. A. R. Abdullah, and A. R. Abdullah, "Performance of MIMO FMCW radar in detecting small vessels," in
2018 IEEE International RF and Microwave Conference(RFM), Penang, Dec. 2018, pp. 329-332.


J. K. Park, J. H. Park, and K. T. Kim, "Multipath signal mitigation for indoor localization based on MIMO FMCW radar system,"
IEEE Internet of Things Journal, vol. 11, no. 2, pp. 2618-2629, Jan. 2024.


R. Feng, E. D. Greef, M. Rykunov, H. Sahli, S. Pollin, and A. Bourdoux, "Multipath ghost recognition for indoor MIMO radar,"
IEEE Transactions on Geoscience and Remote Sensing, vol. 60, pp. 1-10, 2021.


R. Amar, M. Alaee-Kerahroodi, and M. R. Bhavani Shankar, "FMCW-FMCW interference analysis in mm-wave radars: An indoor case study and validation by measurements," in
2021 21st International Radar Symposium(IRS), Berlin, Jun. 2021, pp. 1-11.


S. Rao, A. V. Mani, "Interference characterization in FMCW radars," in
2020 IEEE Radar Conference (RadarConf20), Florence, Sep. 2020, pp. 1-6.


S. Jin, S. Roy, "FMCW radar network: Multiple access and interference mitigation,"
IEEE Journal of Selected Topics in Signal Processing, vol. 15, no. 4, pp. 968-979, Jun. 2021.


A. Haderer, P. Scherz, C. Pfeffer, and A. Stelzer, "Real-time implementation of an imaging algorithm for FMCW MIMO radar systems," in
2012 9th European Radar Conference, Amsterdam, Oct.-Nov. 2012, pp. 186-189.

N. Knudde, B. Vandersmissen, K. Parashar, I. Couckuyt, A. Jalalvand, and A. Bourdoux, et al., "Indoor tracking of multiple persons with a 77 GHz MIMO FMCW radar," in
2017 European Radar Conference(EURAD), Nuremberg, Oct. 2017, pp. 61-64.


F. Liang, F. Qi, Q. An, H. Lv, F. Chen, and Z. Li, et al., "Detection of multiple stationary humans using UWB MIMO radar,"
Sensors, vol. 16, no. 11, p. 1922, Nov. 2016.




J. Yang, J. Thompson, X. Huang, T. Jin, and Z. Zhou, "FMCW radar near field three-dimensional imaging," in
2012 IEEE International Conference on Communications (ICC), Ottawa, ON, Jun. 2012, pp. 6353-6356.



J. M. Lopez-Sanchez, J. Fortuny-Guasch, "3-D radar imaging using range migration techniques,"
IEEE Transactions on Antennas and Propagation, vol. 48, no. 5, pp. 728-737, May 2000.


A. Ganis, E. M. Navarro, B. Schoenlinner, U. Prechtel, A. Meusling, and C. Heller, et al., "A portable 3-D imaging FMCW MIMO radar demonstrator with a 24×24 antenna array for medium-range applications,"
IEEE Transactions on Geoscience and Remote Sensing, vol. 56. no. 1, pp. 298-312, Jan. 2018.


J. Jung, S. Lim, S. C. Kim, and S. Lee, "Solving Doppler-angle ambiguity of BPSK-MIMO FMCW radar system,"
IEEE Access, vol. 9, pp. 120347-120357, Aug. 2021.


M. M. G. Yowel, D. H. Oh, H. J. Kim, B. J. Jeong, and J. H. Han, "SNR improvement for heart rate estimation using mmWave 79 GHz FMCW MIMO radar," in
2023 International Symposium on Electromagnetic Compatibility-EMC Europe, Krakow, Poland, Sep. 2023, pp. 1-5.