I. 서 론
우주감시레이다는 수백 km~천 km 이상의 거리에서 약 7,800 m/s로 빠르게 이동하는 위성을 탐지하는 초장거리 레이다로써, 고출력의 대형 안테나를 필요로 한다. 대형 안테나는 좁은 빔폭을 가지고 있고 따라서 좁은 빔폭으로 넓은 영역을 탐색하는 것에는 한계가 있으므로, 과거에는 알고 있는 있는 위성의 위치를 지정받아서 추적하는 것이 일반적이었다. 대표적인 우주감시 추적 레이다로는 ALTAIR, TRACDECX, ALCOR등이 있다[1]. 그러나 자유롭게 빔조향이 가능한 능동위상배열 레이다 및 디지털 레이다 개발이 활발히 이루어지면서 우주감시레이다도 탐색 기능이 추가되었고 대표적으로 미국의 Space Fence[2],[3], 독일 GESTRA[4], 일본의 Kamisaibara[5] 등이 개발되어 운용되고 있다. 현재 개발된 우주감시레이다 중 가장 큰 규모로는 Lockheed Martin의 Space Fence가 개발되었으며 출력 1 MW 이상, 배열 개수는 송신 3만 개 이상, 수신 8만 개 이상의 대형 안테나가 설치되어 있다. 대형 안테나의 사용에 따른 전력 및 좁은 빔폭으로 인해 탐색 시간이 증가되므로 고출력의 대형 안테나를 운용하기 위해서는 탐지 영역에 따라서 파형이나 빔운용을 다르게 적용하여야 시간 및 출력 자원을 효율적으로 사용할 수 있다.
우주감시레이다는 지상에서의 표적을 탐지하는 레이다와는 대상 표적의 위치 및 이동 특성이 다르므로 표적 특성을 먼저 파악하고 빔 운용 방안을 설계하여야 할 것이다. 본 논문에서는 우주감시레이다의 탐색 빔그리드 설정 방안을 제시하기 위해서 다음과 같이 구성하였다.
II장에서는 위성 궤도 특징, 안테나 설계안 등 우주감시레이다의 개요에 대해서 설명하였고, III장에서는 탐색 빔그리드를 설계하기 위한 빔확장 방안, 탐색 빔그리드 설정 알고리즘, 그리고 설계된 빔그리드를 적용한 레이다 시뮬레이션 결과를 비교 분석하여 나타내었으며, 마지막으로 IV장에 결론으로 기술하였다.
II. 우주감시레이다 개요
우주감시레이다를 개발하기 위해서는 먼저 탐지 대상 표적의 특성을 파악하여야 한다. 탐지 대상 표적인 위성은 지구 주위를 궤도 운행하며, 궤도 특징은 크게 이심률, 고도, 궤도 경사의 세 가지 기준으로 분류할 수 있다.
이심률은 위성 궤도가 원에서 얼마나 벗어나 있는지를 수치화한 값이며 0에 가까울수록 원형 궤도를 나타내고, 값이 커질수록 타원으로 운행함을 의미한다. 고도는 지구 표면으로부터의 거리를 나타내고, 궤도 경사는 적도를 기준으로 기울어진 정도를 나타낸다.
위성의 데이터는 UCS(Unions of Concerned Scientists)에 공유된 것을 사용하였으며 분류결과는 다음과 같다.
그림 1은 이심률에 따른 위성 개수를 나타낸 것이며, 이심률 0.14 이하를 원형궤도로 정의할 때 전체 7,503개 중 7,445로 거의 대부분의 위성이 원형궤도로 운행한다.
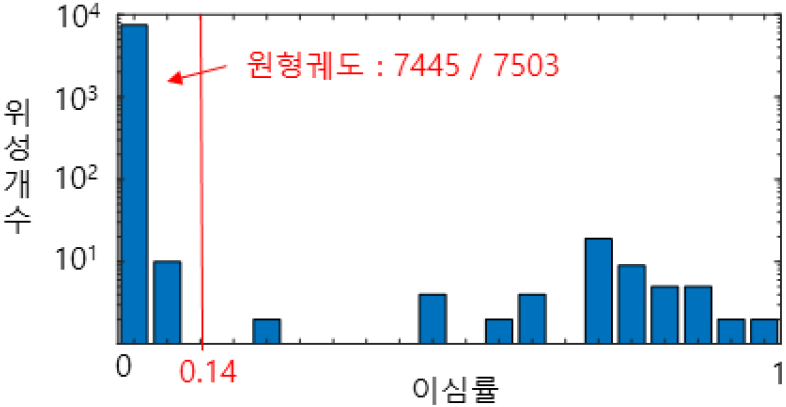
고도 별 분포는 저궤도(LEO: 200~200 km), 중궤도(MEO: 2,000~34,000 km), 고궤도(HEO: 34,000 km~)로 나누어지는데 원형궤도를 운행하는 7,445개 중 약 90 % 이상인 6,742개가 저궤도에 분포되어 있다(표 1).
| 분류 | 원형궤도 (이심률 < 0.14) | 타원궤도 | ||
| 저궤도 | 중궤도 | 고궤도 | (이심률>0.14) | |
| 개수 | 6,742 | 144 | 559 | 58 |
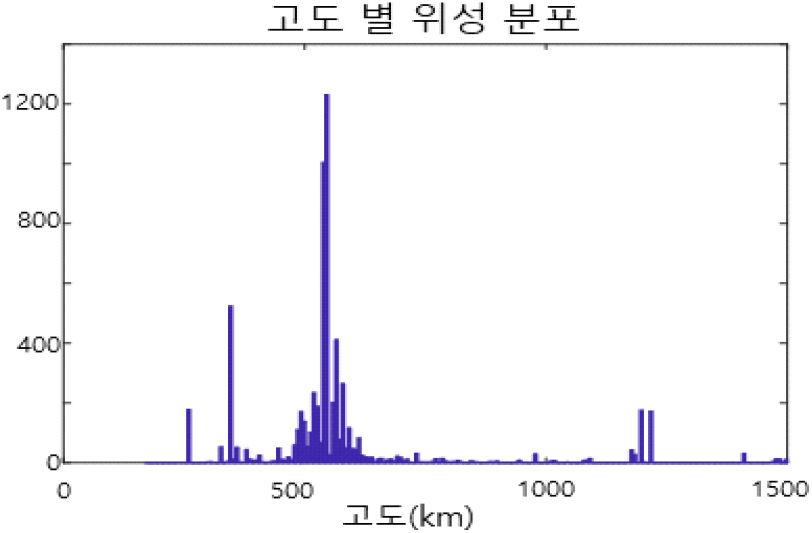
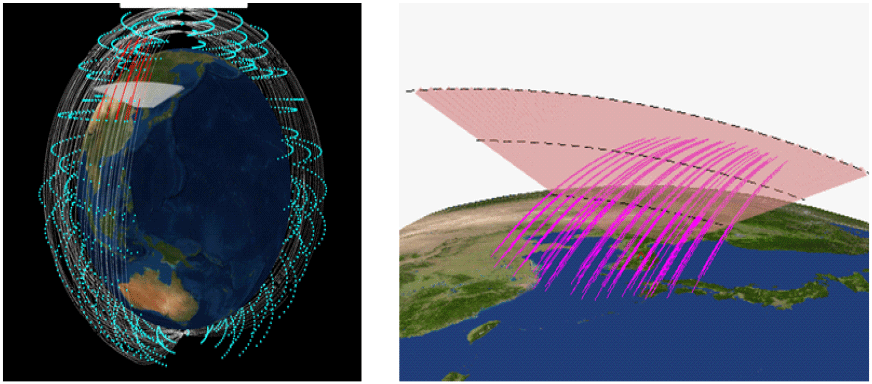
저궤도 위성을 다시 고도별로 분포를 보면 다음 그림 2 및 그림 3에서와 같이 나타내어진다. 그림 2에서는 레이다가 탐색을 위해서 방위각 ±60°로 탐색펜스를 설정(초록색) 후 일정 시간 관측하였을 때 탐색펜스를 통과하는 위성을 나타낸 것이고, 그림 3에서는 저궤도 위성의 고도 별 분포를 나타내었으며 대부분이 고도 700 km 이하에 분포함을 알 수 있다.
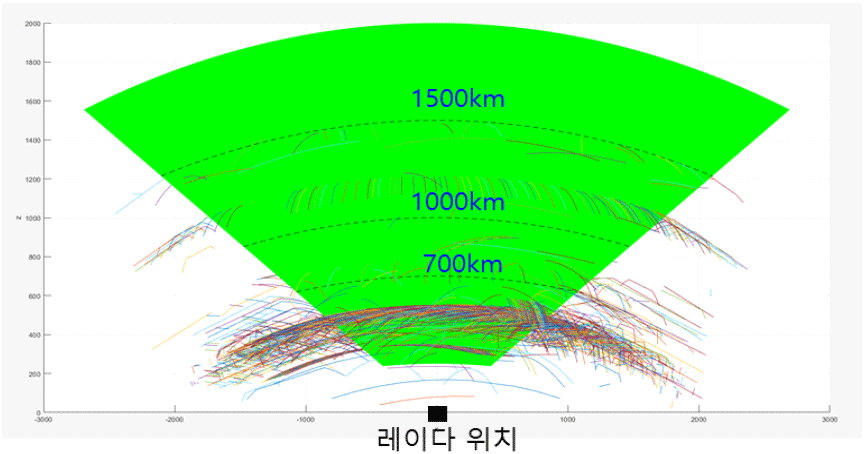
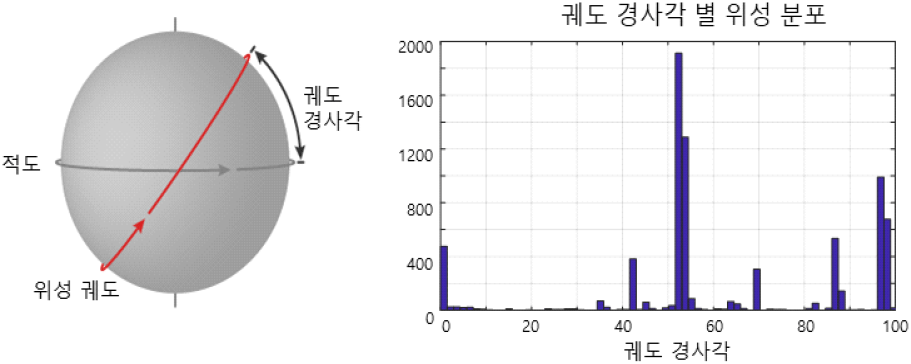
그림 4에서 좌측 그림은 궤도 경사를 설명하는 것이고 우측 그림은 궤도 경사 분포를 나타낸 것이다. 궤도 경사는 적도 근처는 0도, 90도에 가까우면 극궤도인데, 참고로 한 자료에서의 위성은 극궤도와 50~60도 사이에 많이 분포해있다. 관측지를 위도 37도로 설정하면 적도궤도는 거의 관측이 어렵지만, 경사궤도와 극궤도는 지구 자전과 궤도 운행 시점이 맞으면 하루에 한번 또는 두 번 이상 관측 가능하다.
이상으로 탐지 목적 대상인 위성 궤도별 특징을 고려하면, 대부분의 위성은 원형 궤도를 운행하고, 고도별 특징으로는 저궤도에 위치하며 그 중에서도 고도 500~700 km 사이에 많이 분포한다. 물론 UCS 데이터에 포함되지 않은 수많은 소형 위성들도 300 km 이하의 낮은 고도에 위치하고 있다. 위성을 탐지하기 위한 우주감시레이다를 설계한다면, 무조건 최장거리 탐지가 가능한 것을 선택하는 것이 아니라 확률적으로 많은 위성이 탐지 가능한 범위에서 설계되어야 하며 특히 빔조향 손실을 고려하면 자원을 효율적으로 사용하기 위해서 빔 조향 별 빔 운용과 파형을 다르게 적용해야 하는데 다음 절에 그 과정을 나타내었다.
본 절에서는 우주감시레이다의 체계설계를 위해서 탐색 영역을 설정한 후 탐색 범위 안에서 최장거리 탐지가 가능한 안테나 사양을 설계하고 확률적으로 많은 위성을 탐지할 수 있는 범위로 안테나 형상을 설정하는 과정을 기술한다.
먼저 탐색 영역을 소형 위성 기준(RCS: radar cross section 0.01 m2)으로 레이다 빔조향이 가능한 범위에서 고도 500 km, 1,000 km, 1,500 km까지 탐지 가능한 안테나 사양을 설계하였다. 본 논문에서는 안테나 형상의 크기에 따라 빔폭, 프레임타임 등 비례적으로 달라질 수 있는 부분을 설명하기 위함이므로, 구체적인 숫자는 요구사항과 시스템 설정 방법에 따라 달라질 수 있다. 그림 5에서는 각 탐색 영역 설정에 따른 설계된 안테나 형상과, 빔폭, 탐색 범위, 그리고 프레임타임을 순서대로 나타내었다. 우주감시레이다와 같이 초장거리 탐지를 위해서는 송수신 일체형을 사용하는 것보다 잡음지수, 방열, 설치 효율성 등을 고려하여 송수신 분리형을 사용하는 것이 효율적인데, 수신 안테나 형상도 송신 안테나 형상에 비례하여 커지므로 아래 그림에서는 송신 안테나에 대한 사양만을 나타내었다.
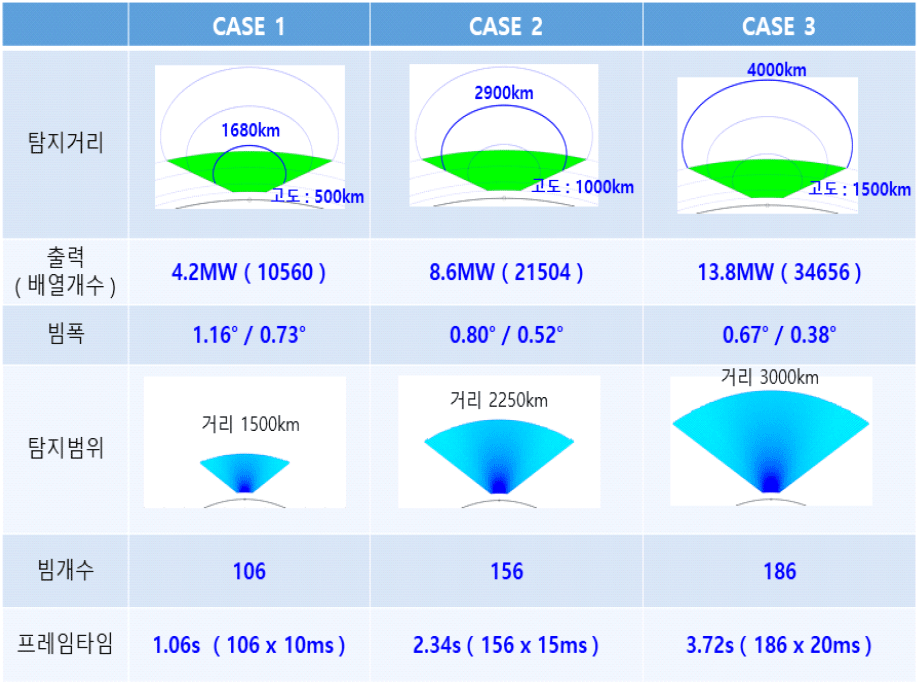
먼저 그림 5에서 Case 1은 탐색 영역을 고도 500 km로 설정한 것이며, 레이다 빔조향을 ±60°로 하면 동일한 고도를 유지하는 양 끝에서의 거리는 약 910 km이다. 그러나 빔조향각(θ)에 따른 손실(BS LOSS)과 이를 고려한 빔조향 0도에서의 탐지거리(R0)는 식 (1) 및 식 (2)에서 구할 수 있다.
빔조향각 60도에서의 빔조향 손실은 약 9 dB이고 거리 Rθ는 910 km이므로 이를 수식에 대입하면 빔조향 0도에서의 탐지거리(R0)는 1,529 km 이상이어야 한다. 따라서 그 이상을 탐지 가능한 안테나를 설계한 결과 송신 배열 10,500개, 출력 4.2 MW로 설계하였으며, 이때 안테나 빔폭은 방위각 1.16도이므로 이를 기준으로 탐색영역 120도의 범위에 106개의 빔이 할당된다. 전파는 빛의 속도로 왕복하므로 최소 1,500 km 이상 관측하기 위해서는 최소 10 ms 이상이 필요하므로 각 빔 당 동일하게 10 ms를 할당하면 총 106개의 빔을 탐색하는 시간은 1.06초(10 ms×106개)가 된다. Case 2, 3도 고도 1,000 km, 1,500 km로 설정 후 같은 과정으로 안테나 형상과 빔폭, 프레임타임 등을 구한 것이다.
안테나 크기와 출력을 크게 할수록 먼 거리 탐지가 가능하지만, 빔폭 감소와 그에 따른 프레임 타임 증가, 그리고 설치 및 운용 비용 등을 고려할 때, 확률적으로 많은 위성을 탐지할 수 있는 탐지범위로 제한하여 설정하는 것이 필요하다. 대부분의 저궤도 위성은 2-1절에서 살펴본 바와 같이 고도 1,500 km 이하에서 특히 고도 700 km 근처에 많이 분포하고, 연구용으로 사용하는 소형 큐브는 500 km 이하에 대부분 위치할 것으로 가정하였다. 본 연구에서는 소형 큐브에 해당되는 RCS 0.01 m2인 물체는 고도 500 km까지는 빔조향 60도까지 탐지 가능하고 그보다 큰 물체는 더 먼 거리도 탐지 가능하도록 Case 1을 선택하였다.
<설계된 안테나 사양>
안테나 출력: 4.2 MW, 이득: 44.26 dB
안테나 빔폭: 방위각 1.16°/고각 0.73°
빔그리드 개수: 106개(프레임 타임 1.06 s)
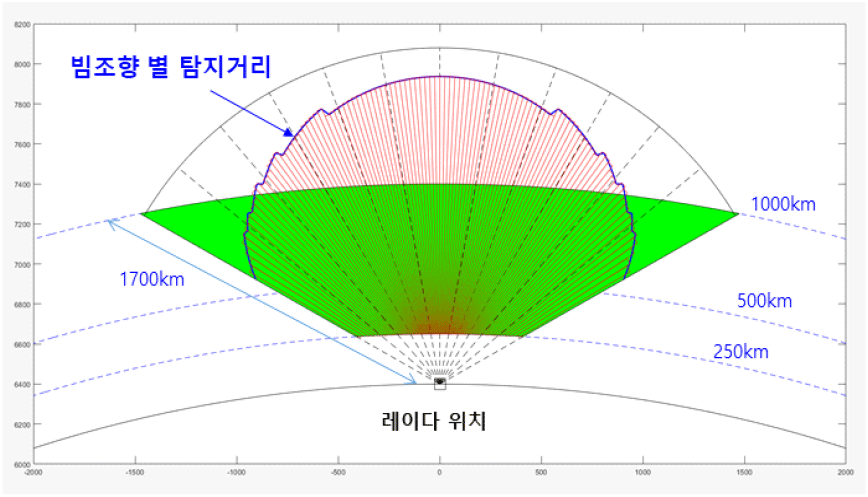
선택된 안테나 사양에서 RCS 0.01m2 기준으로 탐지 가능한 범위는 다음의 그림에 나타내었으며, 고도 500 km까지는 모든 빔조향 각도에서 탐지 가능하지만 고도 500 km 이상에서는 제한된 범위에서의 탐지가 가능하다. 그러나 일반 위성과 같이 RCS가 그보다 클 경우에는 전 영역에서도 탐지 가능하다(그림 6).
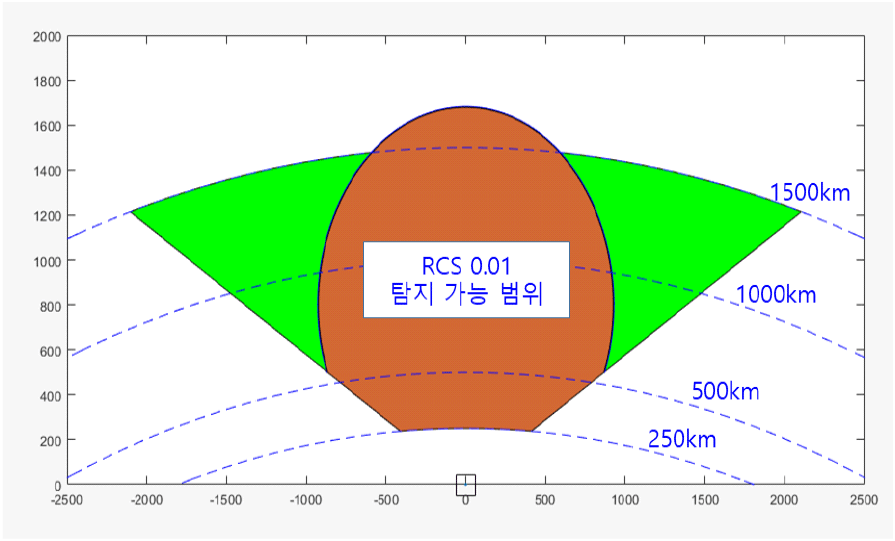
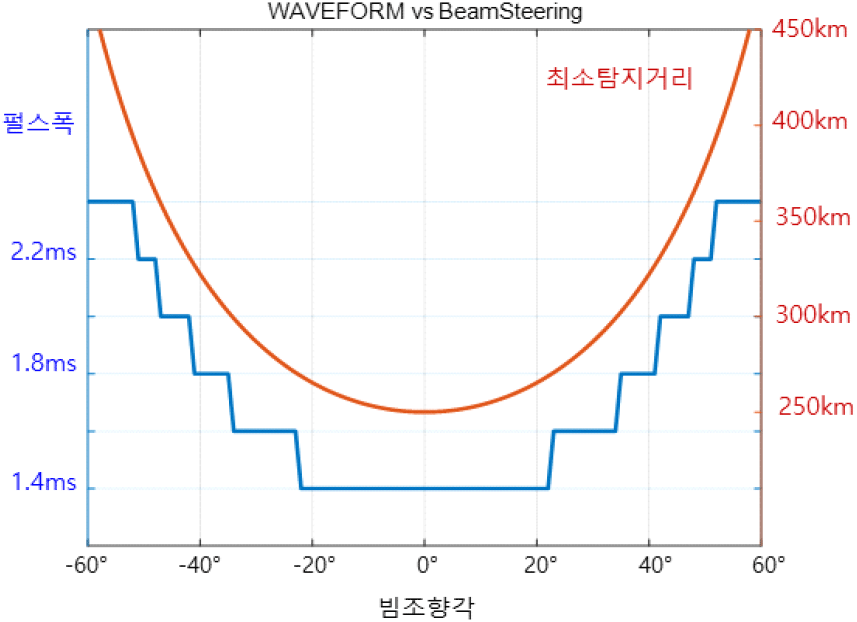
지구 주위를 공전하는 위성이 궤도를 형성하기 위해서는 고도 별 궤도를 유지할 수 있는 속도가 필요하며 고도가 낮아질수록 더 빠른 속도를 필요로 한다. 고도 250 km 이하에서는 궤도를 유지하기 위해서는 빠른 속도가 필요하며 그에 따라 물체가 연소될 수 있으므로, 실제 대부분의 위성은 고도 250 km 이상에 분포되어 있다. 따라서 우주감시레이다는 고도 250 km부터 탐지 가능하도록 설정하면 각 빔조향각 별 최대 펄스폭이 계산된다. 빔조향각이 0도일 경우, 최소 탐지거리는 250 km 이상이며 이에 해당되는 시간은 1.66 ms이므로 펄스폭은 이보다 작아야 한다. 마찬가지로 다른 빔조향각에 대해서도 고도 250 km에 해당되는 거리를 계산하여 그보다 작은 시간으로 펄스폭을 할당하며 이를 단계 별로 나타낸 결과를 그림 7에 나타내었다.
각 빔조향각(θ) 별로 최소 탐지거리를 고려한 최대 펄스폭(τ(θ))이 할당되면, 레이다 방정식을 사용하여 빔조향 손실과 펄스폭 에 따른 적분을 고려한 탐지 가능 거리를 식 (3)과 같이 계산할 수 있다.
where, Pt: 송신 출력
τ(θ): 빔조향각에 따른 펄스폭
Gt/Gr: 안테나이득 (송신/수신)
λ: 파장길이
k: 볼츠만상수 1.38e-23
T: 절대온도 290 K
F: 잡음지수
Loss: 손실
앞의 식 (3)을 적용하여 펄스폭 2 ms 사용 시 Boresight에서 최대 1,680 km를 탐지할 수 있는 안테나 사양을 적용하면 빔폭은 1.16°이고, 이를 기준으로 기본 탐색 빔그리드를 설정하면, 빔조향 별 최대 펄스폭을 적용한 탐지거리 성능은 식 (4)와 같이 펄스폭 및 빔조향 손실에 의해 비례적으로 구할 수 있다.
빔조향 별 다른 펄스폭의 파형을 적용하여 탐지거리를 구하면 그림 8과 같이 나타내어진다.
III. 탐색 빔그리드 설정 방안
대부분의 저궤도 위성은 고도 1,000 km 이내에 위치하므로 고도 1,000 km 이상까지 RCS 0.01 m2의 물체를 탐지할 수 있도록 파형을 설정하는 것은 비효율적인 자원 분배이다. 따라서 탐지성능이 기대치 이상으로 넘어선 빔조향각에서는 이득을 낮추는 대신 송신빔을 확장시켜서 한 번에 더 넓은 공간을 탐색할 수 있도록 하는 것이 효율적이다.
본 장에서는 먼저 3-1절에서 송신 빔 확장 방안에 대해서 설명한 후, 3-2절에서는 우주감시레이다의 특성에 맞게 각 빔조향각 별로 빔 형상과 파형을 결정하는 빔그리드 최적화 방안에 대해서 소개하고, 3-3절에서는 빔그리드 최적화를 하지 않고 전부 펜슬빔으로 송신한 경우와 탐색 빔그리드를 최적화한 경우에 대해서 우주감시레이다 탐색을 모의한 시뮬레이션 결과를 나타내어 비교하였다.
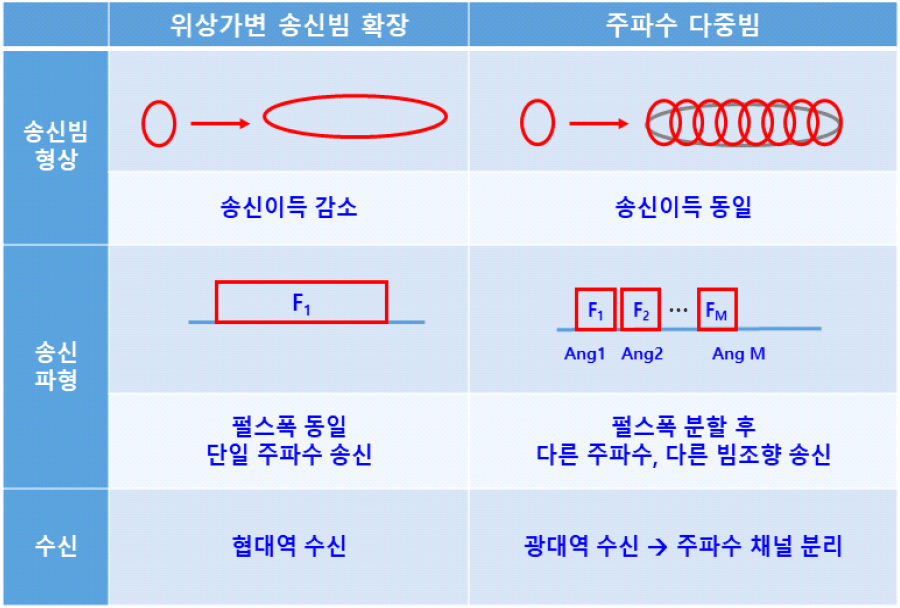
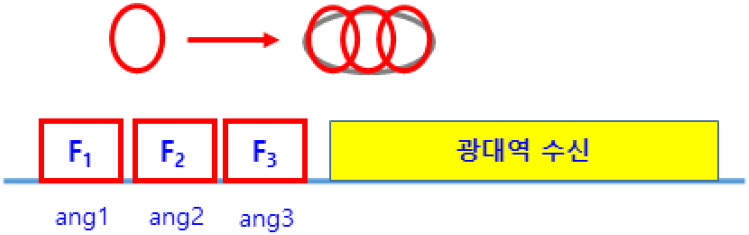
이득을 낮추고 송신빔을 확장시키는 방법으로 본 연구에서는 위상가변 송신빔 확장/주파수 다중빔 방식을 적용하였으며, 그림 9에 각 방식에 대한 특성을 정리하였다.
위상가변 송신빔 확장 방법은 송신 안테나 배열의 위상을 가변시켜서 빔폭을 확장하며 확장된 빔폭만큼 이득이 감소한다. 파형은 펜슬빔에서와 동일한 파형을 사용하며 단일 주파수 송신, 협대역 수신을 적용한다. 다중주파수 방법은 펜슬빔을 사용했을 경우에 사용되는 송신 파형을 분할하여 각 분할된 파형에 다른 주파수, 다른 빔조향을 적용하여 간섭이 발생하지 않도록 한다. 수신은 광대역으로 수신하여 한 번에 다른 방향으로 송신한 신호를 수신할 수 있으며 각 주파수 별 채널 분리를 통해 동시에 송신한 빔조향각 별 신호처리를 따로 한다.
빔을 확장하는 방법에 대해서는 크기 또는 위상을 변화시킴으로써 확장시킬 수 있으며, 각 방안에 대한 방법 및 성능 비교 결과도 이미 분석되어 있다[6]. 그러나 송신 안테나의 경우 출력을 최대로 송신하도록 증폭기가 설계되어 있으므로 크기 변화를 통한 빔확장은 송신빔에는 적합하지 않고, 위상 가변으로 빔을 확장하는 방식을 적용하였으며[7], 원하는 영역을 설정하고 해당 영역에 빔패턴이 들어오도록 위상분포를 찾는 방법을 적용하였다.
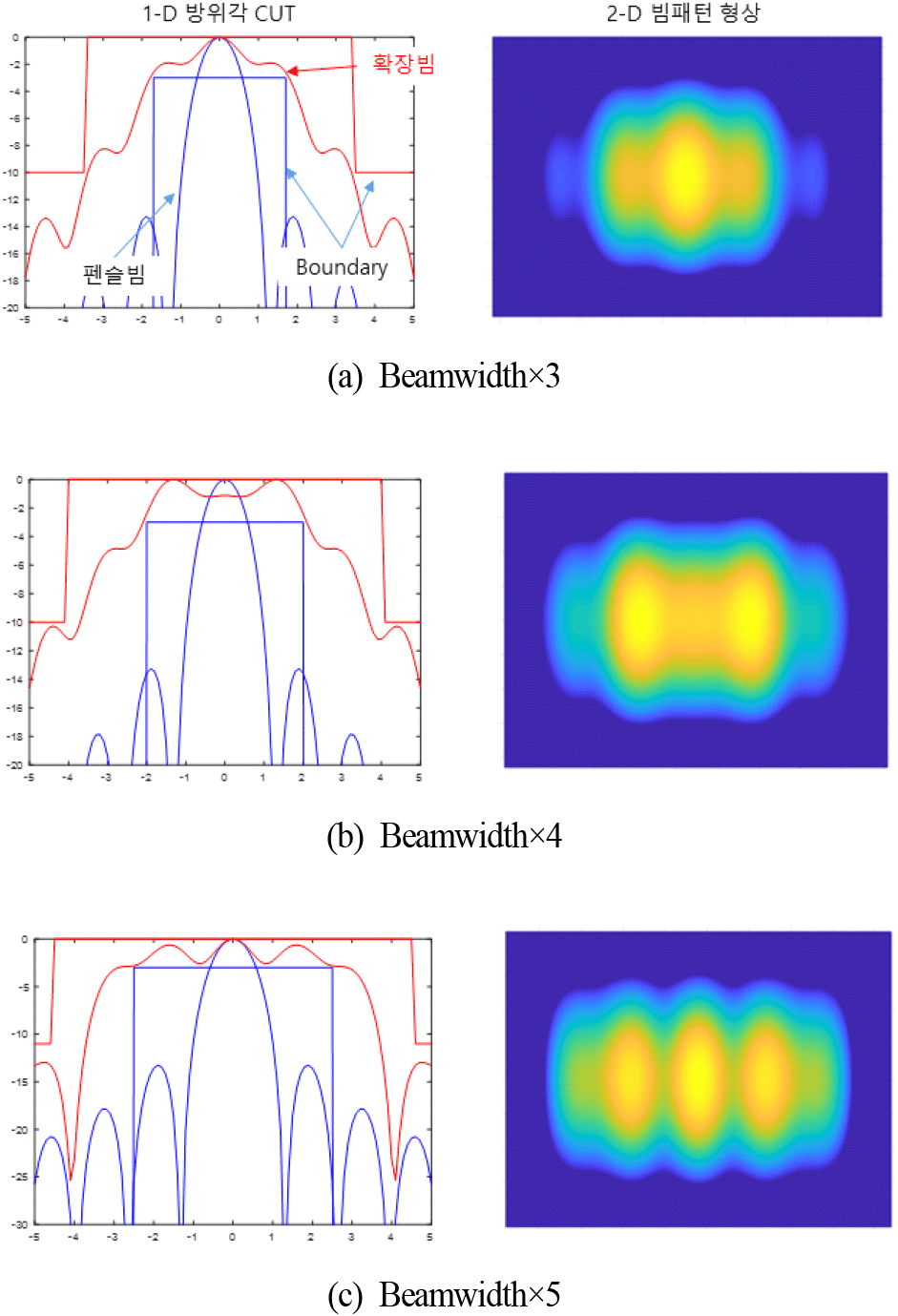
위상분포를 가변하여 빔을 확장하는 방식은 송신 펄스 폭은 그대로 유지한 채 빔이 방사되는 송신 범위를 넓히고 수신 다중빔 개수를 늘려서 탐색하는 방식이다. 송신 확장빔은 이득이 5 dB 이상 마진이 있을 때에는 적용 가능하지만 그 이하에서는 오히려 확장빔을 원하는 형태로 최적화하기가 어려워지며 그에 따른 손실도 크게 된다. 위상가변을 통한 송신빔 확장은 다항계수를 사용한 위상분포로 최적화하였고 각 빔폭 별 송신빔 형상은 그림 10과 같다.
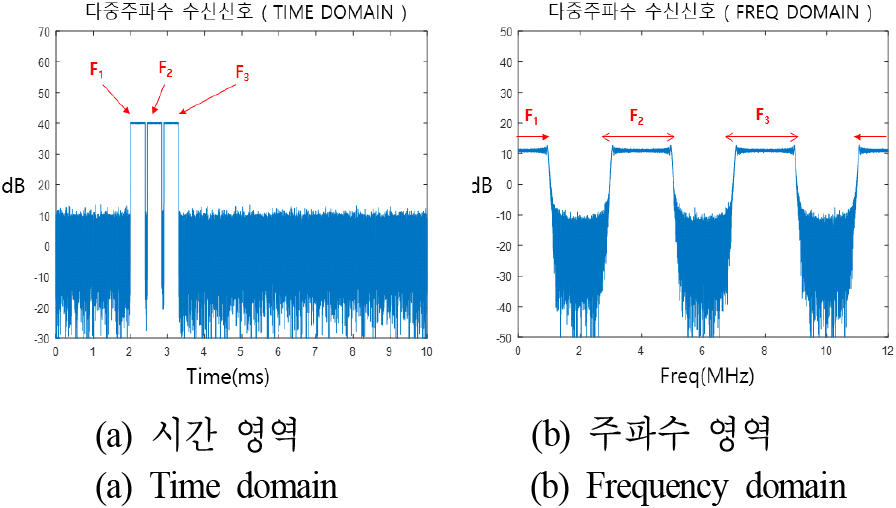
송신 펄스폭을 나누어서 각각 다른 주파수로 다른 방향으로 송신하고, 광대역으로 한 번에 수신하여 주파수 채널 별 분석을 통해 탐색하는 방식이다. 이득 마진이 높을 때에는 더 많은 개수로 송신펄스를 나누어서 적용하겠지만 이는 수신 대역폭이 넓어져야 하고 처리해야 하는 수신빔 채널 개수도 각 주파수 채널 별로 모노펄스를 고려하면 더욱 많이 증가된다. 이득 마진이 충분하지 않아서 위상가변 송신빔 확장 손실이 클 때 대신 사용할 수 있는 방식이다. 그림 11은 3배 확장한 주파수 다중빔 적용 시 광대역으로 한번에 수신되는 신호를 모의하였으며, 그림 12(a)는 시간영역에서의 신호 크기, 그림 12(b)는 주파수 스펙트럼을 나타내었다.
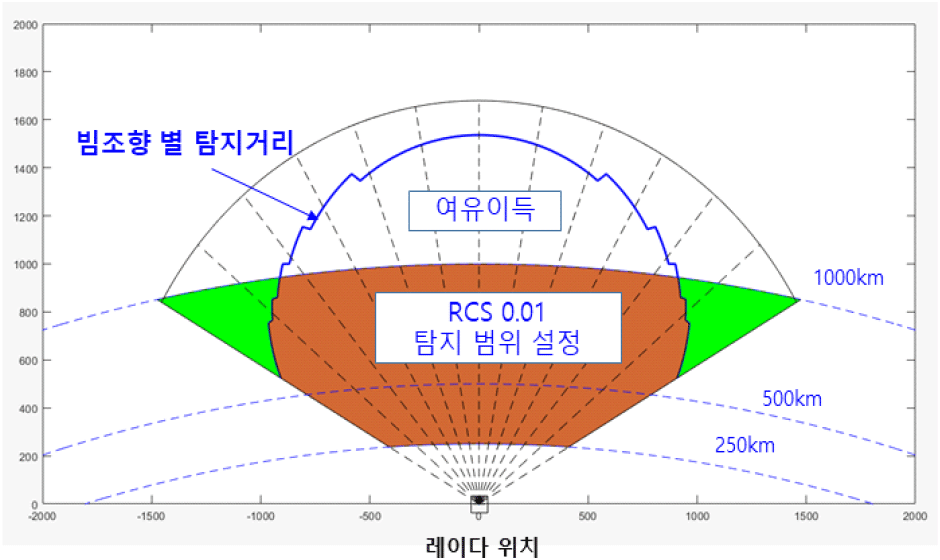
우주감시레이다가 저궤도 위성 탐지를 목표로 한다면 먼저 탐색 영역을 설정하여야 한다. 2-1절에서 언급한 바와 같이 저궤도에서 공개적으로 알려진 대부분의 위성의 대부분이 고도 1,000 km 이하 특히 700 km 부근에 있고, 소형 위성은 그보다 더 낮은 고도에 분포한다. 그러나 알려져 있지 않은 물체나 파편 등을 탐지하기 위해서 소형 표적(RCS 0.01m2)에 대해서는 고도 1,000 km 이하까지 탐지하는 것을 목표로 하면 탐지 범위는 다음과 같이 설정할 수 있다. 그림 8에 나타낸 탐지거리 성능으로부터 고도 1,000 km 이하까지는 소형 표적이 탐지 가능한 범위로 설정하고 이보다 큰 표적은 그 이상으로 탐지할 수 있도록 탐색 범위를 설정할 수 있다. 이 때 RCS 0.01 m2의 표적을 탐지할 수 있는 성능이 고도 1,000 km를 초과하는 부분은 이득의 마진이 있는 것으로 보고 이를 여유이득으로 설정할 수 있다. 설계된 안테나 사양에서의 탐지가능범위와 설정된 탐지범위 사이에 남는 이득을 여유이득이라 하면, 여유이득만큼 송신빔을 확장할 수 있다(그림 13).
각 빔조향각 별 빔 형상을 결정하는 방법은 다음과 같다. 앞서 빔조향 손실과 최대 펄스폭을 고려하여 빔조향각별로 이득의 마진, 즉 여유이득이 5 dB 이상일 경우는 송신 확장빔, 3~5 dB는 다중주파수 빔, 3 dB 이하는 펜슬빔 사용으로 설정하였다. 그림 14는 빔조향각 별 여유 이득 및 그에 따른 빔 확장 설정 방안을 나타낸 것이며, 빔을 확장시키면서 확장빔에 따른 손실 또는 또는 다중주파수 적용 시 펄스폭 감소에 따른 손실도 함께 나타내었다.
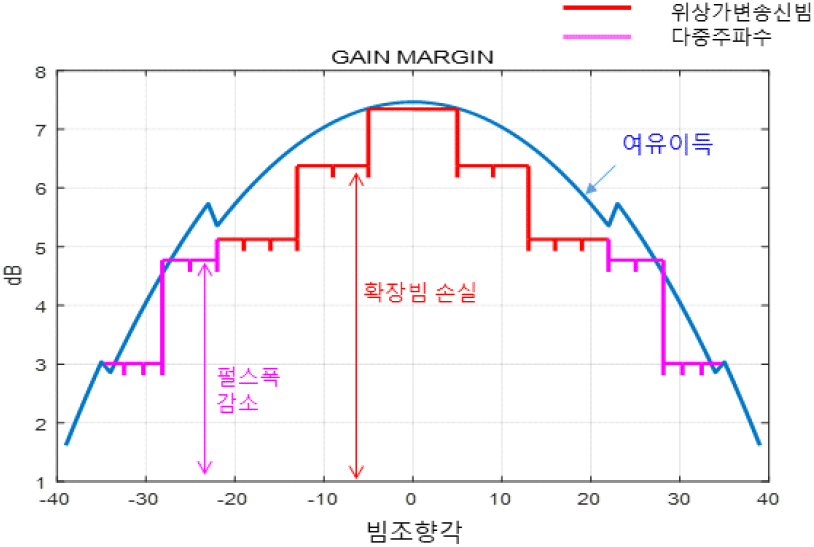
예를 들어 빔조향각 −30도에서는 여유이득이 3 dB 이상이고 이 때에는 다중주파수를 적용하여 2개의 서로 다른 빔을 송신하도록 한다. 2개의 빔으로 분할하였으므로 송신 펄스 폭을 작게 하여 그에 따른 손실은 약 3 dB로 나타내어진다. 빔조향각 −10도에서는 여유이득이 6 dB 이상으로 송신빔 확장을 통해 기존 빔폭의 3~4배 사이로 빔을 확장하여 송신하며, 빔을 확장한 만큼 송신이득 감소로 나타낼 수 있다.
확장빔 설정 과정은 다음과 같이 구한다. 펜슬빔으로 적용하였을 경우 전체 빔 개수를 Nbeam이라고 하면, 펜슬빔으로 적용한 빔그리드를 기준으로 빔의 개수를 늘리면서 확장하는 방식을 적용하였고, 각 빔그리드 위치에서 여유이득 값에 따라 빔 방식을 선택하고, 빔확장에 따른 이득 손실이 여유이득(gain margin)에 가까운 값이 되도록 빔을 확장해 나가면서 새로운 빔그리드를 형성하도록 하였다. 예를 들어 각 방식에 따라 M배만큼 확장시켰다면, 다음번 빔 순서는 n + M에서 다시 이 과정을 반복함으로써 전체 탐지 영역을 커버하도록 한다.
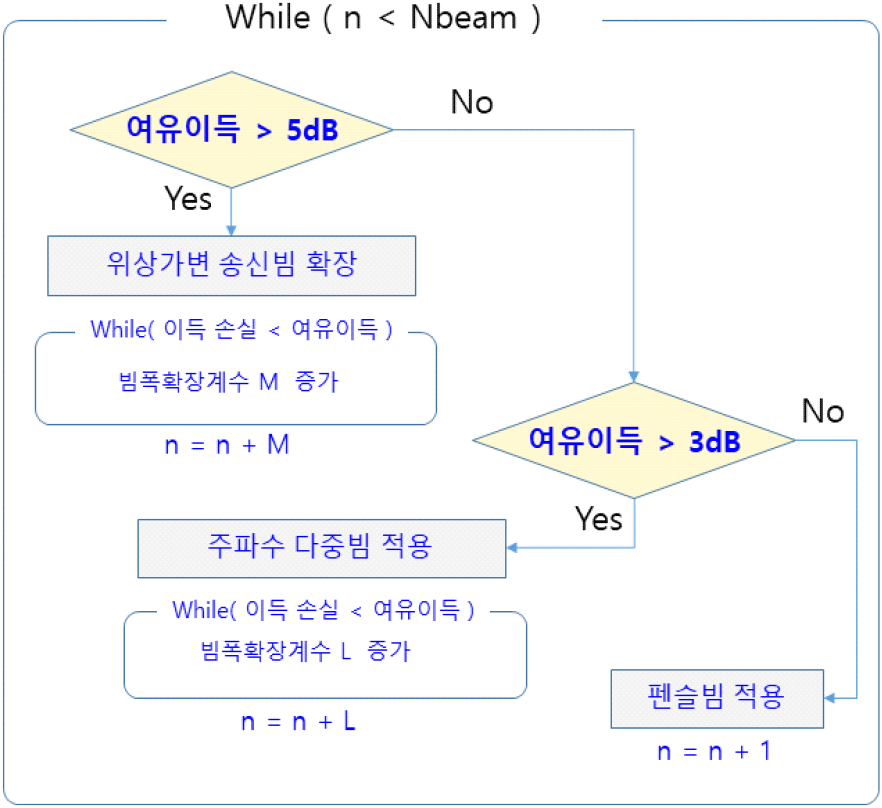
이러한 빔 설정 과정을 다음 그림에 순서도로 나타내었다. 빔그리드 최적화를 하지 않고 전부 펜슬빔으로 구성할 경우 빔 개수를 Nbeam이라고 하면, 펜슬빔으로 적용한 빔그리드를 기준으로 빔의 개수를 늘리면서 확장하는 방식을 적용하였다(그림 15).
순서도에서 먼저 가장 여유이득이 높은 Boresight부터 시작한다. 순서도에 따라서 해당 빔 위치에서의 여유이득을 비교하며, 여유이득이 5 dB보다 높으면 위상가변 송신빔 확장을 선택한다. 이 때 빔폭확장계수 M은 빔폭의 몇 배만큼 확장시키는지를 의미하며 기본 빔폭의 M배만큼 확장시켰을 때의 이득 손실이 여유이득에 가까워질때까지 확장시킨다. M이 결정되면 기본 빔그리드에서 빔 번호 n을 M만큼 증가시킨 후 다시 여유이득에 따라서 다음 번 빔 확장 방안을 결정한다. 여유이득이 5 dB보다 낮고 3 dB보다 높을 경우에는 주파수 다중빔을 선택하며, 빔폭확장계수 L을 2부터 증가시키면서 여유이득에 가까워질때까지 찾는다. L이 결정되면 다시 빔번호를 L만큼 증가시키고 다음 빔으로 넘어가며, 이 과정을 반복함으로써 전체 탐지 영역을 커버하도록 한다.
이 과정은 기본 빔그리드를 기본으로 하기 때문에 최적화를 매우 간단하게 찾을 수 있다. 이와 같은 방식으로 새로운 빔그리드를 형성하면 그림 16에서와 같이 나타내어진다.
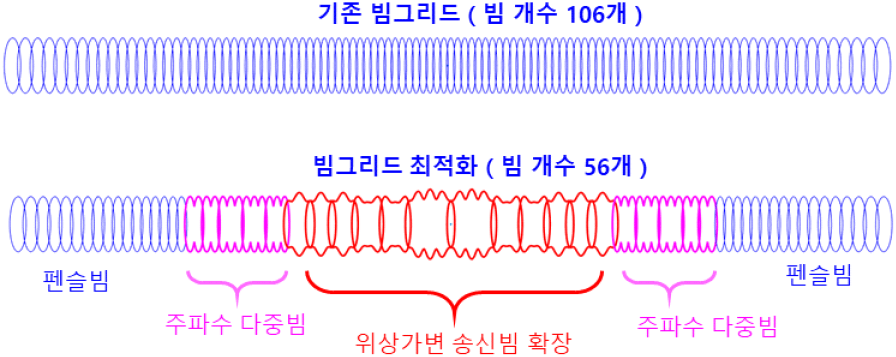
그림 17에서 파란색 실선은 빔확장하지 않았을 경우의 탐지거리이고, 고도 1,000 km까지 표현된 부분은 빔 확장 시의 탐지거리를 의미한다.
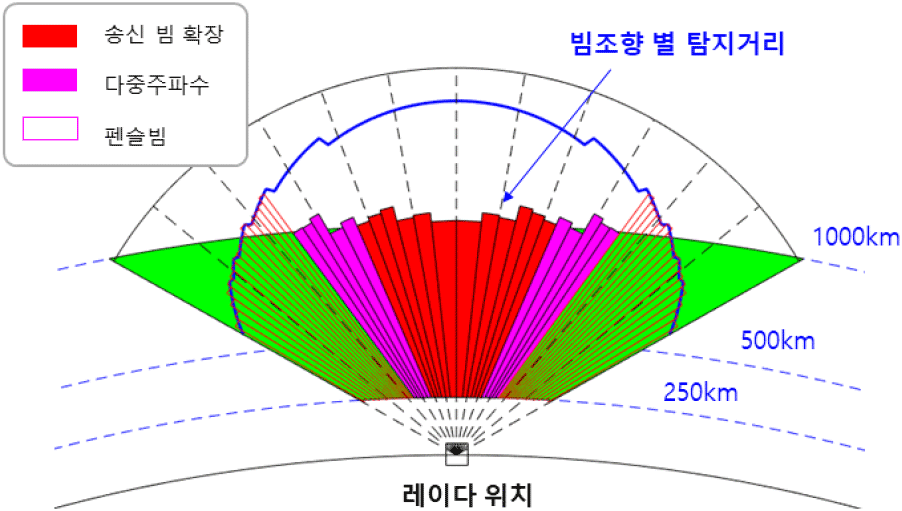
앞서 설명한 방식으로 빔조향각 별로 여유 이득에 따른 빔확장 방식을 사용하여 빔그리드 최적화 결과 빔의 총 개수는 56개이며, 전부 펜슬빔으로 설정했을 경우 총 106개에 비해서 탐색시간을 거의 반으로 줄일 수 있다.
본 절에서는 빔그리드 형상에 따른 레이다의 탐지 성능을 시뮬레이션을 통해 비교 분석하였다. 실제 위성은 고도 별로 일정하게 분포되어 있지 않으므로 시뮬레이션을 위해서 고도 별로 균일하게 위성이 분포된 상황을 모의하였다. 그림 18에서 검은 색 점들은 고도 1,500 km까지 고도 별로 일정하게 분포된 위성의 위치를 나타낸다.
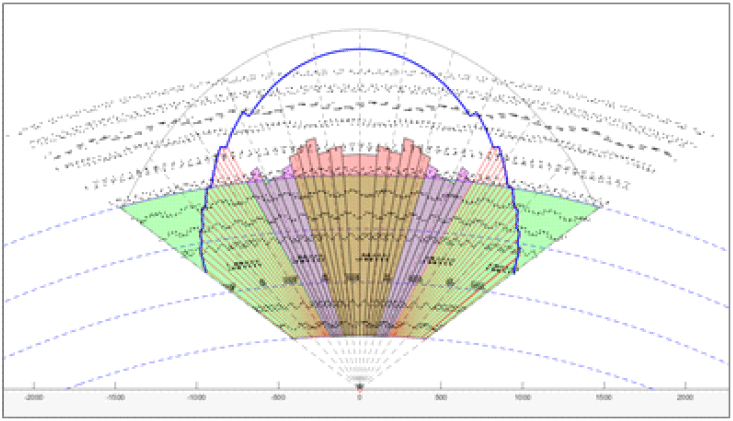
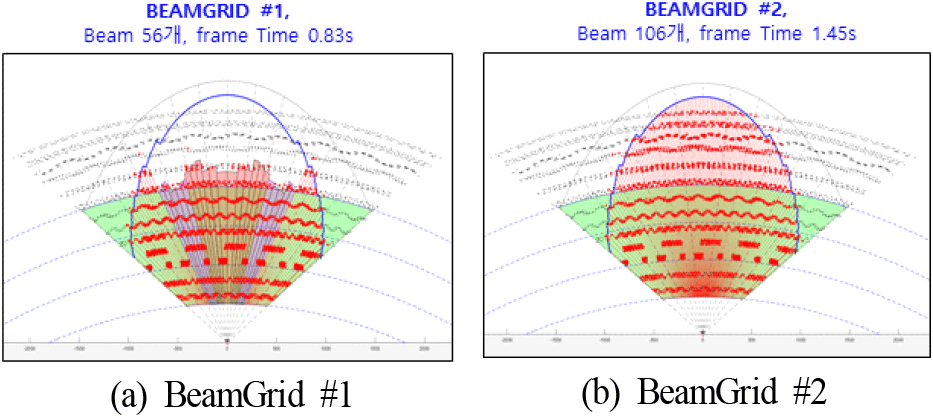
탐색 빔그리드는 앞절에서 설명한 빔 확장을 통한 빔그리드 최적화(BEAMGRID #1)와 모두 펜슬빔(BEAMGRID #2)으로 설정한 두 가지로 설정하고 모의하였으며, 모든 표적의 RCS 0.01 m2일 때 시뮬레이션을 통한 탐지결과를 다음의 그림에 빨간색 점으로 나타내었다.
그림 19에서 그림 19(a)는 빔 최적화를 통해 고도 1,000 km까지 탐지되는 것을 나타내며, 그림 19(b)은 Boresight에서 1,500 km까지 탐지가 가능하며 빔조향각에 따라 빔조향 손실만큼 탐지거리가 감소됨을 보여준다. 이 결과만 보면 전부 펜슬빔으로 구성하는 것이 성능이 좋게 보일 수 있지만 실제로 RCS가 작은 표적이 고도 1,000 km 이상 분포하지는 않을 것이므로 주어지는 요구사항에 맞게 빔그리드를 선택할 수 있다.
다음 그림 20에서는 빔그리드 형상에 따라 프레임 타임 변화로 인해 탐지/추적 개수를 시뮬레이션하기 위해서 동시에 여러 개의 표적이 들어오는 상황을 모의한 것이다. 공개된 TLE(two line element) 데이터를 사용하여 궤도를 생성하면 이러한 상황은 자주 발생하지는 않지만, 레이다에서 펜스를 설정해서 탐색한다는 것은 이미 알고 있는 표적이 아니라 우주 파편이나 미발견된 표적을 확인하기 위한 것이므로 실제로 다양한 상황에서의 대응을 위해서 동시에 진입하는 표적을 모의하였다.
레이다가 표적을 탐지/추적하는 과정은 펜스처럼 설정된 탐색 영역을 앞절에서 설계된 빔그리드 형상에 따라 순차적으로 스캔하고 각 빔에서 새로운 표적이 탐지되면 추적하는 과정을 거친다.
그림 21은 펜스를 통과한 이후 시뮬레이션을 통해 추적된 결과를 보여주며 왼쪽은 빔그리드 최적화한 경우의 결과를, 오른쪽은 기본 빔그리드로 설정한 경우에서의 결과를 안테나 좌표계(방위각, 고각)에서 나타낸 것이다.
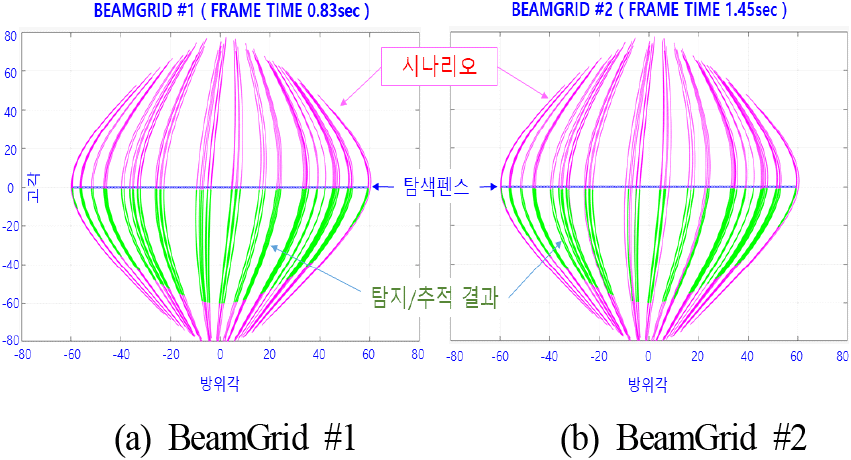
시뮬레이션 시간 동안 탐색 펜스를 총 92개의 위성이 통과하였고 이 중 빔그리드 별 탐지/추적된 결과는 표 2에 나타내었다.
| 분류 | BEAMGRID #1 | BEAMGRID #2 |
| 빔개수 | 56 | 106 |
| 프레임 타임 | 0.83 sec | 1.45 sec |
| 탐지/추적 수 | 88 | 74 |
펜스 통과 개수는 92개이지만 이 중 레이다 빔조향 범위를 벗어나거나 펜스를 통과하더라도 가장자리에 있어서 짧게 통과하는 경우는 추적이 어려우므로 총 92개 중 BEAMGRID #1에서는 88개를 탐지/추적하였고, BEAMGRID#2에서는 프레임 타임 증가로 74개를 탐지/추적하였다.
BEAMGRID#2를 적용하여 시뮬레이션한 결과 탐지/추적 개수이 안되고 놓친 모의 위성을 하나 살펴보면, 시나리오 상 설정된 값은 고도는 528 km이고 펜스 빔폭을 통과하는 시간은 약 0.96 sec이다(그림 22).
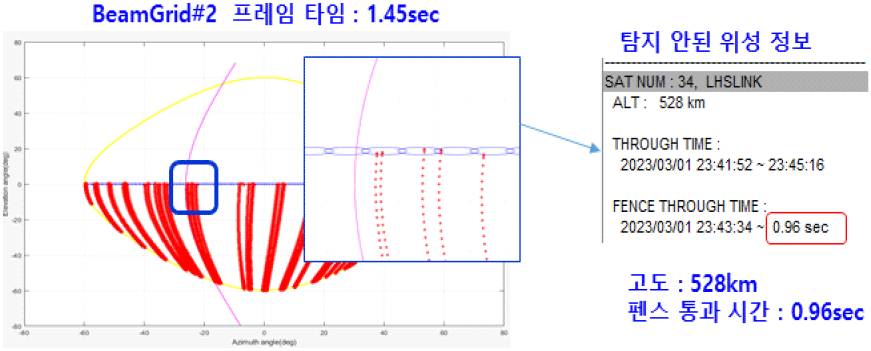
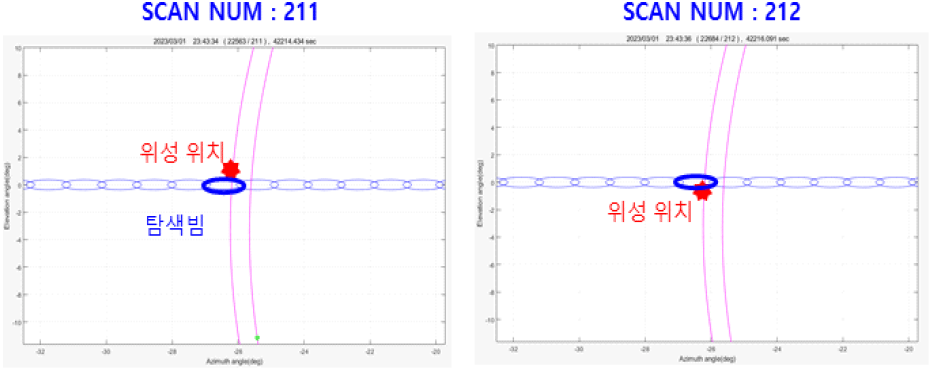
해당 위성이 탐색 펜스를 통과하는 시간은 스캔 번호 211~212 사이에 통과하는데 그 시점에서의 위성 위치가 이동함에 따라 탐색 빔도 이동하고 다음번 스캔 때에는 이미 지나가 버렸기 때문에 탐색 펜스를 통과하더라도 탐지/추적이 안된 것이다. 따라서 고도가 낮은 경우에는 빔폭을 벗어나는 시간이 더욱 짧아지므로 탐색 펜스를 통과하는 시간, 즉 프레임 타임을 줄이는 것이 매우 중요하다(그림 23).
IV. 결 론
본 연구에서는 우주감시레이다의 효율적 탐색을 위하여 탐지 영역을 설정하고 각 영역 별 탐지 성능을 만족하도록 탐색 빔그리드를 설계하는 알고리즘을 제안하였다.
제안한 방식은 전부 펜슬빔으로 설정한 기본 빔그리드를 형성한 후 각 빔조향각에서의 여유이득에 따라 빔 확장 방식을 선택하고, 기본 빔그리드 내에서 확장해 가는 방식으로 간단히 구성할 수 있다.
확장빔 방식으로는 위상가변 송신빔 확장과 주파수 다중빔 방식을 여유이득에 따라 적용하였으며, 최종 설계된 빔그리드 결과 원하는 탐지 범위 안에서 전체 탐색 빔개수 및 스캔 타임을 감소시킬 수 있었다.
설계된 빔그리드 형상을 적용하여 각 상황에 맞는 시나리오를 모의하고 레이다 시뮬레이션을 통해 탐지 성능 결과를 비교 분석하였다.
우주감시레이다와 같이 고출력의 대형 안테나를 운용하기 위해서는 자원을 효율적으로 사용해야 하므로 주어진 요구범위 내에서 탐색 영역을 설정하고 그 안에서 탐지 성능을 만족하는 빔그리드 형상을 적용함으로써 탐지 운용에 필요한 자원을 절약할 수 있을 것이다.