I. 서 론
FMCW(frequency modulated continuous wave) 레이다는 가격이 저렴하고, 가벼우며, 전력 소모가 적어 인원 계수 추정 시스템 및 비접촉 생체 신호 모니터링과 같은 다양한 분야에서 널리 사용된다. 특히, FMCW 레이다는 사생활 침해 우려가 없고, 시간의 변화에 영향을 받지 않아 실내 인간 위치 추적과 낙하 감지에도 사용되고 있다[1]~[4].
그러나, 실내에서 FMCW 레이다를 사용할 때 수신 데이터에는 표적의 정보뿐만 아니라 의자, 벽과 같은 정지 클러터와 멀티패스 신호도 포함된다. 이 멀티패스 신호는 정지 클러터에서 반사된 신호가 다른 정지 클러터를 거쳐 수신되는 정적 멀티패스 신호(static multipath signal)와 표적의 미세한 움직임에 의해 발생하는 동적 멀티패스 신호(dynamic multipath signal)로 나눌 수 있다. FMCW 레이다에 수신된 정지 클러터의 속도 성분은 0이고, 이로 인해 정지 클러터에 의해 발생한 정적 멀티패스 신호의 속도 성분도 0으로 볼 수 있다. 따라서 정지 클러터와 정적 멀티패스 신호는 지수 이동 평균(exponential moving average)으로 제거할 수 있다[5]. 하지만 동적 멀티패스 신호는 호흡이나 떨림처럼 표적의 미세한 움직임에 의해 발생하고, 그에 따라 0이 아닌 도플러 주파수 편이와 속도 성분을 갖게 돼 지수 이동 평균으로는 제거할 수 없는 문제가 있다. 또한, 각 정지 클러터마다 레이다 반사 면적(RCS, radar cross section)이 다르고 전파의 반사, 회절, 굴절이라는 특성으로 인해 동적 멀티패스 신호의 세기와 방향은 프레임마다 무작위로 변화해 표적 탐지 정확도가 떨어지는 문제가 있다[6].
동적 멀티패스 효과를 완화하기 위해서 지금까지 다양한 연구가 진행되었다[7]~[9]. 그러나 기존 연구는 두 개 이상의 FMCW 레이다를 사용해 추가적인 공간 및 비용이 필요한 한계가 있다. 또한, 동적 멀티패스 신호와 실제 표적을 거리-속도 맵 상에서 일치시키기 위해선 FMCW 레이다를 사용하는 장소의 환경 정보를 사전에 알아야 하는 어려움이 따른다. 그리고, 동적 멀티패스 신호는 프레임마다 그 세기와 방향이 무작위로 변화하기 때문에 동적 멀티패스 신호와 표적 신호의 관계는 비선형적이라고 볼 수 있다. 따라서, 실내 환경에서 단일 FMCW 레이다를 이용해 동적 멀티패스 효과를 효과적으로 완화할 수 있는 새로운 방법이 필요하다.
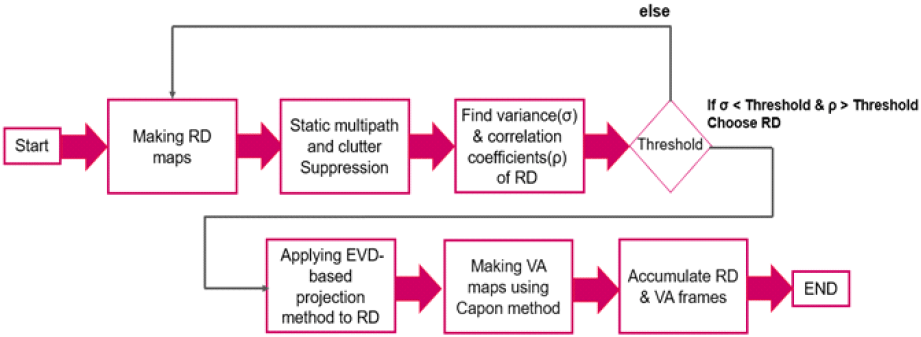
본 논문은 하나의 FMCW 레이다로 배경 정보 없이 동적 멀티패스 효과를 완화하는 방법을 그림 1과 같이 제안한다. 우선, FMCW 레이다 수신 데이터를 2차원 고속 푸리에 변환해 거리-속도 맵을 생성하고, 지수 이동 평균을 이용해 정지 클러터와 정적 멀티패스 효과를 완화한다.
정지 클러터의 영향이 감소된 전체 거리-속도 맵을 여러 프레임 그룹으로 나눈 뒤, 각 그룹에서 거리 축 분산값이 가장 작은 거리-속도 맵을 기준으로 선택한다. 거리-속도 맵에서 동적 멀티패스 효과가 적게 발생할수록, 표적의 위치에 에너지가 집중돼 거리 축 분산값이 작아지기 때문이다. 이후, 기준 거리-속도 맵과 같은 그룹에 속한 다른 거리-속도 맵들 사이의 상관 계수를 계산하고, 분산값과 상관 계수를 기반으로 임계값을 설정해 동적 멀티패스 효과가 강하게 나타나는 거리-속도 맵을 제외함으로써 신호 처리 효율성을 높인다.
다음으로, 그룹 내 남아있는 거리-속도 맵에 고유값 분해를 적용해 투영 행렬을 생성한 후, 거리-속도 맵들을 투영 행렬에 투영시켜 동적 멀티패스 신호를 완화한다.
만약 여러 표적이 비슷한 거리에 있다면, Capon 기법[10]을 통해 속도-각도 맵을 생성하면 다수 표적을 탐지할 수 있다. 마지막으로 그룹 내 거리-속도 맵과 속도-각도 맵에 비동기적 합성(non-coherent Integration)을 적용했다[11]. 제안 기법의 유효성을 검증하기 위해 실내 환경에서 실험을 진행한 결과, 기존 기법에 비해 신호 대 잡음비가 최대 18.7 dB 향상됐으며, 전체 프레임 계산 시간이 최대 12.47 % 감소됐고, 표적 탐지 성능이 개선되었고, 속도-각도 맵에서 부엽이 최대 2.4 dB 감소한 것을 확인하였다.
II. 제안 기법
시분할 다중화 FMCW 레이다는 그림 2에 나타난 것처럼 시간에 따라 주파수가 선형적으로 증가하는 처프 신호를 주기적으로 송신한다. 임의의 시간 t에서 송신 신호 s(t)는 식 (1)과 같이 표현할 수 있다.
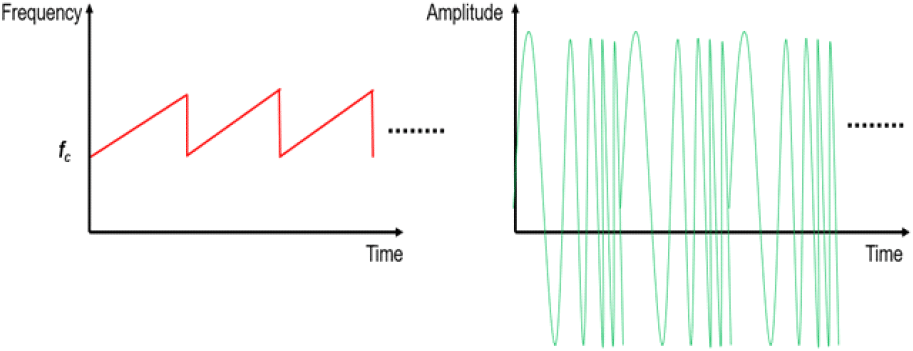
이때, fc는 중심 주파수, B는 대역폭, Tc는 처프 신호의 지속 시간이다. s(t)는 표적에서 반사돼 FMCW 레이다 수신기로 수신된 후, s(t)의 켤레 복소수 신호와 곱하고 저대역 통과 필터를 거쳐 중간 주파수(IF) 신호를 생성한다. 그리고 시간에 따른 연속적인 중간 주파수 신호를 ADC를 통해 이산 IF 신호 행렬 x[n, l, p]를 만들 수 있으며, 이는 식 (2)로 나타낼 수 있다[12].
여기에서 n은 샘플링 인덱스, l은 처프 인덱스, p는 수신기 인덱스, R은 FMCW 레이다와 표적 사이의 거리, v는 표적의 속도, Ts는 샘플링 주기, λ는 송신 신호의 파장, d는 FMCW 레이다 안테나 사이의 간격, θ는 수신 신호와 FMCW 레이다 수신기 안테나 사이의 각도, 그리고 φ는 여분의 위상 성분을 의미한다.
식 (2)를 통해 표적의 거리, 속도 그리고 각도 성분이 주파수에 비례함을 알 수 있다. 그러므로 수신 데이터의 거리와 속도 축을 따라 2차원 고속 푸리에 변환을 적용하면 거리-속도 맵을 생성할 수 있다. 또한, 각 프레임의 FMCW 레이다 수신 데이터는 서로 다른 x[n, l, p]를 가지므로, 여러 거리-속도 맵 프레임을 행렬 RD로 표현하면 식 (3)처럼 나타낼 수 있다.
여기에서 p는 수신기 인덱스, P는 전체 수신기 개수, a와 b는 각각 거리와 속도 축으로 제로 패딩과 함께 2차원 고속 푸리에 변환을 했을 때 셀의 개수, i는 프레임 인덱스, I는 전체 프레임 개수이다.
RD는 표적과 정지 클러터의 거리 및 속도 정보를 함께 갖고 있다. 또한, 정지 클러터에서 반사된 신호는 전파의 반사, 회절, 굴절 특성에 따라 다른 정지 클러터로 전달되기도 한다. 그 결과, 여러 정지 클러터를 거쳐 수신된 신호는 실제 정지 클러터의 거리보다 더 큰 거리값을 나타낼 수 있다. 이와 같이, FMCW 레이다 수신기에선 정지 클러터로부터 반사된 신호와 정지 클러터의 거리값이 왜곡된 신호를 함께 수신하는데, 정지 클러터의 실제 거리값과 달라진 이 신호를 정적 멀티패스 신호(static multipath signal)라고 정의한다[6].
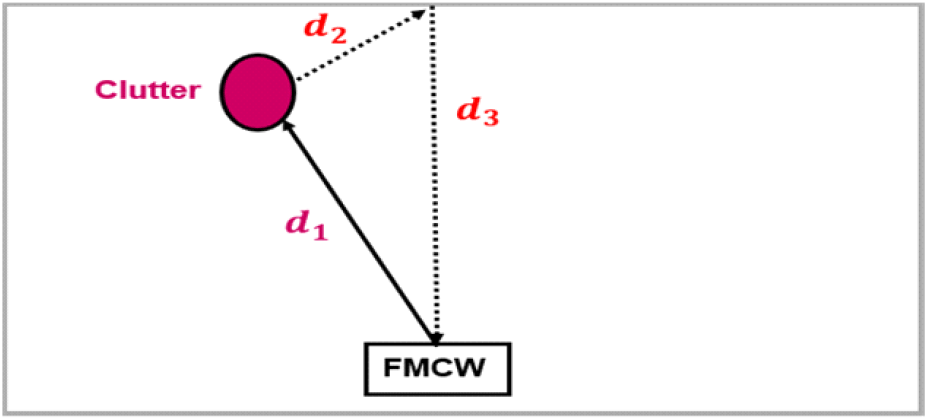
그림 3에서 보여지는 바와 같이, 정지 클러터와 FMCW 레이다 사이의 거리는 d1이지만, 다른 정지 클러터인 벽을 걸쳐서 반사된 결과, FMCW 레이다엔 d1+d2+d3의 거리값을 갖는 신호도 함께 수신된다. 실내 환경에선 정지 클러터들 사이의 거리가 실외보다 짧아 정적 멀티패스 효과가 자주 발생하며, 정지 클러터 신호의 세기가 표적 신호의 세기보다 강한 경우도 존재한다[13]. 따라서, RD에서 표적의 거리 및 속도 정보를 정확하게 탐지하기 위해선 정지 클러터와 정적 멀티패스 효과를 줄여야 한다.
정지 클러터는 정지해 있으므로 도플러 주파수 편이가 0이고, 그에 따라 2차원 고속 푸리에 변환을 적용했을 때 거리-속도 맵에서 정지 클러터의 속도 성분은 0으로 나타난다. 또한, 정적 멀티패스 신호는 기존의 정지 클러터의 수신 신호와 비교했을 때 거리 성분은 다르지만, 속도 성분은 동일하다. 하지만, 정지 표적의 맥박이나 호흡으로 발생하는 속도 성분은 거리-속도 맵에서 그 크기가 매우 작아 이동 표적 지시기(MTI, moving target indicator)[11]를 적용할 경우, 정지 클러터뿐만 아니라 표적의 정보도 함께 제거될 가능성이 있다. 그러므로 정지 클러터의 영향을 최소화하면서 정지 표적만을 남기는 기법이 필요하다.
지수 이동 평균(EMA)[5]은 이전 거리-속도 맵에 가중치를 반영해 정지 클러터를 제거하는 기법이다. 현재 프레임에서의 정지 클러터 정보는 이전 프레임의 정지 클러터 정보와 현재 프레임에서의 거리-속도 맵을 가중 평균해 지속적으로 업데이트된다. 임의의 p번째 수신기에서 i번째 거리-속도 맵 프레임 에 지수 이동 평균을 적용하면 식 (4)처럼 나타낼 수 있다.
여기에서 는 에 지수 이동 평균을 적용한 결과이고, α는 0과 1 사이의 값을 갖는 파라미터다.
i번째 거리-속도 맵 프레임에서 식 (5)를 통해 정지 클러터와 정적 멀티패스가 완화된 거리-속도 맵 프레임 를 얻을 수 있다.
이때, 정적 멀티패스 완화 전후의 주파수 전달 함수를 구하기 위해 식 (5)를 정리해 식 (6)처럼 나타낼 수 있고,
식 (6)을 식 (4)에 대입하면 식 (7)로 표현할 수 있다.
주파수 전달 함수 H(z)를 구할 수 있다.
이 때, H(z)는 z=α에서 극점을, z=1에서 영점을 갖는 고대역 통과 필터이다. 따라서, 지수 이동 평균을 사용하면 주파수 성분이 없는 정지 클러터와 정적 멀티패스 효과가 차단되고, 맥박이나 호흡으로 인해 상대적으로 고주파 성분을 갖는 정지 표적의 속도 성분은 남게 된다.
식 (4)를 전체 수신기와 프레임에 적용하면 RD에서 정지 클러터와 정적 멀티패스 효과를 완화한 RD’를 식 (9)와 같이 나타낼 수 있다.
표적의 호흡, 맥박, 떨림과 같은 미세한 움직임으로 인해반사 신호의 진행 경로가 바뀌어 정지 클러터를 거치게 되는 경우가 발생할 수 있다. 그 결과, 반사 신호는 여러 정지 클러터를 거치면서 기존 반사 신호의 거리와 각도 성분이 왜곡된 상태로 FMCW 레이다 수신기로 수신되며, 이렇게 거리와 각도 성분이 왜곡된 신호를 동적 멀티패스 신호(dynamic multipath signal)라고 정의한다. 동적 멀티패스 신호는 정적 멀티패스 신호와 유사하게, 각 정지 클러터마다 서로 다른 RCS와 전파의 특성에 의해 프레임마다 크기와 방향이 무작위로 변화한다[11].
그림 4에서 정지 표적과 FMCW 레이다 수신기 사이의 거리와 각도 성분이 각각 d1, θ1로 나타나며, 표적의 맥박과 호흡으로 인해 속도 v1이 발생하는 것을 보여준다. 이러한 미세한 움직임으로 인해 표적으로부터 반사된 신호의 진행 경로가 변하게 되고, 이는 정지 클러터를 거쳐서 FMCW 레이다로 수신된다. 그 결과, FMCW 레이다는 d1+d2+d3의 거리와 θ2라는 각도 성분을 갖는 동적 멀티패스 신호를 함께 수신하게 된다.
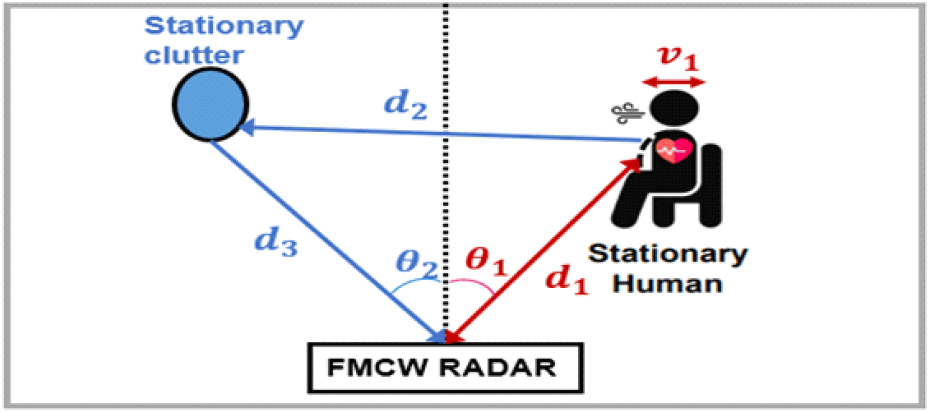
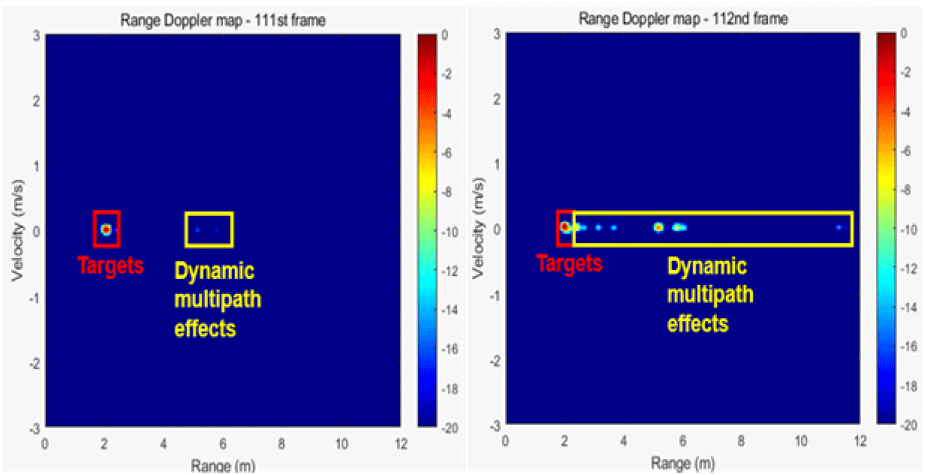
그림 5는 실내에서 정지한 두 표적을 FMCW 레이다로 측정하고 얻은 수신 데이터로 거리-속도 맵을 생성해 동적 멀티패스 효과가 프레임마다 무작위로 발생하는 것을 설명하는 그림이다. 지수 이동 평균을 통해 거리-속도 맵의 정지 클러터와 정적 멀티패스 효과를 완화했지만, 표적의 미세한 움직임으로 인해 0이 아닌 속도 성분을 갖는 동적 멀티패스 효과는 제거되지 않음을 볼 수 있다. 그리고 벽, 의자, 책상과 같은 여러 정지 클러터로 인해 표적으로부터 반사된 신호의 거리와 방향이 매 프레임마다 무작위로 변화함을 알 수 있다.
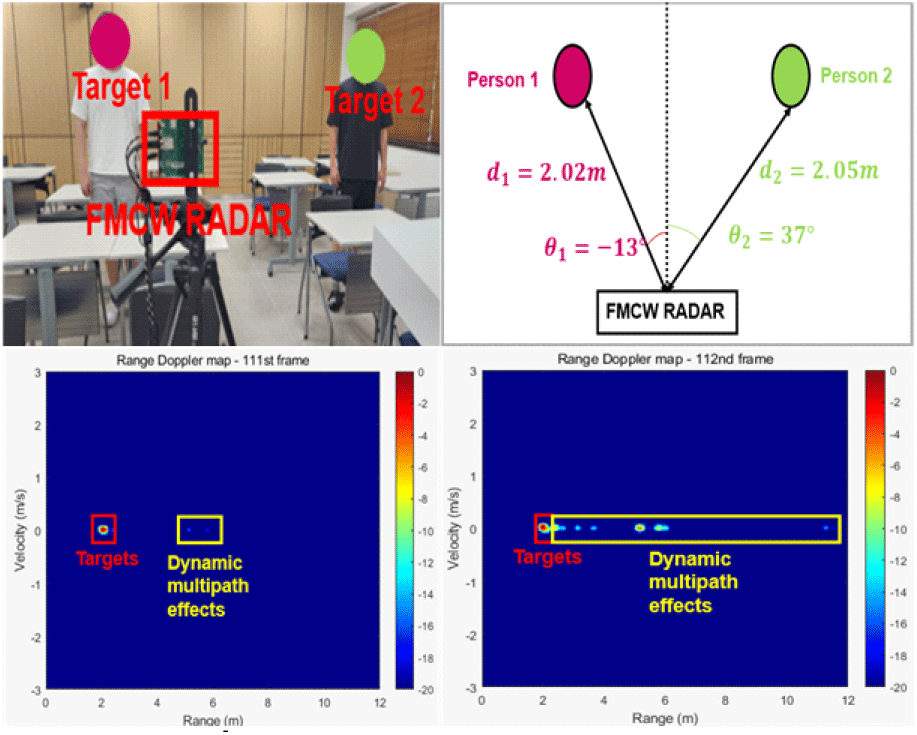
동적 멀티패스 효과는 정지 클러터 간의 거리가 짧은 실내에서 빈발하는 경향이 있고, 그 세기가 표적 신호의 세기보다 강할 때도 있다[11]. 따라서, 정적 멀티패스 신호뿐만 아니라 동적 멀티패스 효과의 신호도 완화해야만 표적의 정보를 정확하게 탐지할 수 있다.
기술한 바와 같이, 동적 멀티패스 효과는 프레임마다 발생하는 위치와 크기가 다르므로, 기존 기법들처럼 모든 프레임을 일괄적으로 처리하는 방식엔 한계가 있다. 또한, 불필요한 데이터 처리로 인해 하드웨어에 부담이 가중되며, 처리 시간도 많이 소요되는 단점이 있다.
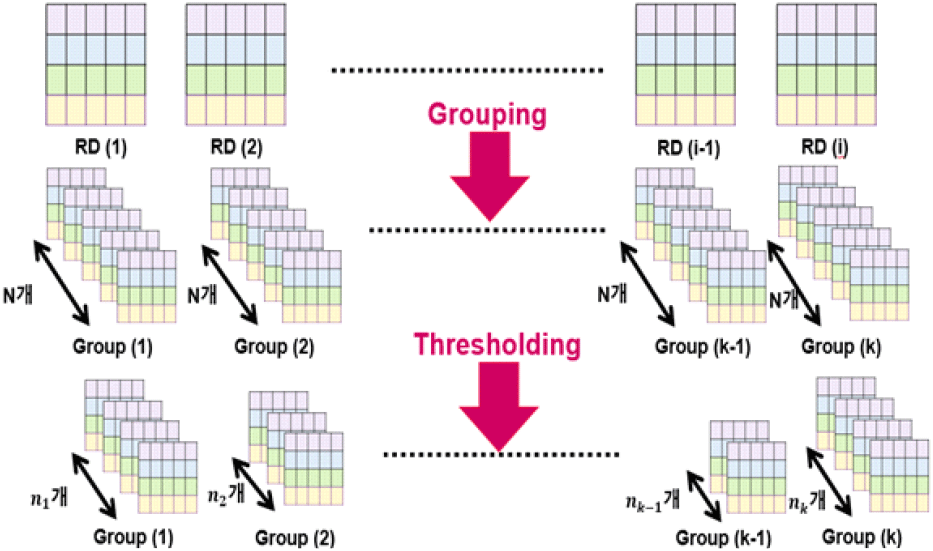
따라서 본 논문에서는 그림 6과 같이 총 I개의 프레임으로 이루어진 전체 거리-속도 맵을 N개의 거리-속도 맵을 단위로 나누어, k개의 그룹을 형성한다. 그리고 각 그룹마다 임계값을 설정해 그룹 내부에서 선택된 nk개의 프레임에 대해서 신호 처리하는 기법을 제안한다. 이를 통해 하드웨어의 부담을 줄일 수 있을 것이다.
RD’을 임의의 정수 N개 단위로 그룹화하면 총 k개의 그룹을 만들 수 있고, 이를 식 (10)처럼 나타낼 수 있다.
그룹 내부에 있는 임의의 거리-속도 맵에서 동적 멀티패스 효과가 거리 축으로 길게 발생하고 그 세기가 강하다면, FMCW 레이다의 송신 전력이 한정돼 있으므로 거리 축으로 에너지가 분산될 것이다. 이로 인해, 해당 거리-속도 맵의 거리 축 분산값은 증가하는 경향을 보일 것이다. 따라서, 그룹 내에서 거리 축 분산값이 가장 작은 거리-속도 맵은, 거리 축으로 동적 멀티패스 신호가 가장 적게 발생했으며 그 세기도 작다고 판단할 수 있다. 각 그룹의 거리 축 분산값 행렬 은 식 (11)과 같이 표현 된다.
이때, 는 RDp’(kN)의 거리 축 분산값이고, dp,j(kN)와 μp,d(kN)는 각각 RDp’(kN)의 거리 축 데이터와 그 평균값이다.
분산값이 가장 작은 거리-속도 맵을 기준으로 그룹 내부의 다른 거리-속도 맵들과의 상관 계수를 비교한다면, 해당 거리-속도 맵에서 동적 멀티패스 효과가 얼마나 발생했는지를 평가할 수 있다. 분산값이 가장 작은 거리-속도 맵을 RDp’a×b(s), 그 거리 축 분산값을 라고 할 때, 상관 계수 행렬 ρ는 식 (12)로 나타낼 수 있다.
식 (11) 및 식 (12)를 이용해 임계값을 설정하면, 그룹 내에서 동적 멀티패스 신호의 세기가 크고, 거리 축으로 길게 발생한 거리-속도 맵을 신호 처리 시 제외할 수 있다. 의 평균과 표준 편차를 μσ와 σσ라고 하고 ρ의 평균과 표준 편차를 μρ,와 σρ라고 할 때, 동적 멀티패스 신호가 강할수록 값은 증가하고 ρ는 감소할 것이다. 이에 따라, 적절한 가중치 α와 β를 곱해 임계값 εσ와 ερ를 설정하면 식 (13)의 두 가지 조건을 도출할 수 있다.
이후, 식 (13)을 식 (10)에 적용하면 각 그룹 내 N개의 거리-속도 맵 중에서 동적 멀티패스 신호가 상대적으로 강한 N-nk개의 맵을 제외하고, 신호 처리할 nk개의 거리-속도 맵을 선택할 수 있다. 그 결과는 행렬식으로 식 (14)와 같이 표현할 수 있다.
그림 7은 그림 5의 실험 결과에서, N(=10)개의 거리-속도 맵으로 구성된 그룹 중 세 번째 그룹인 21번째 프레임부터 30번째 프레임에 대해, 식 (11)~식 (14)까지의 과정을 거쳐 신호 처리할 n(=6)개의 거리-속도 맵을 분류하는 과정을 설명한다. 좌측 그림은 동적 멀티패스 효과가 거의 발생하지 않아 식 (11)에 의해 분산값이 그룹 내에서 가장 낮다. 따라서 좌측 그림을 기준으로 삼아 그룹 내부 다른 거리-속도 맵들과 비교하는 식 (12)의 과정을 거친다. 우측 그림은 동적 멀티패스 효과가 거리 축으로 길게 발생해 가 높고, 좌측 그림과의 ρ가 낮아 식 (13)에 따라 해당 맵은 그룹 별로 신호 처리 시 제외한다.
식 (13) 및 식 (14)는 그룹 내에서 동적 멀티패스 효과가 강하게 발생한 거리-속도 맵을 제외하는 역할을 하지만, 이는 동적 멀티패스 효과를 근본적으로 완화하는 방법이 아니다. 그러므로, 본 논문에서는 그룹 내에서 신호 처리할 프레임에 고유값 분해(EVD, eigen value decomposition)[14]를 적용해 동적 멀티패스 효과를 줄이고자 한다.
고유값 분해란 임의의 m×m 복소수 정사각 행렬을 고유벡터(S)와 대각선에 고유값을 갖는 고유값 벡터(Λ)로 대각화하는 기법이다. 복소수 정사각 행렬 A를 식 (15)처럼 대각화할 수 있다.
만약 식 (3)에 거리 축과 도플러 축으로 제로 패딩의 개수를 m개로 동일하게 설정하면, 그룹 내 신호 처리할 거리-속도 맵에 고유값 분해를 적용할 수 있다. 식 (13)에 의해 각 그룹마다 설정된 임계값이 다르므로, 그룹마다 nk개의 열 벡터를 갖고 있다. 임의의 Group(k)의 첫 번째 열 벡터 a1는 식 (16)과 같이 표현되며,
이는 특정 프레임에서 각 수신기에서의 거리-속도 맵을 나타낸다. a1의 거리 축으로 공분산 행렬을 구하고, 공분산 행렬에 대해 고유값 분해를 적용하면 식 (17)처럼 나타낼 수 있다.
공분산 행렬의 가장 큰 고유값 λp에 가장 많은 에너지가 담겨 있다고 볼 수 있다[15]. 식 (11)~식 (14)까지를 이용해 각 그룹에서 동적 멀티패스 효과가 강하게 발생한 프레임을 제외하고, 표적의 세기가 동적 멀티패스 효과보다 강한 프레임만을 그룹에 남겨 놓았다. 즉, 공분산 행렬의 λp와 그에 해당하는 고유 벡터 SP에는 거리-속도 맵 상에 있는 표적의 에너지가 집증되어 있다고 예측할 수 있다. 투영 행렬은 식 (18)과 같이 구할 수 있으며, 여기에서 H는 에르미트 연산자(Hermitian operator)이다.
그림 8의 좌측은 식 (11)~식 (14)까지를 이용해 그림 5의 결과 그룹 내에서 동적 멀티패스 효과가 상대적으로 약한 거리-속도 맵을 선택한 결과를, 우측은 이 거리-속도 맵에 식 (17) 및 식 (18)을 전체 거리 축과 속도 축에 적용해 생성된 투영 행렬을 시각화한 것이다. 시각화된 투영 행렬에 나타난 것처럼 실제 표적의 위치에 에너지가 집중되어 있고, 동적 멀티패스 효과가 발생한 영역엔 상대적으로 적은 에너지가 분포해 있음을 알 수 있다.
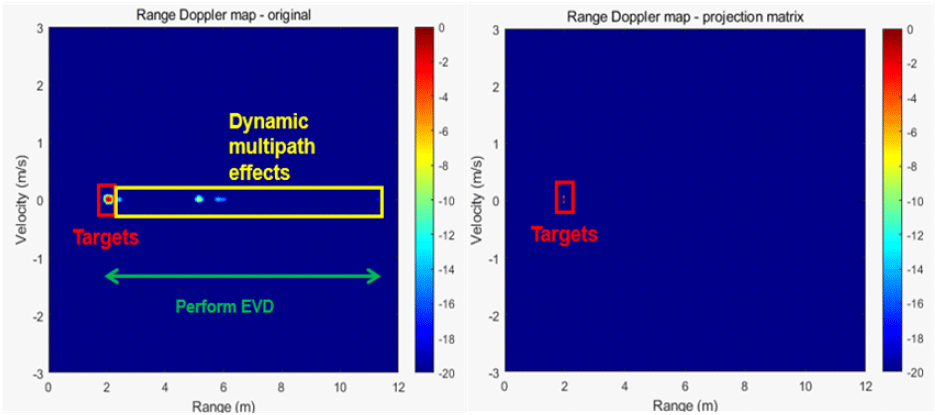
또한, 그림 4에 의해 동적 멀티패스 효과는 실제 표적의 위치보다 먼 거리에서 발생하고, 고유값 분해로 인한 연산 시간을 감소시키기 위해 표적의 에너지가 가장 큰 거리로부터 일정 범위까지 고유값 분해를 적용했다.
이후, RD’p×m{(k−1)N+1}와 식 (18)에서 생성한 투영 행렬 간에 아다마르 곱(Hadamard product)을 적용하면 첫 번째 거리 셀에서 동적 멀티패스 효과가 완화된 RD*p×m{(k−1)N+1}을 만들 수 있고, 이를 거리 축 전체에 적용하면 동적 멀티패스 효과가 완화된 열 벡터 a1*을 식 (19)와 같이 표현할 수 있다.
여기에서 ⊙는 아다마르 연산자(Hadamard operator)다.
다음으로 식 (18) 및 식 (19)를 각 그룹 내 nk개의 열 벡터 및 전체 그룹에 적용하면, 동적 멀티패스 효과가 완화된 RD*을 식 (20)처럼 만들 수 있다.
그림 9는 그림 5의 결과를 동적 멀티패스 효과 완화하기 전후의 거리-속도 맵을 비교한 결과이다. 기존 거리-속도 맵은 동적 멀티패스 효과가 거리 축으로 길게 발생했지만, 제안 기법을 통해 동적 멀티패스 효과가 완화돼 표적의 거리와 속도값만 남아있음을 확인할 수 있다.
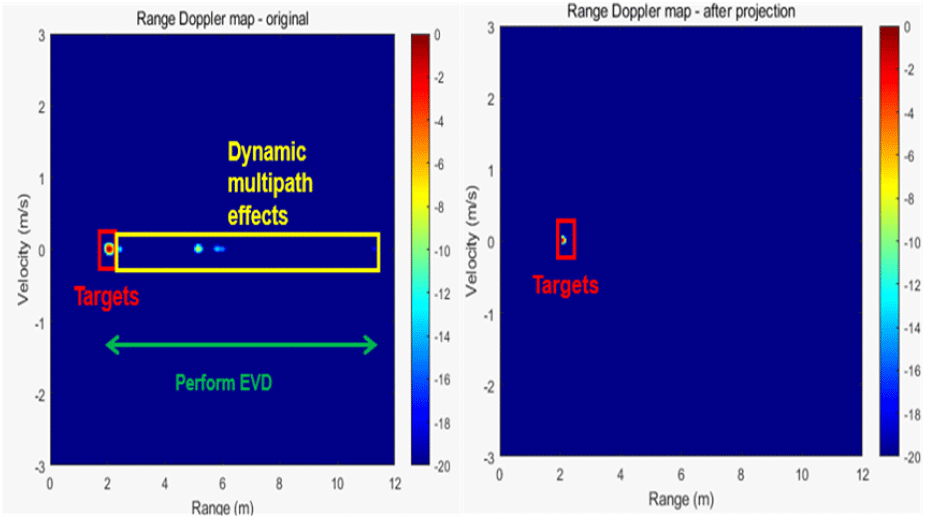
그러나, 실내에 여러 표적이 비슷한 거리에 정지해 있다면 거리-속도 맵만으로는 여러 표적을 탐지하는 데 어려움을 겪을 수 있다. 또한, FMCW 레이다는 하드웨어적인 제약으로 인해 대역폭이 한정되어 있어 거리 해상도가 제한된다. 그 결과, 여러 정지 표적이 인접해 있다면 거리-각도 맵으로도 표적들의 거리와 각도 정보를 파악하기 어려울 수 있다. 이를 해결하기 위해, 한 프레임 당 처프의 개수를 올려 속도 해상도를 향상시킨 다음, 식 (20)을 이용해 속도-각도 맵을 생성한다면, 비슷한 거리에 인접해 있는 여러 정지 표적을 탐지할 수 있을 것이다.
그러나, 2차원 고속 푸리에 변환을 이용해 속도-각도 맵을 생성할 경우, 상용 FMCW 레이다의 제한된 수신기 개수로 인해 각도 해상도가 좋지 않고, 부엽이 커져 여러 표적을 구분하기 어렵게 된다[16]. 이러한 문제를 극복하기 위해 다중 신호 분류(MUSIC, multiple signal classification) 알고리즘[17]이나 추정 신호 매개변수 회전 불변 기법(EPRIT, estimation of signal parameters via rotational invariance techniques)[18] 등이 제안됐지만, 이러한 기법들은 모델 오더 선택 문제의 한계를 갖고 있다. 반면, Capon 기법[10]은 모델 오더 선택 문제로부터 자유롭다는 장점이 있어, 이를 이용해 속도-각도 맵[11]을 생성하면, 2차원 고속 푸리에 변환을 이용한 경우보다 각도 해상도를 개선할 수 있을 것이다[19].
Capon 기법을 적용하기 위해 지향 행렬 B를 식 (21)과 같이 생성한다.
여기에서 bθRX,p는 p번째 수신기에서의 지향 행렬이다. 그리고 식 (19)의 열 벡터의 속도 축으로 식 (22)와 같이 Capon 기법을 적용하면, {(k−1)N+1}번째 프레임에서의 속도-각도 맵을 생성할 수 있다.
이 때, pm은 m번째 속도 셀에서 VA{(k−1)N+1}의 공간 스펙트럼이고, Im은 m×m 단위 행렬, tr은 대각합 연산자, α는 상수이다.
이후, 식 (22)를 식 (20)에 적용하면, 각 그룹마다 서로 다른 nk개의 속도-각도 맵을 갖는 k개 그룹의 전체 속도-각도 맵 행렬 VA를 식(23)과 같이 생성할 수 있다.
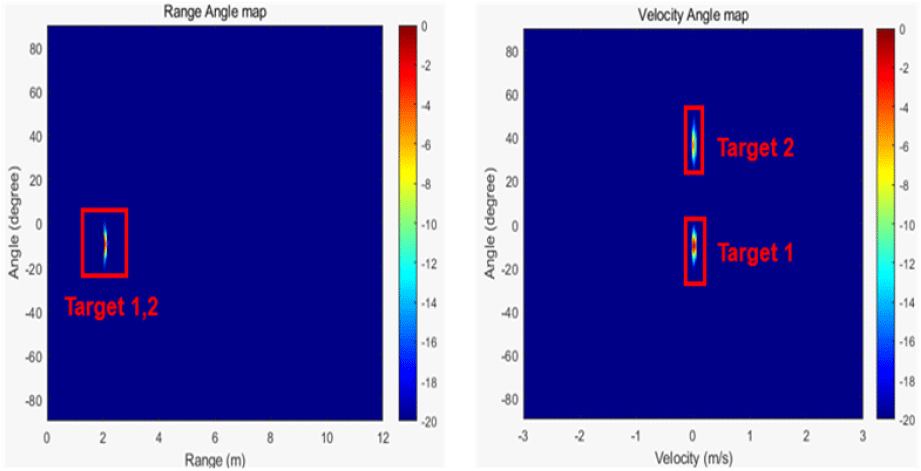
그림 10은 식 (20)에 Capon 기법을 적용해 그림 5의 거리-각도 맵과 속도-각도 맵을 보여준다. FMCW 레이다로부터 두 표적의 거리가 비슷하고, 제한된 대역폭으로 인해 거리 해상도가 좋지 않아 거리 축에서 인접한 두 표적을 거리-각도 맵에서는 구분하기 어렵다. 하지만, 한 프레임당 처프의 개수를 올려 속도 해상도가 향상시킨 결과, 속도-각도 맵을 통해선 두 표적을 명백히 구분할 수 있음을 알 수 있다.
FMCW 레이다와 표적 간 거리는 수신기 간 거리보다 훨씬 크므로, 각 수신기에 수신되는 표적의 거리와 속도 값은 유사하다고 볼 수 있다. 따라서, 식 (20)을 수신기 축으로 더하는 비동기적 합성을 취하면 하나의 거리-속도 맵일 때 보다 신호 대 잡음비(SNR, signal to noise ratio)를 향상시킬 수 있다.
또한, 식 (20) 및 식 (23)에 있는 각 그룹 내 서로 다른 nk개의 프레임을 그룹별로 비동기적 합성을 적용하면, 신호 대 잡음비를 추가적으로 증가시킬 수 있을 것이다[11].
신호 대 잡음비는 식 (24)를 통해 구할 수 있다.
그림 11은 그림 5의 결과인 식 (20) 및 식 (23)의 그룹 중 하나를 선택하여, 비동기적 합성 전후의 변화를 비교한 것이다. 처음 룹 내부 프레임의 개수(N)는 10이었지만, 식 (11)~식 (14)까지를 이용해 동적 멀티패스 효과의 세기가 강하면서 거리 축으로 길게 발생한 프레임을 제외한 결과, 그룹 내부 프레임의 개수(nk)는 6으로 감소했다.
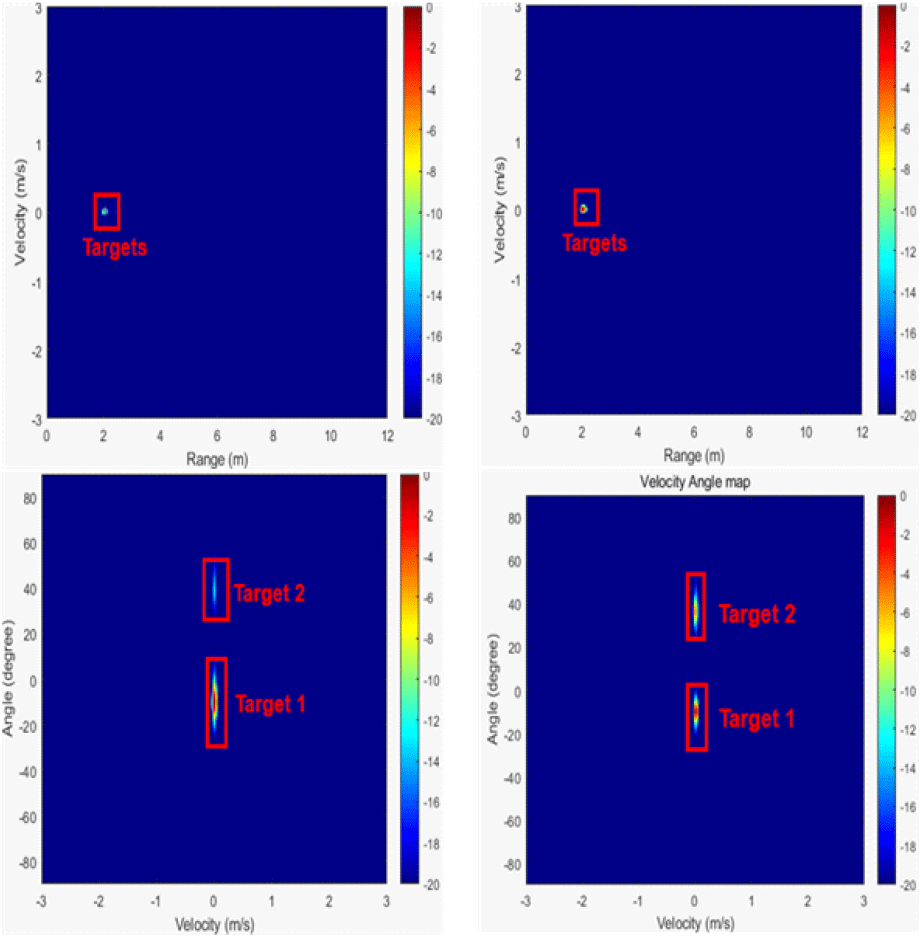
좌측 상단의 거리-속도 맵은 그룹 내 하나의 거리-속도 맵이고, 우측 상단은 거리-속도 맵들을 수신기 축으로 더한 다음, 그룹 내부의 거리-속도 맵들을 더한 비동기적 합성 결과이다. 이로 인해 거리-속도 맵에서 표적 신호의 세기가 강해졌음을 알 수 있고, 신호 대 잡음비는 5.64 dB가량 증가했다.
좌측 하단의 속도-각도 맵은 좌측 상단의 거리-속도 맵에 식 (22)를 적용한 결과이고, 우측 하단은 그룹 내부에 있는 거리-속도 맵들에 식 (22)를 적용한 다음, 비동기적 합성을 거친 결과이다. 그 결과, 속도-각도 맵에서 표적 2의 세기가 강해졌음을 파악할 수 있으며, 신호 대 잡음비는 4.91 dB 증가했다. 또한, 비동기적 합성을 거치면서 부엽은 0.56 dB 감소하였다.
III. 실측 실험
제안 기법의 유효성을 검증하기 위해서 두 가지 실험을 진행했다. 첫 번째 시나리오는 한 명의 표적이 실내에 정지해 있는 상태였으며, 두 번째 시나리오는 두 표적이 레이다 피탐 면적이 넓은 벽 바로 앞에 서 있는 상태였다. 두 실험 모두 20초간 측정했으며, 실험에 사용된 FMCW 레이다 구성은 표 1에 나타내었다.
첫 번째 실험은 실내에서 한 명의 정지 표적을 대상으로 FMCW 레이다로 측정한 실험이었고, 이를 그림 12에 도식화했다. 피측정자는 (1.1 m, −4°)에 정지해 있었으며, 정지 클러터인 책걸상 및 벽으로 인해 정적 및 동적 멀티패스 효과가 발생할 것을 예측할 수 있다.
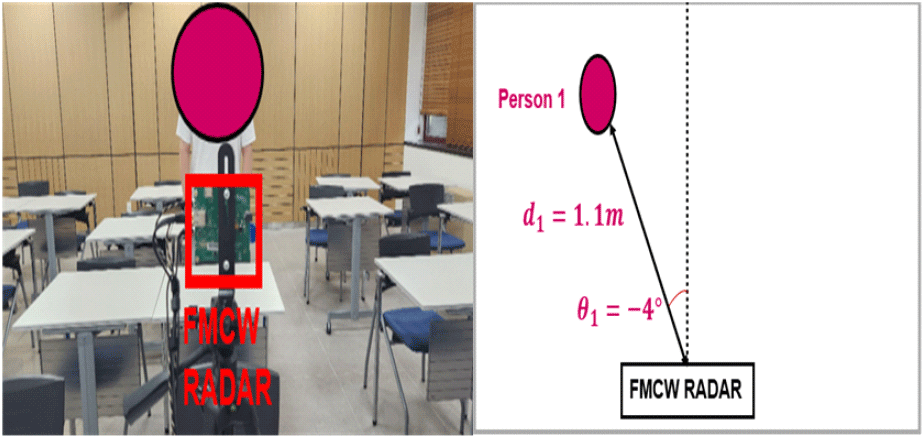
그림 13은 참고문헌 [11]에서 제안한 기법을 적용한 후, 41번째부터 50번째까지 프레임을 비동기적 합성한 거리-속도 맵과 속도-각도 맵이다. 해당 논문에선 정지 클러터에 의한 영향을 이동 표적 지시기(moving target indicator)를 통해 최소화한 뒤, 거리-속도 맵과 속도-각도 맵을 비동기적 합성을 취한 다음, MD-CLEAN 알고리즘을 이용해 거리-속도 맵과 속도-각도 맵에서 표적을 탐지하는 기법을 제시했다. 그러나, 동적 멀티패스 효과가 강하게 발생한 프레임까지 비동기적 합성에 포함시킨 결과, 거리-속도 맵에서 오탐지가 발생함을 관찰할 수 있다. 또한, 동적 멀티패스 효과로 인해 수신 신호에선 표적의 실제 각도 값과 각도가 왜곡된 값을 함께 갖기 때문에, 속도-각도 맵에서 표적 주위로 부엽이 길게 발생했음을 알 수 있다.
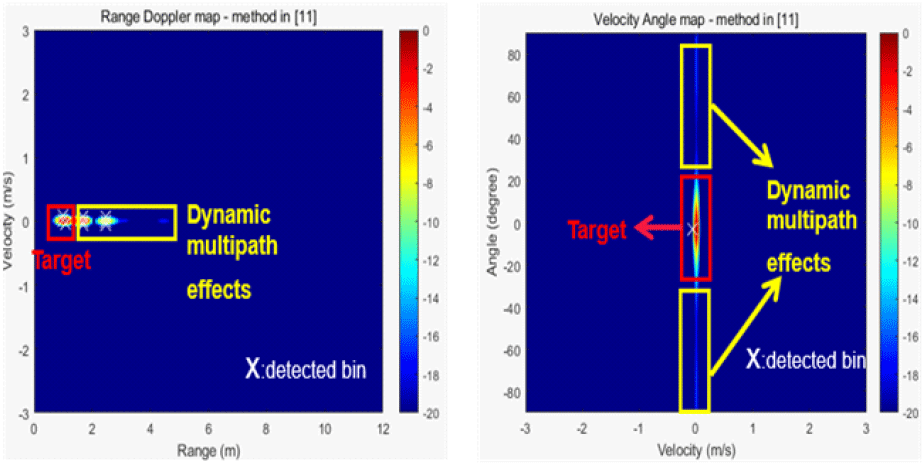
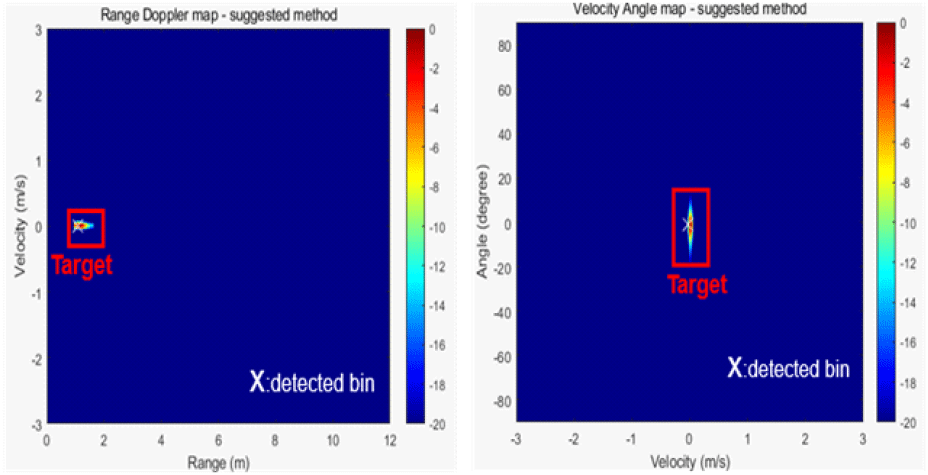
그림 14는 본 논문에서 제안한 기법을 적용한 거리-속도 맵과 속도-각도 맵이다. 식 (10)~식 (14)번을 이용해 총 200개의 프레임을 10개의 거리-속도 맵을 갖는 그룹으로 나누고, 임계값을 이용해 동적 멀티패스 효과가 강한 프레임을 그룹에서 제외했다. 그 결과, 이 그룹에 속한 41번째 프레임부터 50번째 프레임까지, 총 6개의 거리-속도 맵이 선택됐고, 식 (16)~식 (24)를 적용한 후, 속도-각도 맵을 생성하고 각 맵에 비동기적 합성을 적용했다. 그 결과, 거리-속도 맵에서 오탐지가 발생하지 않았으며, 속도-각도 맵에서 부엽이 1.72 dB 감소하였다.
두 번째 실험은 실내에 정지해 있는 두 명의 사람을 측정했고, 이를 그림 15에 도식화했다. 이 실험에선 표적과 레이다 사이 거리가 멀어졌으며, 표적 주위에 레이다 피탐 면적이 큰 벽이 있어 정지 클러터 신호의 세기가 표적의 신호보다 큰 경우가 발생할 수 있다. 또한, 표적과 레이다 사이 더 많은 책상과 의자들을 배치해 첫 번째 실험보다 멀티패스 효과가 빈발하도록 설정했다. 표적들 사이의 거리를 거리 해상도인 0.0834 m보다 짧게 설정했고, 표적은 (4.1 m, −15°)와 (4.08 m, 39°)에 정지해 있었다.
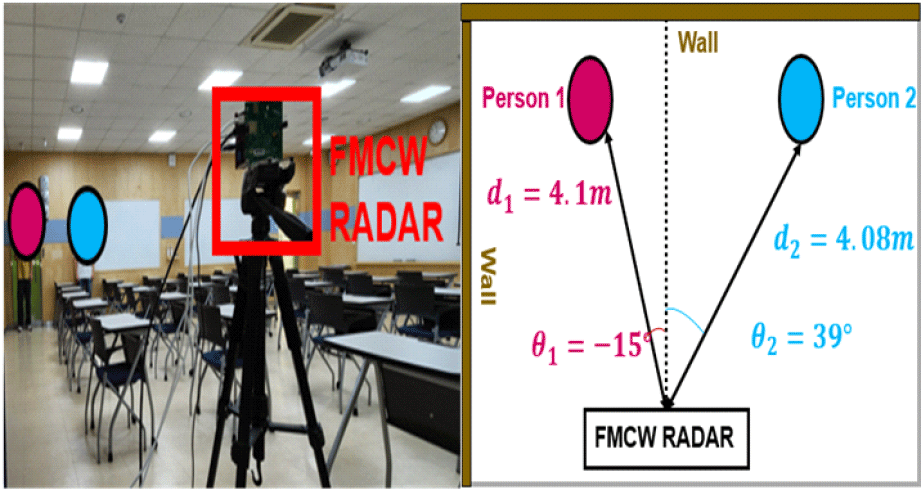
그림 16은 두 번째 실험 결과를 참고문헌 [11]에서 제안한 기법으로 생성한 거리-속도 맵과 속도-각도 맵이다. 71번째 프레임부터 80번째 프레임까지 총 10개의 거리-속도 맵과 속도-각도 맵에 비동기적 합성을 적용한 뒤 MD-CLEAN 알고리즘을 적용했지만, 표적 주위에 레이다 피탐 면적이 큰 벽이 있었고, 첫 번째 실험에 비해 책상과 의자가 많아져 동적 멀티패스 효과의 세기가 표적보다 강해지고, 거리 축으로 빈발한 것을 관찰할 수 있다. 그에 따라 실험 1의 결과에 비해 오탐지가 증가하였다.
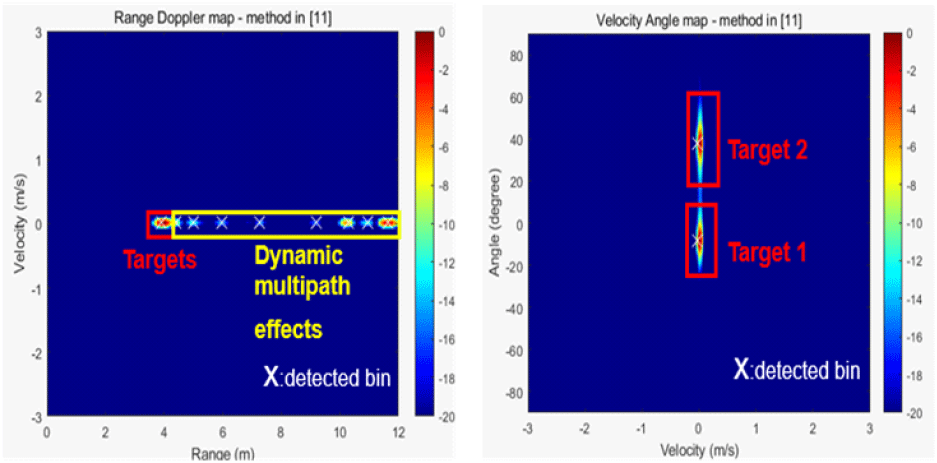
그림 17은 본 논문에서 제안한 기법을 두 번째 실험에 적용해 생성한 거리-속도 맵과 속도 각도 맵이다. 식 (10)~식 (14)번을 이용해 200개의 전체 프레임을 각 그룹마다 10개의 거리-속도 맵을 갖는 그룹으로 나누었다. 그리고 임계값을 적용한 결과, 이 그룹인 71번째 프레임부터 80번째 프레임까진 총 4개의 거리-속도 맵이 선택됐다. 이후, 식 (16)~식 (24)를 적용해 동적 멀티패스 효과를 완화하고 속도-각도 맵을 생성한 다음, 그룹 내부에서 비동기적 합성을 적용했다. 그 결과, 거리-속도 맵에서 오탐지를 줄이고, 표적을 정확하게 탐지했으며, 속도-각도 맵에선 부엽이 2.21 dB 감소했음을 확인하였다.
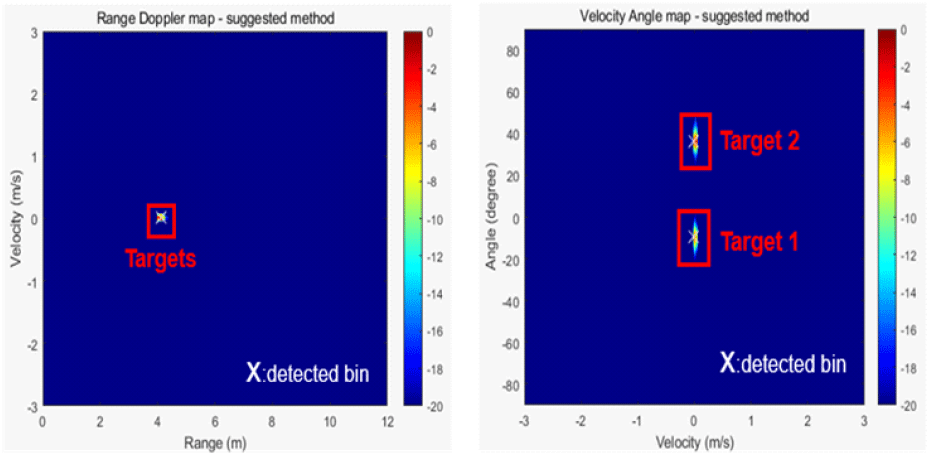
그림 18은 참고문헌 [11]에서 제안한 기법과 본 논문에서 제안한 기법의 신호 대 잡음비(SNR)를 비교한 그림이다. 상단의 좌측과 우측 그림은 각각 실험 1의 거리-속도 맵과 속도-각도 맵의 신호 대 잡음비 그래프이다. 그리고 하단의 좌측과 우측 그림은 각각 실험 2의 거리-속도 맵과 속도-각도 맵의 신호 대 잡음비 그래프이다. 또한, 청색 그래프는 참고문헌 [11]에서 제안한 기법을 적용한 경우의 신호 대 잡음비를 계산했을 때 그래프이고, 적색은 본 논문에서 제안한 기법으로 신호 대 잡음비를 계산했을 때의 그래프이다.
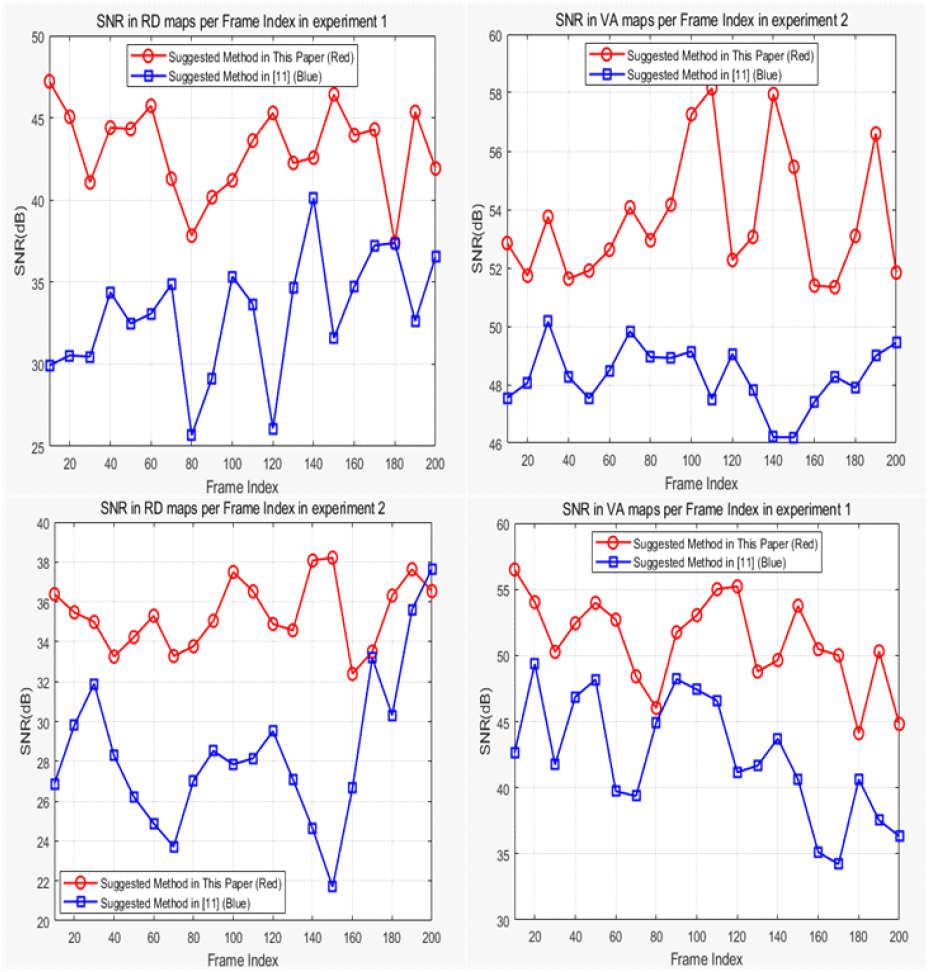
제안 기법을 통해 각 그룹마다 10개의 거리-속도 맵을 갖도록 설정했으며, 그룹별로 임계값을 다르게 설정해 각 그룹에서 서로 다른 개수의 거리-속도 맵이 선택됐다. 각 그룹의 거리-속도 맵에 제안 기법을 적용한 결과, 그룹 내에서 일부 프레임이 제외됐는데도 불구하고 신호 대 잡음비가 대부분 그룹에서 향상됐음을 확인할 수 있다.
그림 19는 참고문헌 [11]의 기법과 본 논문의 기법을 거리-속도 맵에서 MD-CLEAN 알고리즘을 사용했을 때의 탐지 성능과 속도-각도 맵에서 부엽을 비교한 그림이다. 상단의 좌측과 우측 그림은 각각 실험 1의 프레임 그룹마다 거리-속도 맵에서의 탐지 성능과 속도-각도 맵에서의 부엽의 정도를 나타낸다. 그리고 하단의 좌측과 우측 그림은 각각 실험 2의 프레임 그룹마다 거리-속도 맵에서의 탐지 성능과 속도-각도 맵에서의 부엽의 정도를 비교한 그림이다. 또한, 청색 그래프는 참고문헌 [11]에서 제안한 기법의 결과이고, 적색 그래프는 본 논문에서 제안한 기법의 결과이다.
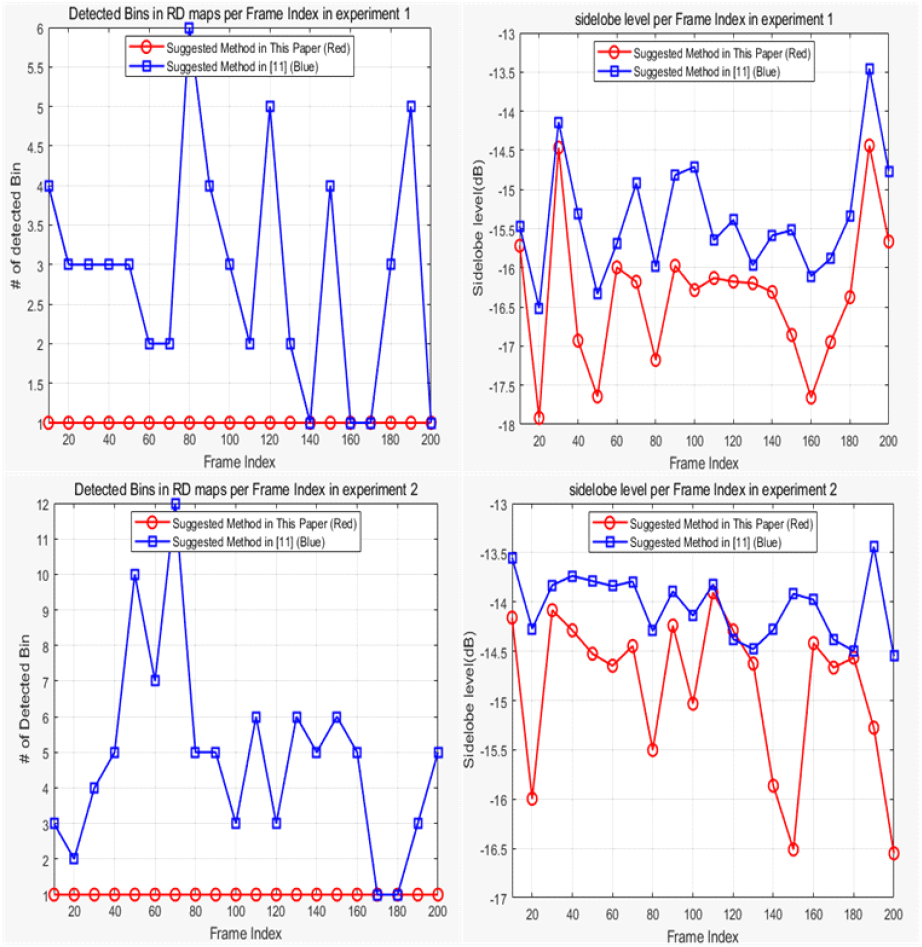
참고문헌 [11]에서 제안한 기법은 그룹 내 거리-속도 맵끼리 비동기적 합성을 적용할 때, 동적 멀티패스 효과도 함께 더해져 전체 프레임에서 오탐지가 빈번하게 발생함을 확인할 수 있다. 반면, 제안 기법은 거리-속도 맵에서 동적 멀티패스 효과를 줄여 표적만을 남겼기 때문에 모든 프레임에서 표적 탐지가 정확하게 이루어진 것을 확인할 수 있다. 또한, 제안 기법을 통해 표적의 각도 정보의 정확성을 향상시켰으므로 속도-각도 맵의 대부분 그룹에서 부엽의 정도가 감소했음을 확인할 수 있다.
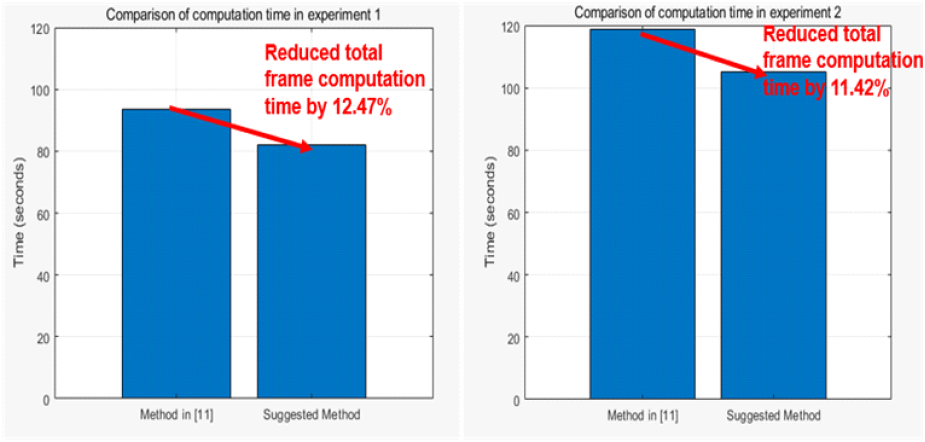
그림 20은 참고문헌 [11]에서 제안한 기법과 본 논문에서 제안한 기법의 전체 프레임 계산 시간을 비교한 그래프이다. 실험 1과 2에서 참고문헌 [11]에서 제안한 기법은 전체 프레임을 계산하는 데 각각 93.74초와 118.72초가 소요됐다. 그에 반해, 본 논문에서 제안한 기법은 임계값에 따라 일부 프레임만 계산함으로써, 실험 1과 2에서 각각 82.05초와 105.16초가 소요됐다. 결과적으로 제안한 기법은 기존 기법에 비해 전체 프레임 계산 시간이 최대 12.47 %가량 감소시켰고, 이는 실시간 처리나 계산 자원이 제한된 환경에서 제안 기법이 유용함을 시사한다.
IV. 결 론
본 논문에서는 지수 이동 평균을 통해 정지 클러터의 영향을 줄인 전체 거리-속도 맵을 일정한 개수의 그룹으로 나눈 뒤, 각 그룹에서 거리 축 분산값이 가장 작은 거리-속도 맵을 기준 삼아 그룹 내의 다른 거리-속도 맵들의 거리 축 분산값과 상관 계수를 기반으로 임계값을 설정해 그룹 내에서 신호 처리할 거리-속도 맵을 선택하였다. 이후, 선택된 거리-속도 맵에 고유값 분해를 적용해 투영 행렬을 생성한 다음, 기존 거리-속도 맵을 투영 행렬에 투영시킴으로써 동적 멀티패스 효과를 완화하는 방법을 제안하였다. 또한, 여러 표적이 비슷한 거리에 있는 경우 속도-각도 맵을 생성한 다음, 각 그룹 내부에 비동기적 합성을 적용하는 과정을 거쳤다.
제안 기법을 통해 모든 그룹의 거리-속도 맵에서 동적 멀티패스 효과가 효과적으로 완화되었으며, 기존 기법에 비해 거리-속도 맵에서의 탐지 정확성을 향상시켰고, 속도-각도 맵에서 부엽을 최대 2.4 dB 감소시켰다. 또한, 거리-속도 맵과 속도-각도 맵의 신호 대 잡음비 역시 제안 기법을 통해 각각 최대 18.7 dB 증가시킬 수 있었다. 더불어, 제한 기법을 통해 일부 프레임만을 계산함으로써 전체 프레임 계산 시간도 최대 12.47 % 감소시켰다.
따라서, 실내 사람 추적이나 비접촉 생체 신호 측정에 제안 기법을 적용한다면, 기존 기법보다 적은 시간 내에 표적의 정보를 더욱 정확히 파악할 수 있을 것이다. 특히, 동적 멀티패스 효과가 빈번히 발생하는 차량 내부 측정 데이터에 제안 기법을 적용한다면, 탑승자들의 위치 및 생체 신호를 파악하는 데도 도움이 될 것이다.