Ⅰ. 서 론
무선전력전송(wireless power transfer, WPT) 시스템은 그 안전성과 편리함으로 인해 많은 곳에 사용되고 있다[1]∼[3]. WPT 시스템은 송신(transmitter side, TX) 측과 수신(receiver side, RX) 측의 전기적 결합 없이, 자기장의 형태로 에너지를 전달할 수 있는 시스템이다. 따라서, TX 측과 RX 측이 물리적으로 분리되어 편리한 WPT 시스템은 다양한 어플리케이션에 사용되고 있다. 대표적인 어플리케이션으로는 모바일 어플리케이션, 전기자동차, 전기 철도, automated guided vehicle(AGV) 등이 있으며, 이미 상용화되었거나, 상용화를 위한 연구에 박차를 가하고 있다.
WPT 시스템은 자기장의 형태로 TX에서 RX로 에너지가 전달되기 때문에, TX 측과 RX 측이 자기장으로 결합하는 구조인 자기장 커플러(magnetic coupler) 구조가 매우 중요하다. 다양한 어플리케이션에 적용되기 위해 많은 커플러 구조가 개발되었는데, 대표적으로 사용되는 구조는 동심원을 가지는 두 개의 코일인 단극성(single sided) 코일, 2개의 극성을 한번에 가지는 DD 코일, 그리고, 자성체를 이용해 2개 극성을 통해 에너지가 전달되는 양극성 커플러 구조 등이 있다[3]∼[5]. 각각의 구조는 장점과 단점을 모두 가지며, 어플리케이션의 구조와 요구 성능에 따라 적절한 커플러 구조를 채택해야 한다.
그중에서, 양극성 커플러 구조는 그림 1(a)와 같은 구조를 가진다. 그림 1(b)에서처럼 TX 코일과 RX 코일이 서로 마주보는 형태인 단극성 코일들과는 달리 양극성 커플러 구조는 자성체가 마주보는 방향과 수직한 코일 방향으로 기자력을 생성한다. 코일에서 발생한 기자력은, 자성체를 통과하여 자성체의 양끝에서 TX에서 RX로 자기장이 전달된다. 단극성 코일들은 전력전송 효율이나 용량이 코일의 단면적에 강하게 의존하는데 비해, 양극성 코일은 비교적 좁은 면적의 공간에서도 자기장이 TX에서 RX로 충분히 쇄교할 수 있는 장점을 가진다. 따라서, 양극성 커플러를 사용하는 어플리케이션은 그 종류가 점점 늘어나고 있다[3].
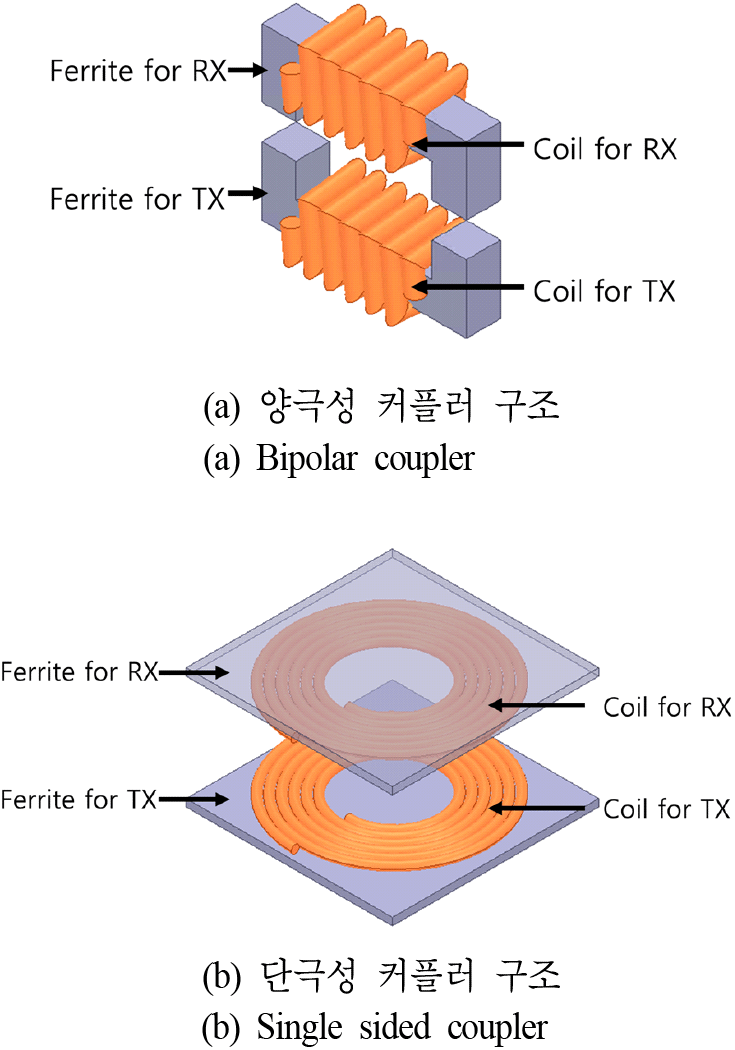
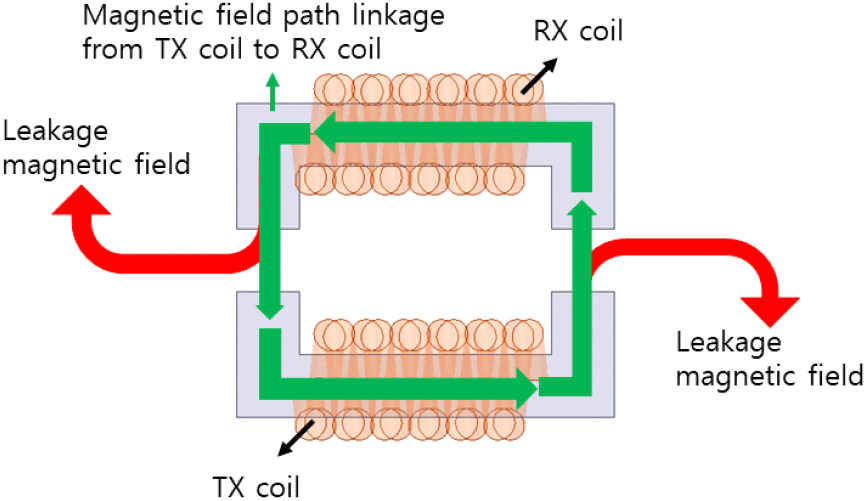
하지만, 양극성 커플러 구조가 본격적으로 상용화되는데 큰 걸림돌이 있는데, 바로 누설자기장 문제이다[4]. 그림 2와 같이 양극성 커플러 구조는 자기장의 누설 방향이 자성체 양방향으로 방사되는 구조를 가질 수밖에 없는데, 이로 인해 TX에서 RX로 쇄교되는 자속 이외에 누설자속이 발생한다. 따라서 자기장 인체영향 문제가 있을 수 있으며, 주변 기기에 영향을 끼치는 EMI 문제가 발생할 수 있다. 따라서, 주변 외함 등과의 자기적 결합으로 인한 손실 증가로 인해, 양극성 커플러의 쓰임새는 매우 제한적이었다. 이를 방지하기 위해서 알루미늄 차폐 구조 등을 채택하였지만, 이는 시스템의 손실을 증가시키는 등 많은 부작용이 따랐다[4]. 따라서, 양극성 커플러 구조가 상용화되기 위해서는 누설 자기장으로 인한 다양한 문제들이 해결되어야 한다[4].
본 논문에서는 양극성 커플러 구조의 누설 자기장 저감을 위하여 페라이트 격벽 구조에 대해 분석하였다. 무선전력전송 시스템에서 필요한 TX 코일에서 RX 코일로의 자기장 이외에 주변으로 누설되는 자기장을 저감하기 위하여 별도의 페라이트 격벽구조를 적용하였으며, TX 코일과 RX 코일 간의 결합계수(coupling coefficient)는 감소는 최소화하여 유지하면서 누설 자기장을 최대로 감소시킬 수 있는 구조를 제안하였다. 제안된 양극성 커플러 구조를 위한 격벽은 자기저항(reluctance) 모델로 분석되었으며, 시뮬레이션과 실험을 통해 그 효용성이 증명되었다.
본 논문의 구성은 아래와 같다. Ⅱ장에서는 제안된 양극성 커플러를 위한 페라이트 격벽에 대한 분석을 하며, Ⅲ장에서는 시뮬레이션을 통해 최적화된 격벽 구조를 설계하며, Ⅳ장에서는 실험을 통해 실제로 제안된 격벽구조를 통한 WPT 시스템의 누설 자기장의 저감을 증명하며, 전력전송 효율의 변화도 분석한다. 마지막으로 Ⅴ장에서 본 논문의 결론을 맺는다.
Ⅱ. 양극성 커플러 구조의 누설 자기장 저감을 위한 페라이트 격벽 구조
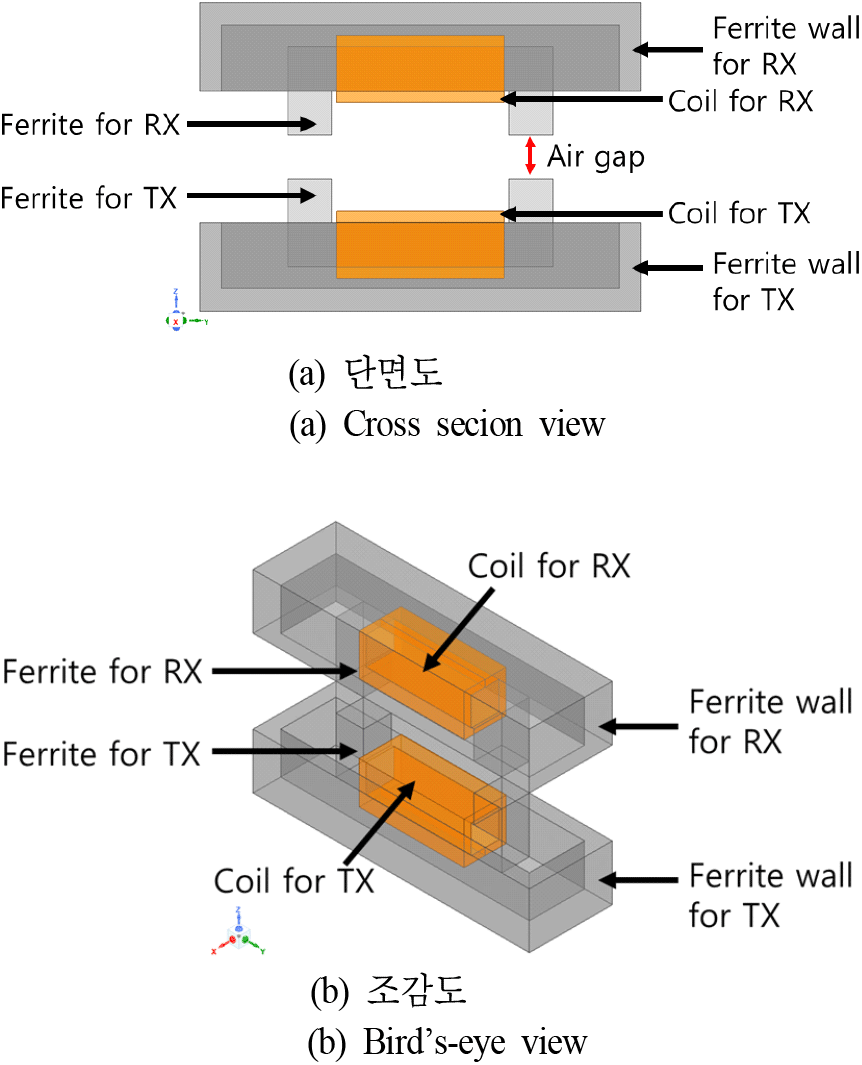
본 논문에서 제안 및 분석하기 위한 페라이트 격벽 구조를 가지는 양극성 커플러는 그림 3과 같다. 그림 3에서 알 수 있듯이, 기존의 양극성 커플러가 내부에 위치하고,외부에 자기장 차폐를 위하여 자기장 격벽 구조를 추가하였다. 이로 인해 무선전력전송을 위한 자기장 커플러에서 생성된 자기장 중에서, 누설 자기장이 페라이트 격벽에 집중되어, 외부로 누설되는 것이 최소화되는 장점을 가진다.
이를 자기저항 모델로 분석하기 위하여 그림 4의 등가자기저항(reluctance) 회로를 분석하였다. TX 코일에서 발생한 자기장이 RX 코일에 얼마나 쇄교하는지를 분석하기 위하여 TX 코일의 기자력(magneto-motive force)만을 고려하였다. TX 코일의 기자력은 식 (1)과 같다.
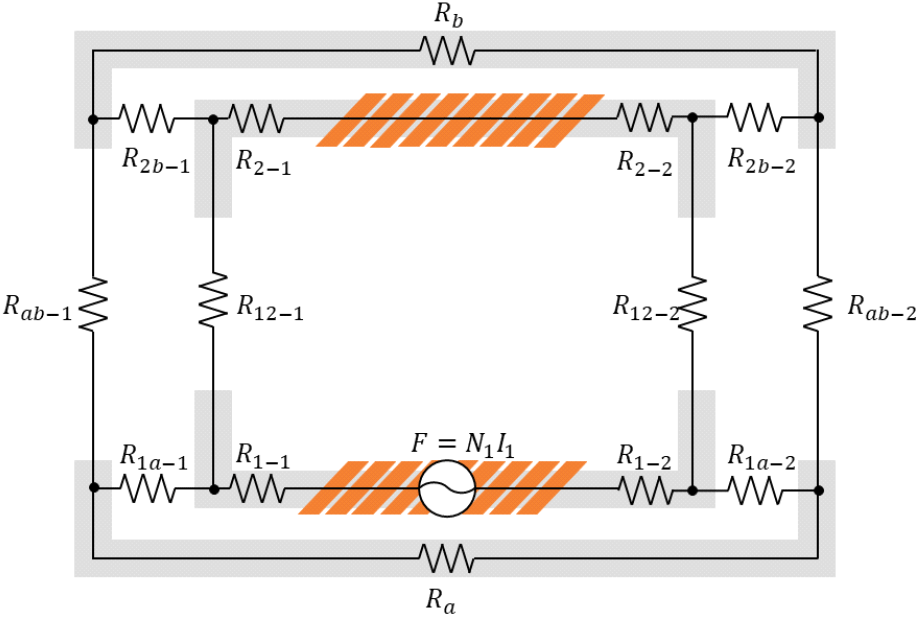
식 (1)에서, F는 TX 코일에 의한 기자력이며, N1과 I1은 각각 TX 코일의 턴 수와 TX 코일에 흐르는 전류이다. 또한, 모든 자기저항은 식 (2)와 같이 정의된다.
식 (2)에서 R은 자기저항이며, l은 등가 자로(magnetic path)의 길이, μ은 물질의 투자율, 그리고 A는 자로의 단면적이다. 공기 중에서는 비투자율이 1이며, 페라이트의 비투자율은 3,200이라고 가정한다.
기존의 양극성 커플러 구조에서는 페라이트 격벽 구조가 없기 때문에, TX와 RX 사이의 자기저항인 R12-1과 R12-2를 통해 흐르지 않는 자속은 모두 누설자속이 된다. 하지만, 그림 4와 같이 페라이트 격벽이 존재하는 경우에는 누설자속이 R1a-1과 R1a-2(혹은, R2b-1과 R2b-2)에 의해 페라이트 격벽으로 흡수된다. 따라서, 페라이트 격벽 외부에서는 누설 자기장이 감소될 것이라는 것을 예상할 수 있다.
하지만, 그림 3과 같이 페라이트 격벽 구조가 양극성 자기장 커플러 구조 근처에 존재하면, TX 코일에서 발생한 자기장이 RX 커플러로 쇄교되지 않고, TX 격벽로 모두 쇄교될 수 있다. 만약, TX 코일에서 발생한 자기장이 TX 격벽으로 모두 쇄교되면, RX 측으로 에너지가 전달되지 못하는 문제점이 발생한다. TX 코일에서 RX 코일로 쇄교되는 자기장이 최대가 되어야 WPT 시스템으로 인한 에너지가 효율적으로 전달될 수 있다. TX 코일에서 RX 코일로 쇄교되는 자기장이 최대가 되기 위해서는, 그림 4에서 R12-1과 R12-2가 매우 작아야 한다. 그림 1(a) 및 그림 2와 같은 기존의 양극성 커플러 구조에서는 단순히 자로의 길이, 즉 WPT 시스템의 공극에 의존하게 된다.
하지만, 본 논문에서 제안한 그림 3과 그림 4의 WPT 커플러의 경우에는 TX 페라이트와 TX 페라이트 격벽 사이의 자기 저항인 R1a-1과 R1a-2(혹은 R2b-1과 R2b-2)가 존재하게 된다. R1a-1, R1a-2에 의해 TX에서 RX로 쇄교되어야할 자기장이 TX에서 TX 페라이트 격벽으로 쇄교되는 문제점이 발생한다. 따라서, 본 논문에서 제안한 자기장 차폐를 위한 페라이트 격벽구조를 양극성 커플러에 적용하기 위해서는 커플러 코어를 위한 페라이트와 페라이트 격벽 사이의 자기저항을 적절히 조절하여야 한다.
이를 인덕턴스 모델에 적용하기 위하여 자기 인덕턴스와 상호 인덕턴스의 수식을 식 (3) 및 식 (4)와 같이 나타낸다.
식 (3) 및 식 (4)에서 L과 M은 각각 코일의 자기 인덕턴스와 상호 인덕턴스이며, Λ11, Λ12는 각각 TX 측에서 생성된 자속이 TX 코일 자체에 쇄교한 자속, RX 코일에 쇄교한 자속을 나타낸다. 마지막으로 I1은 TX 코일에 흐르는 전류이다. TX에서 RX로 쇄교되는 자속이 많을수록 식 (4)에 의해서 상호 인덕턴스가 커지는 것을 알 수 있다. 기존 연구들에 의하면, 상호 인덕턴스가 커지면 에너지가 효율적으로 전달된다[6],[7]. 하지만, TX 코일에 의해 생성된 자속이 페라이트 격벽으로 전달되면, TX에서 RX로 쇄교자속 Λ12는 감소하고, TX 자체 쇄교자속 Λ11은 증가한다. 즉, 상호 인덕턴스는 감소하고, 자기 인덕턴스는 증가하게 된다.
한편, TX 측과 RX 측의 자기적 결합강도를 나타내는 결합계수는 식 (5)와 같다.
식 (5)에서 k는 TX와 RX 사이의 결합계수이며, L1, L2는 각각 TX와 RX 코일의 자기 인덕턴스이다. 즉, 페라이트 격벽이 추가되면 코일들의 자기 인덕턴스는 증가하고, 상호 인덕턴스는 감소하여, 식 (5)에 의해 WPT 시스템의 자기 결합계수도 감소하게 된다.
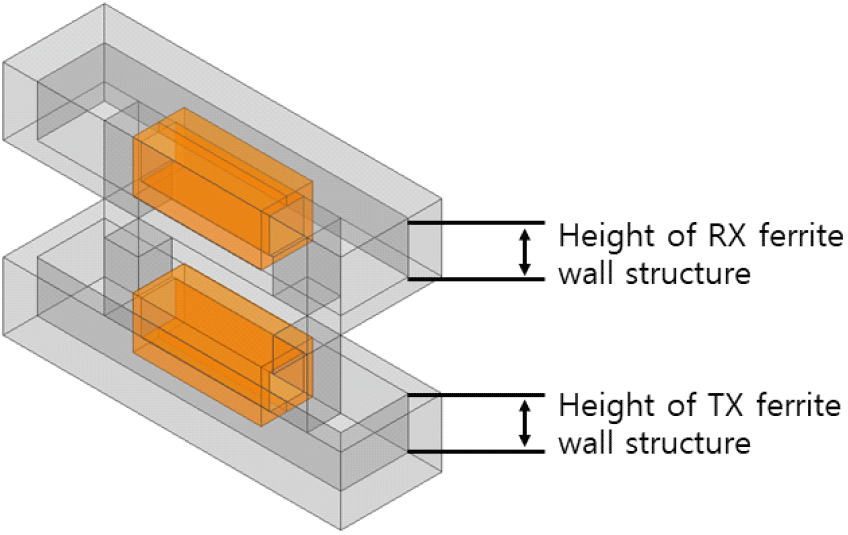
따라서, 자기장 저감을 위한 페라이트 격벽을 추가하면서도, 일정 이상의 결합계수를 확보할 필요가 있다. 이를 위해서는 자기장 커플러의 페라이트와 자기장 차폐를 위한 페라이트 격벽 사이의 자기저항을 적절히 조절해야 하는데, 이를 위해 본 논문에서는 그림 5와 같이 페라이트 격벽의 높이를 조절한다. 페라이트 격벽의 높이를 조절하게 되면, 양극성 커플러 구조와 페라이트 격벽이 마주보는 면적이 줄어들게 되며, 이는 식 (2)에서 자로의 면적(A)이 감소하는 효과를 갖는다. 이어지는 3장에서는 시뮬레이션을 통해 페라이트 격벽의 높이에 따른 양극성 커플러의 상호 인덕턴스와 자기 인덕턴스의 변화를 분석하여 최적의 페라이트 격벽 구조를 설계한다.
Ⅲ. 시뮬레이션을 통한 자기장 격벽구조 설계 및 누설 자기장 분석
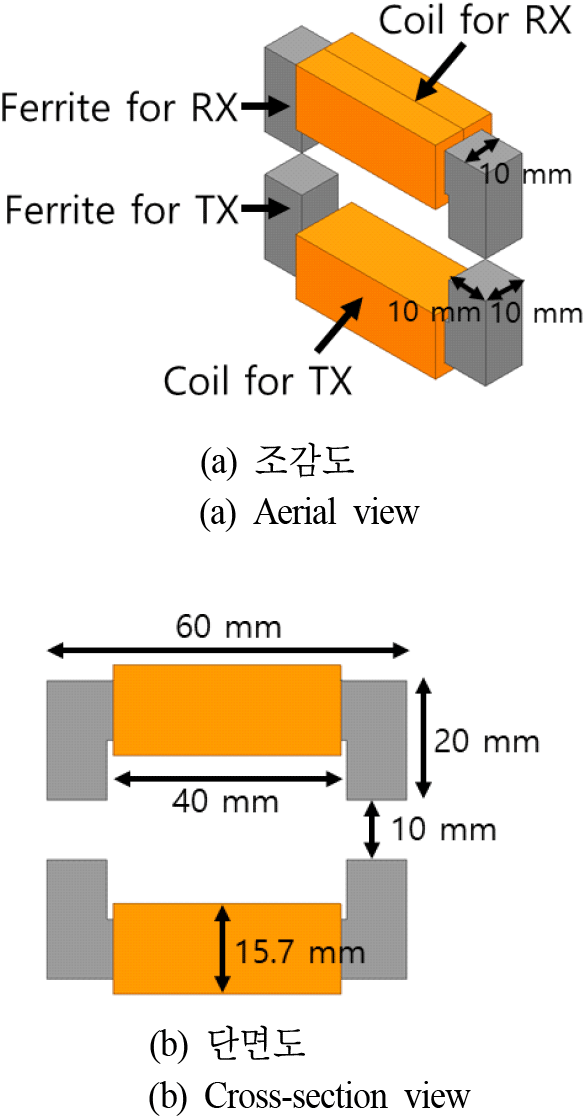
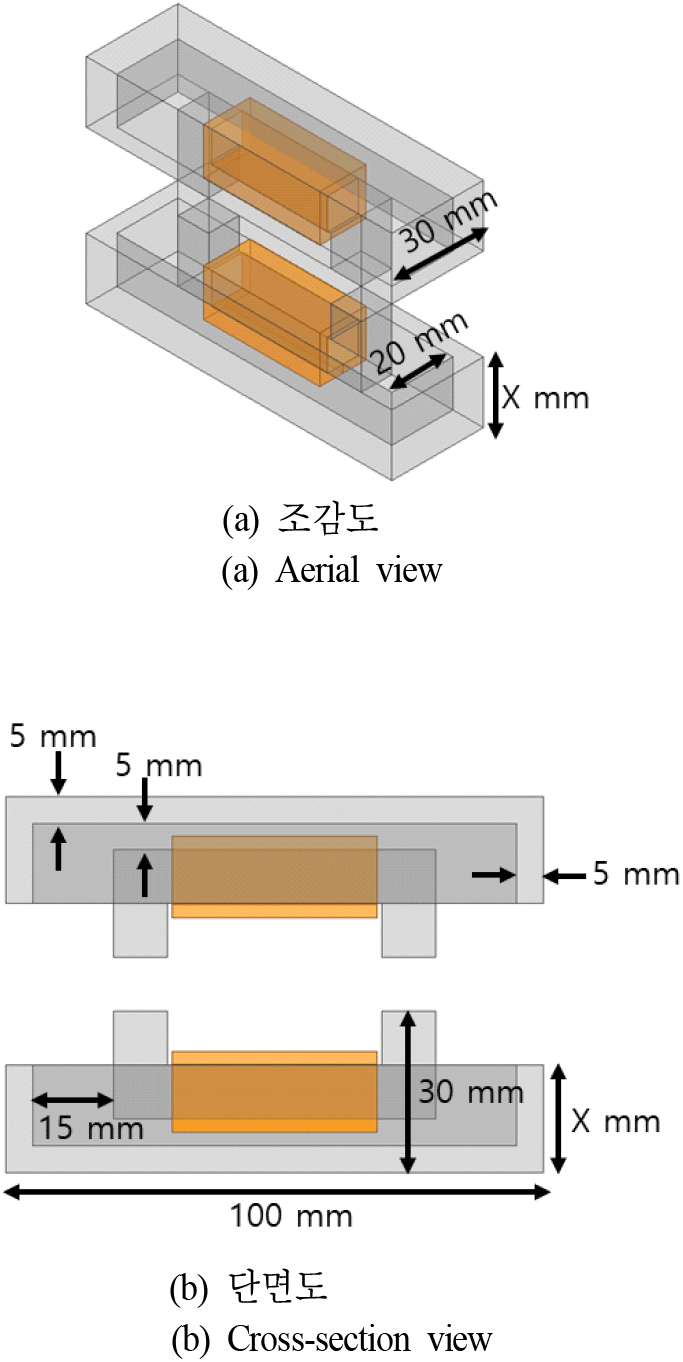
코일, 페라이트 등을 포함한 양극성 커플러 구조는 유한요소법 자기장 시뮬레이션 프로그램인 ANSYS사의 MAXWELL[8]을 통해 설계되었다. 격벽이 존재하지 않는 양극성 커플러의 기본 구조는 그림 6과 같이 설계되었다. 자세한 크기 정보는 그림 6에 나타내었으며, 공극은 10 mm로 시뮬레이션하였다. 또한, 기본 양극성 자기장 커플러 구조의 기본 시뮬레이션 셋업은 표 1에 나타내었다. TX와 RX 커플러의 구조는 동일하다. 한편, 페라이트 격벽이 적용된 양극성 커플러 구조를 시뮬레이션하기 위하여, 그림 7과 같이 페라이트 격벽을 적용한 양극성 커플러 구조를 디자인하였다. 모든 크기 정보는 그림 7에 나타내었으며, 앞서 2장에서 설명된 것과 같이, 격벽의 높이(X mm)를 변화시켜 코일의 자기 인덕턴스와 코일 간의 상호 인덕턴스(결합계수)의 변화를 분석하였다. 페라이트 격벽의 비투자율 또한 표 1에 명시된 것과 같이 3,200 으로 채택하였다.
| Parameters | Value |
| Simulation frequency | 85 kHz |
| Diameter of wire | 2.85 mm |
| Turns of coil | 14 turns, 1 layer |
| Permeability of Ferrite | 3,200 |
표 2는 그림 7의 시뮬레이션 셋업에서 페라이트 격벽 높이(X mm)를 0에서 30 mm까지 10 mm 단위로 변화시켜가며 수행한 자기장 시뮬레이션 결과를 보여준다. 그림 7에서 알 수 있듯이, 격벽의 높이가 0 mm인 경우는 양극성 커플러 외부의 페라이트 격벽을 적용하지 않은 경우를 의미한다. 또한, 30 mm인 경우는 페라이트 격벽의 높이가 커플러를 위한 페라이트 코어의 높이와 같은 경우를 의미한다. 즉, 30 mm 이상의 높이에서는, 공극을 결정하는 커플러의 페라이트의 높이보다 페라이트 격벽의 높이가 더 높아지므로 물리적으로 의미가 없는 결과를 낳는다.
| Height of Ferrite wall (X mm) | Self inductance (TX, RX) (μH) | Mutual inductance (μH) | Coupling coefficient |
|---|---|---|---|
| 0 (Witdout ferrite wall) | 22.1 | 4.76 | 0.215 |
| 10 | 31.6 | 3.9 | 0.123 |
| 20 | 39.4 | 3 | 0.076 |
| 30 | 43.3 | 1.9 | 0.044 |
앞선 자기저항 모델로 해석된 바와 같이, 표 2에서 격벽의 높이가 높아질수록 커플러 페라이트와 격벽 사이의 자기 저항 R1a-1과 R1a-2(혹은 R2b-1과 R2b-2)가 감소하여 코일 스스로 쇄교하는 자속(Λ11 또는 Λ22)이 증가하여, 식 (3)에 의해 자기 인덕턴스가 증가하게 된다. 반면, 상호 인덕턴스는 페라이트 격벽이 높아질수록 커플러에서 발생된 자기장이 점점 더 페라이트 격벽으로 유도되어 자기 인덕턴스가 커지는 동시에, 상대 커플러로 쇄교되는 자기장(Λ12)이 감소하여 식 (4)에 의해 상호 인덕턴스가 감소함을 알 수 있었다. 따라서 페라이트 격벽이 존재하지 않을 때보다 높이가 10 mm일 때 상호 인덕턴스가 감소 하지만, 페라이트 격벽이 10 mm을 초과하여 높아질 때보다는 상호 인덕턴스의 감소가 최소화됨을 표 2에서 알 수 있다.
한편, 마찬가지로 식 (5)에서 알 수 있듯이, 상호 인덕턴스는 감소하며, 자기 인덕턴스는 증가하였으므로 결합계수는 격벽의 높이가 증가함에 따라 감소하는 것을 알 수 있었다.
페라이트 격벽의 높이에 따른 WPT 커플러의 인덕턴스 및 결합계수값을 바탕으로 실제 커플러 주변의 자기장이 감소되었는지의 여부를 시뮬레이션을 통해 알아본다. 공정한 비교를 위하여, 격벽의 높이에 따라 TX 코일의 전류를 달리하여 시뮬레이션을 진행하였다. 본 논문에서는 LCC-series(LCC-S) 토폴로지의 특성[9],[10]을 통해 격벽의 높이에 따른 필요 전류의 값을 계산한 후, 이를 바탕으로 자기장을 시뮬레이션을 통해 자기장을 구하였다.
그림 8은 LCC-S 토폴로지를 가지는 WPT 시스템의 회로도를 나타낸다. LCC-S 토폴로지의 TX 전류는 식 (6)과 같다.
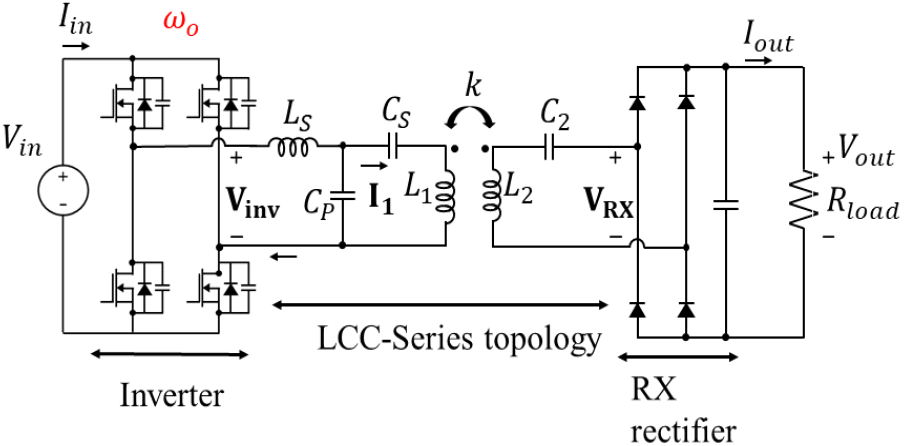
식 (6)에서, I1은 TX 코일에 흐르는 전류이며, CP는 TX 측의 병렬 커패시턴스, Vinv는 인버터의 출력 전압, 그리고 Vin은 인버터의 입력 전압이다. 또한, ω은 인버터의 동작주파수이다. TX 측의 LCC 토폴로지의 특성은 입력 전압이 일정하면 TX 코일에 흐르는 전류가 부하에 관계없이 일정하다는 점이다. 한편, RX 측 정류기 입력에 유도되는 전압인 VRX는 식 (7)과 같다.
즉, LCC-S 토폴로지는 입력 전류에 따라, 정류기 입력의 전압(혹은 정류기 출력 전압)이 달라진다는 것을 알 수 있다.
본 논문에서는 페라이트 격벽의 높이에 따른 공정한 비교를 위하여 표 2의 상호 인덕턴스의 변화에도 불구하고 RX 정류기 입력에 같은 전압이 유도되는 전류로 TX 코일에 흐르는 전류를 채택한다. 즉, 식 (8)과 같이 I1이 구해진다.
식 (8)에서 페라이트 격벽에 관계없이 RX 정류기 출력에 유도되어야 하는 전압(VRX)은 모두 20 V로 선정한다. 페라이트 격벽에 따라 변화하는 상호 인덕턴스를 통해 구해진 TX 전류는 표 3에서 정리되었다. 표 2와 식 (8)에서 알 수 있듯이, 페라이트 격벽의 높이가 증가함에 따라 상호 인덕턴스가 감소한다. 따라서, RX 측에 20 V를 유도하기 위한 전류는 페라이트 격벽의 높이가 증가함에 따라서 증가해야 한다. 한편, RX 코일의 전류는 RX 부하에 같은 전력을 전달하기 위하여 모두 2 A로 선정하였다.
| Height of ferrite wall (X mm) | Target induced voltage of RX rectifier input | TX coil current | RX coil current |
|---|---|---|---|
| 0 (Without ferrite wall) | 20 V | 7.86 A | 2 A |
| 10 | 9.60 A | ||
| 20 | 12.50 A | ||
| 30 | 19.7 A |
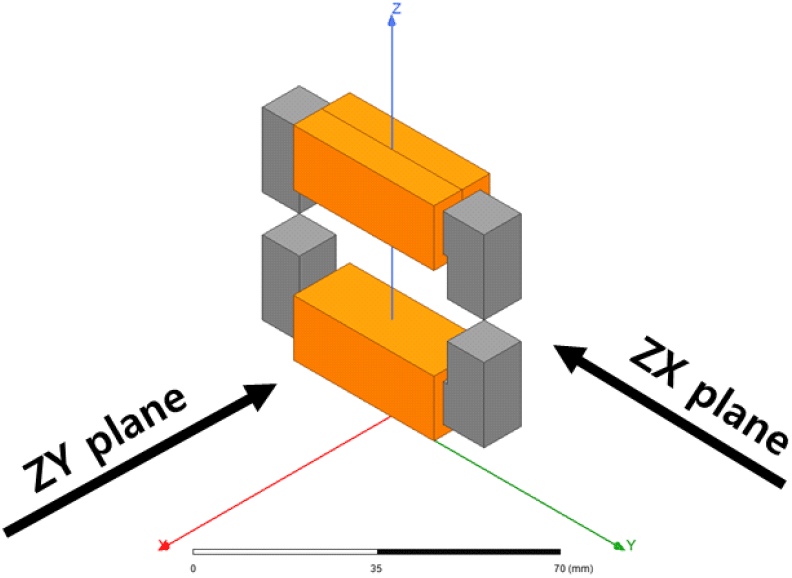
페라이트 격벽의 높이에 따른 누설 자기장 변화를 살펴보기 위하여, 그림 9와 같이 WPT 구조의 누설 자기장을 ZX평면과 ZY평면에서 관찰하였다. 그림 10은 표 3의 전류의 값들을 각 대응하는 페라이트의 격벽 높이를 가지는 자기장 커플러의 코일에 인가하여 주변 자기장 분포를 ZX 평면에서 살펴본 결과이다. 그림 10(a)에서 알 수 있듯이, 자기장 격벽이 존재하지 않으면, WPT를 위한 양극성 커플러 주변으로 자기장이 상대적으로 많이 방사되는 것을 알 수 있었다. 또한 그림 10(b)∼그림 10(d)에서 알 수 있듯이, 페라이트 격벽이 증가할수록 커플러 주변에 방사되는 자기장이 현저히 감소하는 것을 알 수 있었다. 표 3에서와 같이 페라이트 격벽의 높이가 높을수록 TX 코일의 전류를 증가시켰는 데도 불구하고, 전류의 세기와 관계없이 페라이트 격벽의 높이가 높을수록 WPT 자기장 커플러 주변으로 방사되는 자기장의 값이 감소한다는 것을 알 수 있었다.
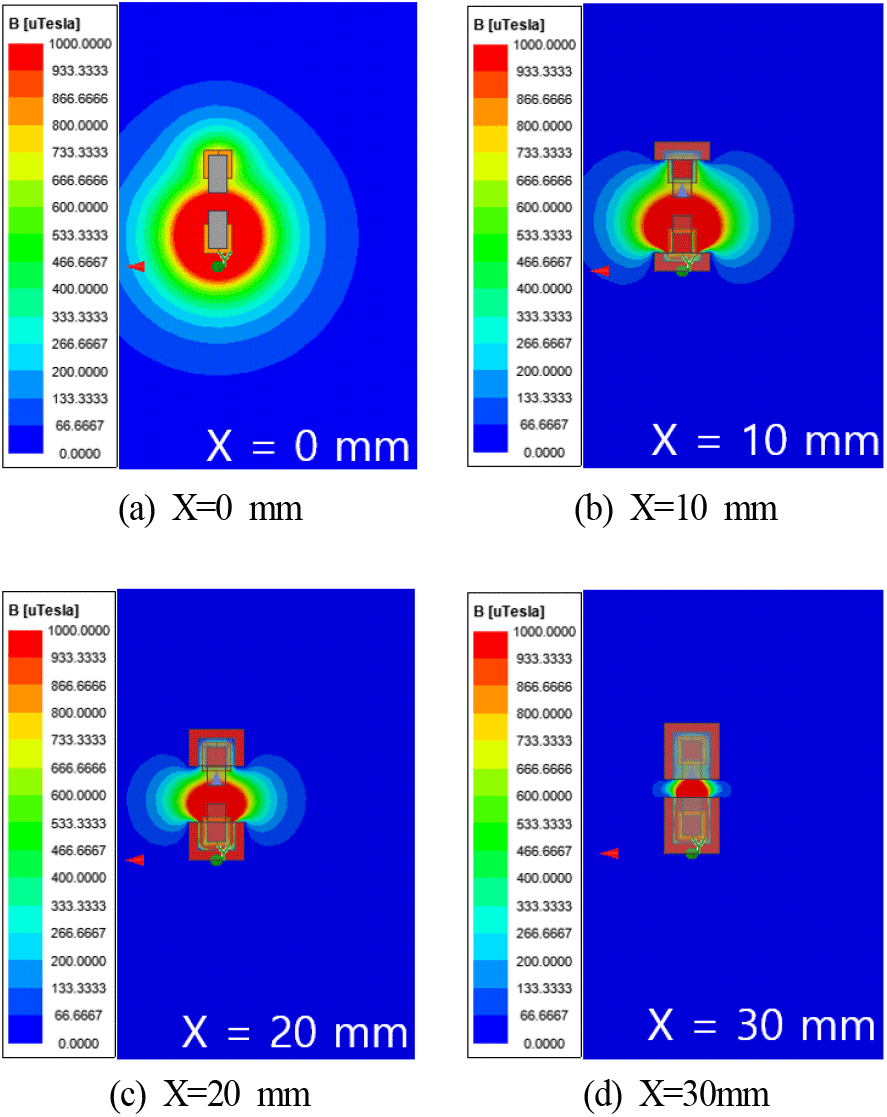
한편, 그림 11은 그림 9의 자기장 관찰시점 중 ZY 평면에서, 자기장 격벽의 높이에 따른 누설 자기장을 살펴본 결과를 보여준다. 그림 10의 ZX 평면과 마찬가지로, 자기장의 격벽의 높이가 증가함에 따라서 누설 자기장은 감소하는 것을 그림 11를 통해 알 수 있다.
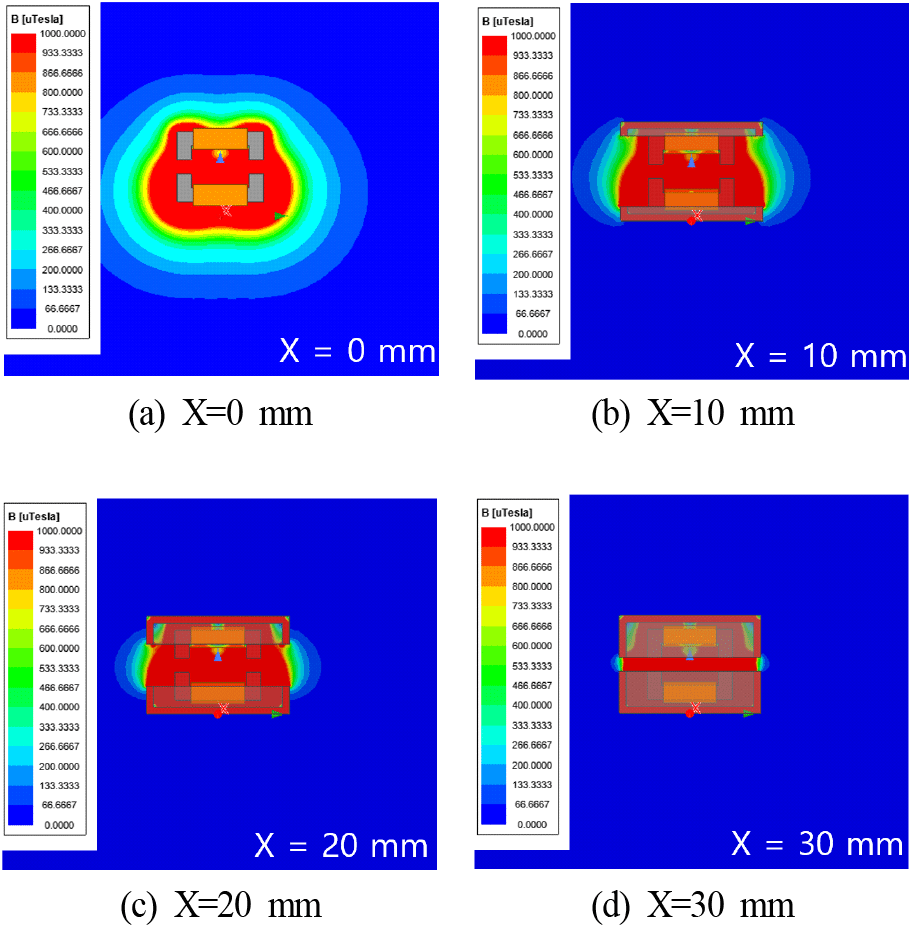
또한, 그림 12는 WPT 커플러의 중앙부터 거리에 따른 자기장의 변화를 보여준다. 그림 12(a)는 측정 지점을 보여주며, 그림 12(b)는 페라이트 격벽의 높이에 따른 자기장의 변화를 보여준다. 표 3과 같이 격벽의 높이가 증가함에 따라 TX 코일의 전류가 증가함에도 불구하고, 그림 12(b)와 같이 거리에 따른 자기장이 격벽이 높을수록 현저히 감소하는 것을 알 수 있다. 또한, 거리 200 mm에서 측정값을 살펴보면, 격벽이 있을 때와 없을 때의 차이가 최소 2.5배에서 20배 이상 차이가 나는 것을 알 수 있다. 따라서 양극성 자기장 커플러에서의 자기장 감소효과는 페라이트의 격벽의 높이보다는 페라이트 격벽의 유무에 더 의존한다는 것을 알 수 있다.
Ⅳ. 실험을 통한 페라이트 격벽 구조 효용성 확인
그림 13은 실제 제작된 페라이트 격벽이 채택된 양극성 커플러 구조를 보여준다. 양극성 커플러는 그림 6의 크기정보와 표 1의 정보를 통해 제작되었다. 교류 저항을 감소시키기 위해 Litz wire를 채택하였다. 또한, 페라이트 격벽의 구조도 함께 제작되었는데, 본 논문의 증명을 위하여 그림 7에서 격벽의 높이가 10 mm(X=10 mm) 인 경우로 제작하였다. 표 4는 실제 제작된 코일의 전기적 파라미터들을 측정한 값이다. 앞선 시뮬레이션에서 예상된바와 같이, 페라이트 격벽이 있을 경우를 페라이트 격벽이 존재하지 않는 경우와 비교하면 자기 인덕턴스는 약 44 % 증가하며, 상호 인덕턴스는 약 15 % 감소한 것을 알 수 있다.

제작된 커플러를 바탕으로 40 W 급 WPT 시스템을 구성하여 페라이트 격벽을 적용하면, 실제로 자기장이 감소하는지 측정하였다. 그림 8과 같이 LCC-S 회로를 구성하였다. LCC-S의 공진 방정식은 식 (9) 및 식 (10)과 같다.
식 (9)는 TX 측의 공진 방정식이며, 식 (10)은 RX 측의 공진 방정식이다. 각 심볼은 그림 8의 회로도에 대응된다. fn1과 fn2는 각각 TX 측과 RX 측의 공진 주파수이며, fo는 인버터의 동작주파수이다.
앞서 표 3과 마찬가지로 공정한 비교를 위하여 페라이트 격벽의 유무에 관계없이 RX 정류기 입력 전압이 동일해야 한다. 페라이트 격벽 유무에 관계없이 RX 정류기 입력 전압이 20 V가 되기 위하여, 식 (8)과 표 4를 통해 구해진 WPT 시스템의 회로값들은 표 5와 같다. 각 회로 소자들이 적용된 최종 실험 셋업은 그림 14와 같다. 모든 전력 측정은 전력분석기와 오실로스코프를 통해 수행하였으며, 자기장 측정은 그림 12와 같이 WPT 커플러에서 200 mm의 거리에서 측정하였다.
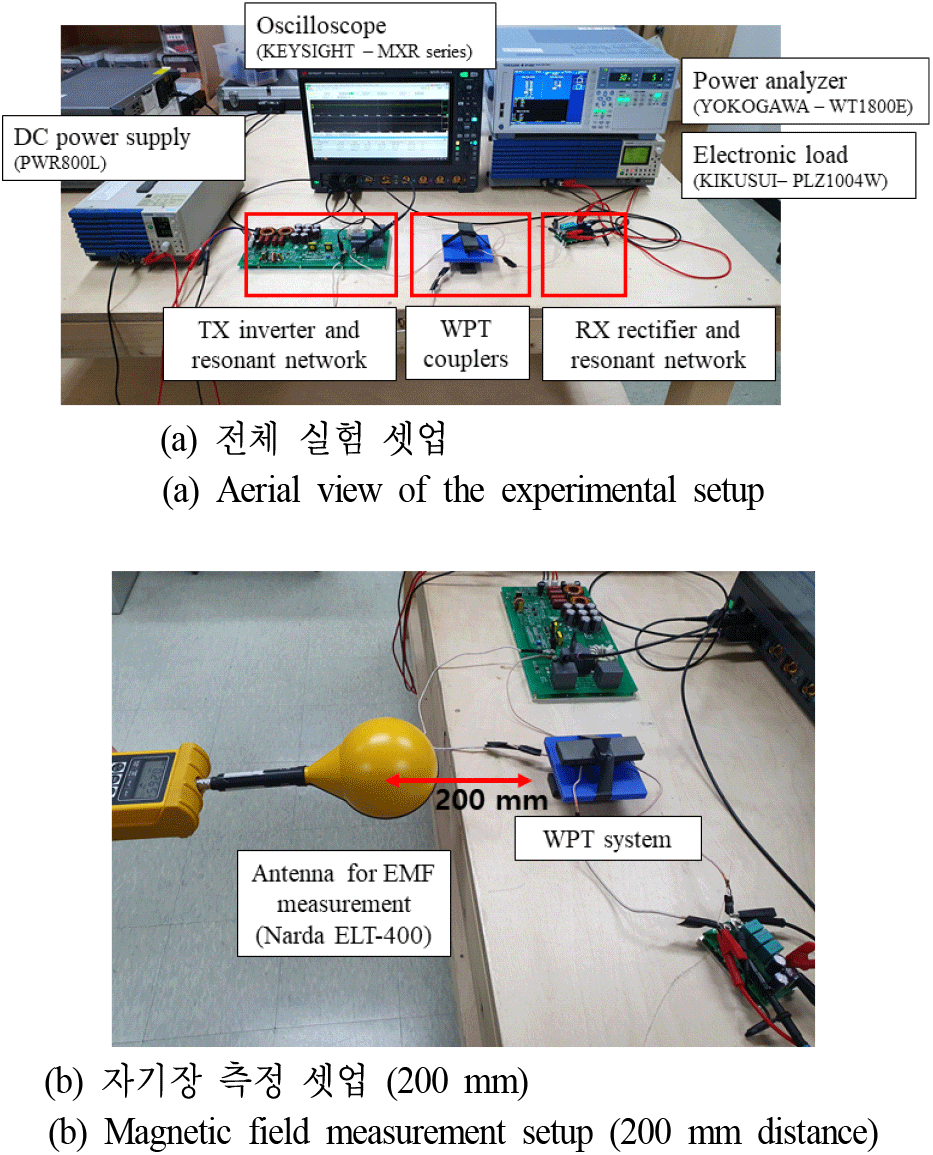
그림 15는 양극성 커플러 구조를 가지는 WPT 시스템에서 페라이트 격벽 유무에 따른 전력전송 효율 변화와 자기장 측정 결과를 나타낸다. 먼저 자기장의 경우, 그림 14(b)와 같이 WPT 자기 커플러에서 200 mm 떨어진 지점에서 측정하였다. 앞서 시뮬레이션에서 예상된 바와 같이 페라이트 격벽이 있을 경우에는 없을 때보다 누설 자기장이 4.12 μT에서 1.68 μT로 약 60 % 가량 감소하였다. 이는 페라이트 격벽 구조가 자기장 감소에 효과가 있다는 것을 보여준다.
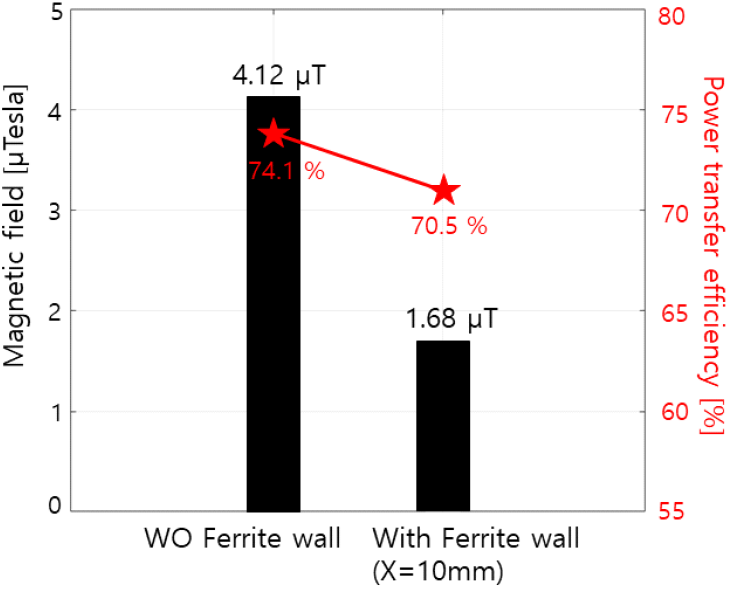
한편, 전력전송 효율은, 그림 8에서 부하에 전달된 DC 출력 전력 Pout(Vout×Iout)을, DC 입력 전력 Pin(Vin×Iin)으로 나눠준 값으로 정의한다. 또한, 모두 40 W의 전력이 전달되었으며, 자세한 전압, 전류, 그리고 전력값은 표 6에 명시되어 있다. 그림 15에서 알 수 있듯이, WPT 시스템들의 전력전송 효율이 74.1 %에서 70.5 %로 3.6 % 감소하였는데, 이는 표 4에서 알 수 있듯이 상호 인덕턴스와 결합계수가 감소하였기 때문이다. 상호 인덕턴스와 결합계수 감소로 인해 표 5와 같이 같은 전압과 전력을 위해서는 전류가 증가하여야 하는데, 이 때문에 전력소모가 증가하였다. 하지만, 3.6 %의 전력 효율 감소로 약 60 %의 누설 자기장 감소가 가능하였다.
양극성 커플러의 누설 자기장을 저감하기 위한 기존 방법[4]에서는 금속 차폐 구조를 채택하였는데, 이는 누설 자기장으로 인한 와전류 손실이 발생하여 효율이 악화되는 등의 단점이 존재하였다. 하지만, 알루미늄 금속 대신 페라이트 격벽 구조를 사용하게 되면 와전류 손실이 발생하지 않아서 효율 감소는 최소화되면서도, 자기장을 효과적으로 차폐할 수 있어서 그 효용성이 매우 크다.
Ⅴ. 결 론
본 논문에서는 WPT 시스템의 양극성 커플러의 누설 자기장의 감소를 위한 페라이트 격벽 구조를 제안하였다. 페라이트 격벽을 적용하면, WPT 시스템의 자기장이 페라이트 격벽으로 유도되어 누설자기장이 감소하게 된다. 하지만, TX 코일에서 RX 코일로 전달되어야 하는 자기장도 함께 페라이트 격벽으로 유도되기 때문에, TX와 RX 코일 간의 결합계수와 상호 인덕턴스가 감소하는 문제점이 발생한다.
본 논문에서는 페라이트 격벽의 높이를 조절하여, 누설 자기장은 감소하면서도 상호 인덕턴스의 감소를 최소화할 수 있는 구조를 자기회로 분석과 시뮬레이션을 통해 설계하였다. 페라이트 격벽의 높이가 증가함에 따라, RX 측에 전달되기 동등한 전압이 전달되기 위한 TX 전류가 증가하게 된다. 그럼에도 불구하고, 페라이트 격벽의 높이가 증가할수록 누설되는 자기장이 현저히 감소하게 된다는 것이 시뮬레이션을 통해 증명되었다. 상호 인덕턴스의 감소가 최소화되면서, 누설 자기장의 감소가 가능한 10 mm의 격벽을 제작하여 페라이트 격벽이 있을 때와 없을 때의 누설 자기장과 전력전달 효율을 측정하였다. 페라이트 격벽이 있을 때는 페라이트 격벽이 없을 때보다 자기장은 60 % 이상 감소하면서, 전력전송 효율은 3.6 % 감소한다는 것이 실험을 통해 증명되었다.
따라서, 제안된 페라이트 격벽 구조는 양극성 커플러의 누설자기장 문제를 위해 사용되었던 기존의 알루미늄 차폐구조에 비해 효율 감소는 최소화되면서, 동시에 자기장의 차폐는 효과적으로 가능하다는 것이 증명되었다.


