논문/REGULAR PAPERS
다중 주파수를 이용한 다수 표적분포의 중심각 추정
Centroid Angle Estimation for Multiple Unresolved Targets Using Frequency Diversity
Joonwoo Bae
1
, Dongmin Park
1
, Joohwan Chun
*,†
*School of Electronic Engineering, KAIST
© Copyright 2021 The Korean Institute of Electromagnetic Engineering and Science. This is an Open-Access article distributed under the terms of the
Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits
unrestricted non-commercial use, distribution, and reproduction in any
medium, provided the original work is properly cited.
Received: May 03, 2021; Revised: May 26, 2021; Accepted: Jul 07, 2021
Published Online: Jun 30, 2021
요약
근접방어 무기체계(closed-in-weapon system: CIWS) 운용에는 발사되는 아군 대응탄들(bullets)의 중심점이 원하는 방향을 향하도록 포신을 정렬하는 사전정렬(pre-action calibration) 작업이 필요하다. 이를 위하여는 우선 대응탄들의 중심점 각도를 추정하여야 하는데, 본 논문에서는 모노펄스 방식의 추적 레이다에 있어서 사전정렬시에 다중주파수를 사용하면 중심점의 각도 추정 정확도가 단일주파수를 사용할 때보다 크게 향상됨을 보였다.
Abstract
Successful operation of a closed-in weapon system (CIWS) requires pre-action calibration that aligns the axis of a gun barrel such that the centroid angle of the outgoing friendly bullets coincides with the desired direction. However, the pre-action calibration in turn requires an accurate centroid angle estimate. This study demonstrates that the accuracy of the centroid angle estimation with monopulse tracking radar improves greatly by adopting a frequency diversity technique.
Keywords: Centroid Angle Estimation; Unresolved Targets; Monopulse Radar; CIWS
Ⅰ. 서 론
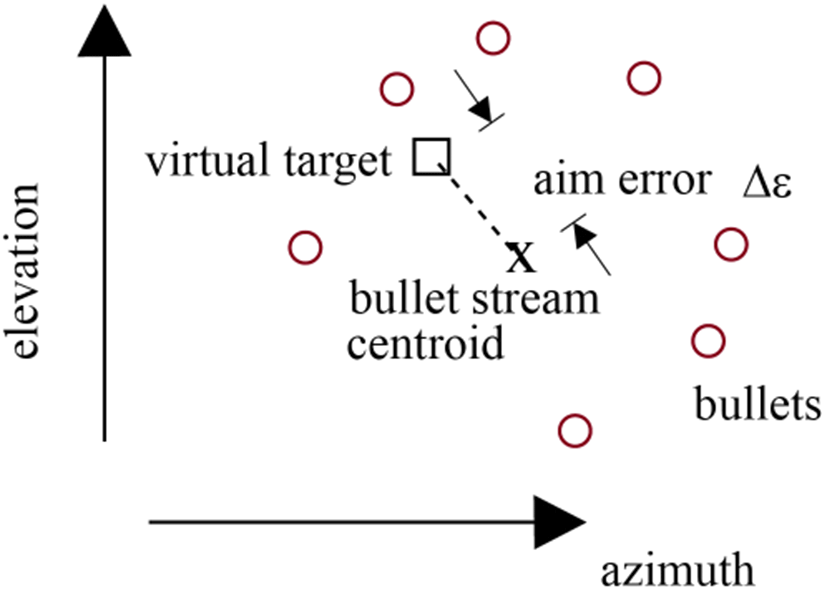
한 개의 분해영역(resolution cell) 안에 여러 개의 미분해(unresolved) 표적들이 존재할 때 이들 표적의 중심점(centroid)의 각도(elevation, azimuth angles)를 찾는 문제는 근접방어 무기체계(closed-in-weapon system: CIWS) 운용에 필요하다(여기서 분해영역이란 양자화된 거리 혹은 도플러가 다른 값을 갖는 셀을 의미한다). 즉 사전에 가상표적을 향하여 실제로 대응탄들(bullets)을 2-3초간 발사한 후 대응탄들의 중심점의 각도(중심각)가 가상표적의 각도와 일치하도록 포신을 정렬(gun laying)하여야 한다[2],[3]. 이와 같은 사전정렬(pre-action calibration)에는 모노펄스 추적레이다를 이용하여 대응탄들의 중심각을 정확히 추정하는 작업이 필요하다. 그림 1에 가상표적의 각도, 같은 분해영역 안에 존재하는 대응탄들의 각도 및 대응탄들의 중심각을 각각 네모, 원 및 “x”로 표시하였다. 사전정렬 수행 후에는 조준오차(aimi error)가 0이 된다(Δϵ = 0).
그림 1. | Fig. 1.
대응탄각도(‘o’), 대응탄중심(‘x’)과 가상표적(‘□’)의 각도. 조준오차 = |‘□’-‘x’| | Angles of bullets(circle), bullet centroid(cross) and virtual target(square). aim error=|square-cross|.
Download Original Figure
모노펄스 방식을 사용하면 한 개의 분해영역 안에 존재하는 단일표적의 각도를 추정할 수 있다. 한 개의 분해영역 안에 두 개 이상 다수의 표적이 존재할 경우는 각각 표적들의 각도를 찾아서 이들 각도의 평균을 계산하여 중심각을 얻을 수 있다. 이때 표적 각각의 각도를 찾는 작업은 일반적인 모노펄스 방식으로는 불가능하고, MLE (maximum likelihood estimator) 등, 많은 계산량이 필요한 다중안테나 신호처리 기법을 사용하여야 한다[4],[5].
하지만 한 개의 분해영역 안에 두 개 이상 다수의 표적이 존재할 경우에 모노펄스 기법을 사용하여(한 개의) 각도를 구하면 평균적으로 다수표적의 중심각을 준다는 사실이 알려져 있어서[1], 굳이 계산량이 많은 다중안테나 신호처리 기법을 사용하지 않고도 모노펄스 추적레이다로 근접방어시스템의 사전정렬을 수행할 수 있다.
본 논문에서는 모노펄스를 이용한 중심각 추정에 있어서 다중주파수를 사용하여 평균을 취하면 단일 주파수를 사용하여 평균을 취한 경우보다 중심각 추정이 정확함을 모의실험을 통하여 보였다.
Ⅱ. 모노펄스를 이용한 중심각 추정
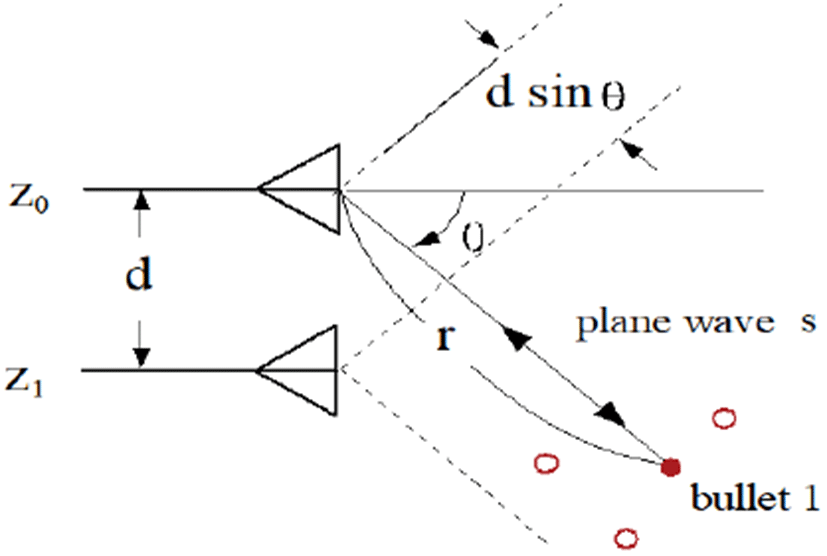
모노펄스 원리는 그림 2로 설명할 수 있다. 간격이 d인 두 개의 안테나로 얻은, 붉은 점(solid circle)으로 표시된 한 개의 대응탄에 의한, 잡음이 없는 측정값을 각각 z0=1, z1=eju라고 하자. 여기서 u=kdsinθ, k=2π/λ 이다. 이때 합/차 신호를 각각 Σ=z0+z1,Δ=z0-z1라고 하면, 모노펄스비 A는 식 (1)과 같이 정의된다[6].
식 (1)에서 A는 순허수, 즉 Im(A)=−tan(u/2) 임을 알 수 있다. 그러므로 식 (1)을 u에 대하여 풀면
와 같이 되고, 측정한 z0, z1로부터 식 (2)를 이용하여 한 개의 대응탄의 각도 θ를 얻을 수 있다. 측정치 z0, z1에 잡음이 있을 경우, 위 식 (2)로 얻은 각도는 근사적으로 MLE임이 알려져 있다[7].
만약 그림 2에 보인 바와 같이 다수의 대응탄들(붉은 점 및 붉은 원)이 존재할 경우에 z0, z1를 구하여 식 (2)로부터 각도 θ를 구하면 이 각도는 대응탄들의 중심각이 됨이 알려져 있다[1]. 이 경우 물론 모노펄스 비 A는 순허수가 아니고, 실수부도 가지게 되며, |Re(A)|를 이용하여 두 개 이상의 표적이 존재하는지 판별하는 방법도 연구되었다[6].
본 논문이 새롭게 기여하는 바는 다음과 같다.
-
다수표적의 경우, |Re(A)|를 이용하여 추정한 중심각의 정확도를 판별할 수 있음을 모의실험으로 보였다.
-
다수표적에 대하여 식 (2)를 사용하여 중심각을 구할 경우, z0, z1의 위상은 각도뿐만 아니라, 거리에 따라서도 바뀌므로 신호모델에 거리도 고려하여야 함을 인식하고,
-
이 경우, 대응탄들이 같은 각도분포를 가짐에도 사용하는 주파수에 따라 z0, z1의 위상이 바뀌는 효과에 의하여 식 (2)에 의한 중심각 추정이 보다 정확하여짐을 모의실험을 통하여 보였다.
이제 대응탄 m까지 거리가 rm이고, 거리변화율이 이라고 하자. 또한 하나의 burst안에 N개의 펄스가 있고, PRI(pulse repetition interval)가 T라고 하면 펄스 n일 때 대응탄 m 까지의 거리는
로 주어진다. 여기서 r0m는 펄스 1일 때 대응탄 m까지 거리이다. 또한 매 펄스마다 주파수가 Δf씩 증가한다면 n 번째 펄스 때 수신신호 위상은
가 되고 대응탄 m에 대한 두 안테나의 측정값은
가 된다. 그러므로 M개 전체 대응탄에 대한 두 안테나의 측정값은 다음과 같다.
여기서 위의 변수들은 다음과 같이 정의된다.
그러므로 식 (6)을 이용하여 두 안테나에서 측정값 z0, z1을 모사하고, 식 (2)로 중심각을 추정한다.
Ⅲ. 모의실험 결과
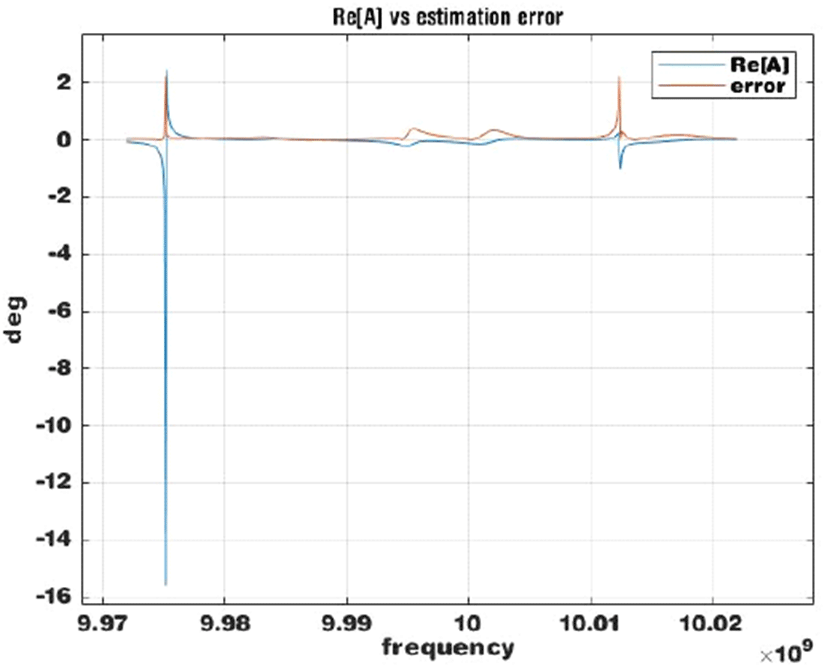
그림 3은 M=4, Δ f=0의 경우, 측정잡음이 없을 때 중심각 추정오차를 송신 주파수 f0 에 대하여 그린 그래 프이다. 사용한 파라메터는 표 1과 같다. 여기서 표적까지의 거리 r은 상대값만 위상에 영향을 주므로 편의상 작은 값을 사용하였다. 그림 3에서 추정오차(error)는 주파수 f0 (Δ f = 0)에 따라 변하는데, 그 이유는 위상 φm이 주파수의 함수이기 때문이다. 또한 추정오차가 클때 |Re(A)|도 큰 값을 가지므로 Re(A)를 추정 정확도를 알려주는 표지(indicator)로 사용할 수 있다.
그림 4∼그림 7은 1,000번의 시행으로 얻은 결과이고, 사용한 파라메터는 표 2와 같다. 여기서 U[a, b]는 a,b사이 균일(uniform) 확률분포를 의미한다.
표 2. | Table 2.
그림 4∼그림 7에서 사용한 파라메터 | Parameters used for Figs 4∼7.
|
f0[GHz] |
d[λ] |
r[m] |
θ[deg] |
M
|
|
10 |
8 |
U(−10,10) |
U(−2.9,2.9) |
4 |
|
Fig |
N
|
Δf[MHz] |
SNR[dB] |
[m/sec] |
|
4 |
16 |
0 or 10 |
−10~30 |
1,100 |
|
5 |
16 |
0 or 10 |
−10~30 |
U(1090,1110) |
|
6 |
1~130 |
0 or 150/N |
20 |
1,100 |
|
7 |
1~130 |
0 or 150/N |
20 |
U(1090,1110) |
Download Excel Table
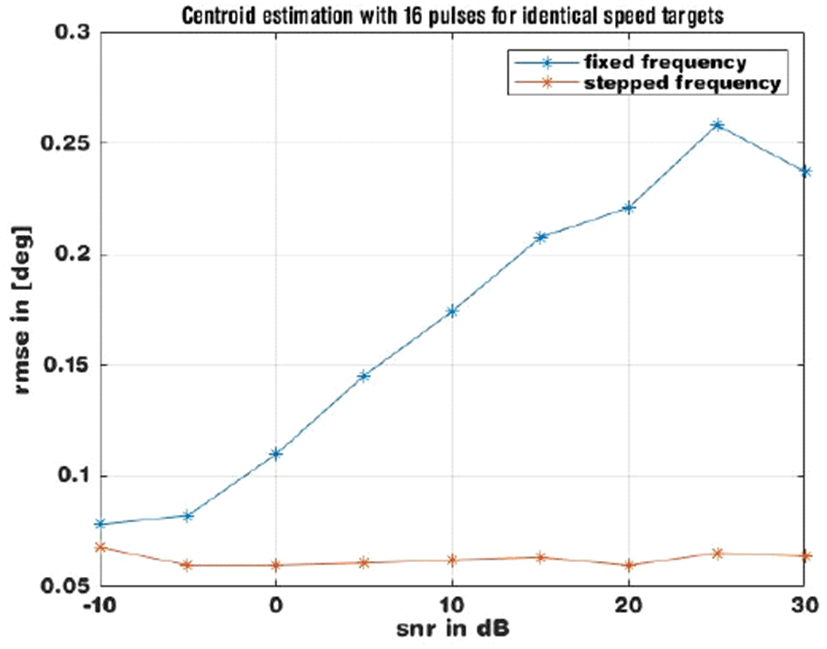
그림 4는 동일한 속도의 대응탄들에 대하여 동일한 주파수와 다중 주파수를 사용하였을 때 추정한 중심각의 root mean squared error(RMSE) 값을 signal-to-noise(SNR)
에 대하여 도시한 그래프이다. 동일한 주파수의 경우, SNR이 높아지면 오히려 오차가 커지는 경향이 있다.
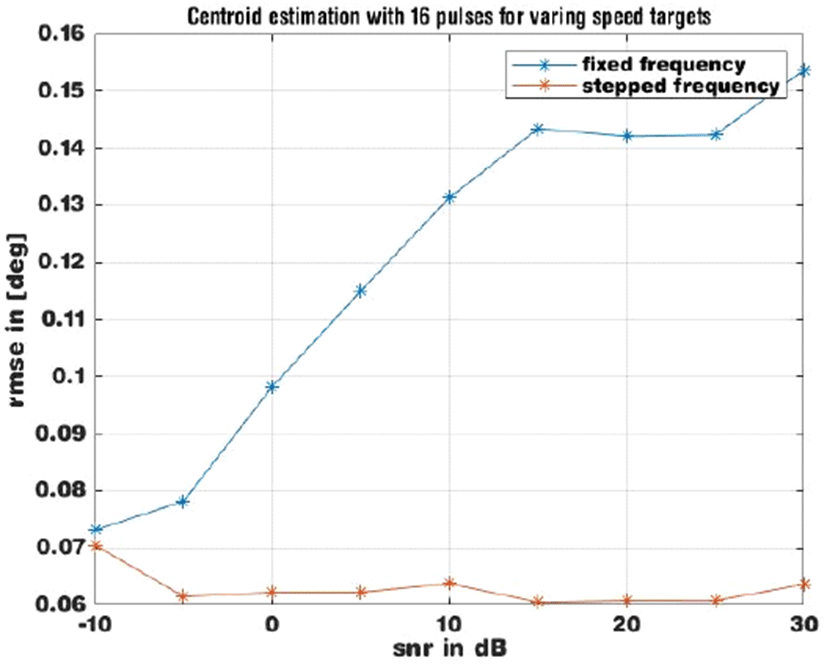
그림 5에 대응탄들이 다른 속도를 가질 경우, 추정한 중심각의 RMSE를 SNR에 따라 도시하였다. 그림 4와 비교하여 특히 동일한 주파수의 경우, 오차가 줄어 듦을 알 수 있다.
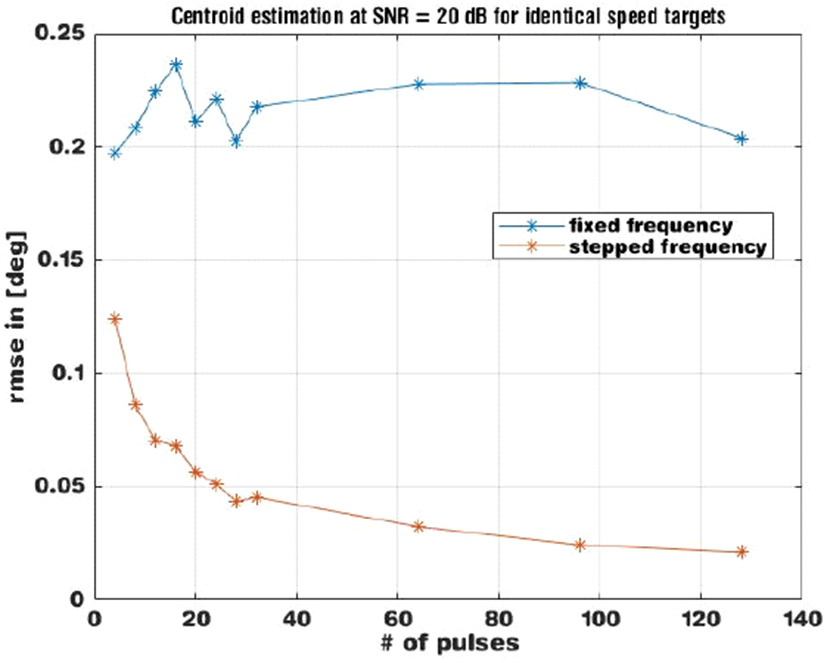
그림 6은 대응탄들이 같은 속도를 가질 경우, 동일한 주파수와 다중 주파수를 사용하였을 때 추정한 중심각의 RMSE를 펄스 개수에 따라 비교한 그래프이다. 펄스개수가 많아질 때, 다중 주파수를 사용하면 오차가 줄어들지만, 동일한 주파수를 사용하면 오차에 변화가 없음을 알 수 있다. 공평한 비교를 위하여 전체 대역폭을 동일하게 150 MHz로 두었다.
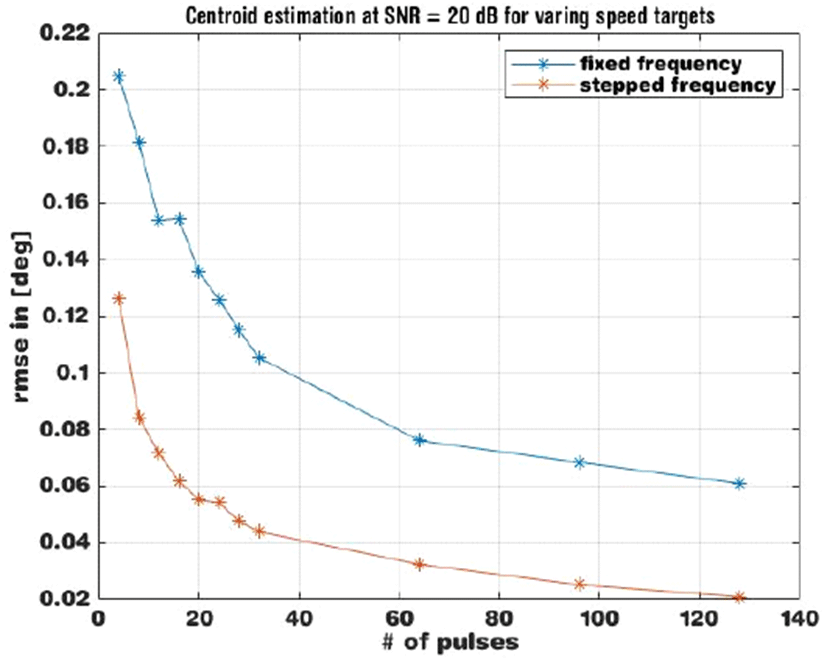
그림 7은 대응탄의 속도가 다를 경우, 추정한 중심각의 RMSE값을 보였다. 펄스개수가 많아지면 동일 주파수, 다중주파수 모두 오차가 작아진다.
Ⅳ. 결 론
모노펄스를 이용한 다수표적의 중심각 추정에 있어서 다중주파수를 사용하면 추정각도의 RMSE가 크게 줄어드는 것을 모의실험을 통하여 보였다. 본 결과는 CIWS 포의 사전정렬에 사용할 수 있다.
Acknowledgements
본 연구는 한화시스템의 지원으로 수행된 연구임.
References
G. Gordon, “Monopulse estimation of the centroid of an ensemble of radar scatterers,”
IEEE Transactions on Aerospace and Electronic Systems, vol. AES-11, no. 1, pp. 94-102, Jan. 1975.


D. Serakos,
Phalanx CIWS Control System Stability,
Aim Bias Compensation,
and Noise Sensitivity, Dahlgren, VA, NSWC, 1992.


J. Peterschmidt,
Normal Modes of Vibration of the Phalanx Gun, Monterey, CA, Naval Postgraduate School, 1993.

Y. Oh, J. Chun, J. Suh, J. Jung, J. Kim, and J. Lee “Multipath angle estimation for low-flying target of multi-frequency shipborne radar,”
SPIE Future Sensing Technologies, vol. 11197, p. 111970C, Nov. 2019.


D. Park, E. Yang, S. Ahn, and J. Chun, “Adaptive beamforming for low-angle target tracking under multipath interference,”
IEEE Transactions on Aerospace and Electronic Systems, vol. 50, no. 4, pp. 2564-2577, Oct. 2014.


S. Sherman,
Monopulse Principles and Techniques, Boston, MA, Artech House, 1984.

U. Nickel, “Overview of generalized monopulse estimation,”
IEEE Transactions on Aerospace and Electronic Systems Magazine, vol. 21, no. 6, pp. 27-56, 2006.