Ⅰ. 서 론
레이다(radar)는 원활한 표적 정보 획득을 위해 능동위상배열레이다의 전기적 빔조향 특성을 이용한 빔그리드를 형성하여 전방위각/고각에 대해 표적을 탐색할 수 있다. 레이다는 한정된 시간 내에 효과적인 임무 수행을 위해 광역빔을 이용하며, 광역빔은 각 안테나 소자의 크기나 위상을 조정하여 설계한다[1],[2].
광역빔 패턴을 최적화하기 위한 방법으로는 여러 가지 알고리즘이 연구되어 왔다. 우선 휴리스틱 알고리즘으로 유전알고리즘(genetic algorithm)[3], 입자 군집 최적화(particle swarm optimization)[4] 등이 이에 속한다. 이 알고리즘은 무작위적인 탐색을 기반으로 최적해를 찾으며, 특히 해공간이 복잡하고 조정가능한 변수가 많은 빔패턴 최적화 문제에 주로 사용되어 왔다[5]. 하지만 휴리스틱 알고리즘은 무작위성을 기반으로 해를 찾아가기 때문에 많은 시행착오가 필요해 계산시간이 많이 걸린다. 또한 실제 구한 최적해가 전역적 최적해가 아니라, 국지적 최적해일 가능성도 있으며, 이를 판단하기도 어렵다. 이러한 단점을 극복하기 위해 결정론적 알고리즘이 등장하였다. 이 알고리즘은 주어진 문제를 수식화하여 무작위성을 최소화하여 효과적으로 최적화를 수행하는 방법이다. MVDR(minimum variance distortionless response), DLM(diagonal loading method) 등의 빔패턴 최적화에 대한 가능성을 증명했다[4]. 또한 결정론적 알고리즘 중 하나인 convex 최적화 방법은 convex 집합과 convex 함수를 모두 만족하는 경우에 한해 빔패턴 최적화 연구를 수행해왔다[6]. Convex 최적화 방법을 적용한 빔 패턴 최적화 문제의 경우, 일반적으로 주엽 및 부엽레벨의 상한 마스킹을 적용하는 경우에만 사용할 수 있다. 하지만 이런 방식으로 최적화를 수행하게 되면 광역빔의 주엽 부분에 리플이 크게 생겨 원하는 전력을 일정하게 방사하지 못하는 단점이 있다. 이러한 문제를 풀기 위해서는 주엽레벨의 하한 경계 마스킹을 통해 최적화를 수행해야 하지만, 이는 non-convex 문제이기 때문에 convex 최적화 알고리즘을 그대로 적용하기 어렵다.
이에 본 논문에서는 이러한 단점들을 극복하기 위해서 완전디지털 능동위상배열레이다의 광역빔 패턴 최적화를 위한 위상조정 convex 알고리즘을 제안한다. 먼저 SDR(semidefinite relaxation) 개념을 적용하여 제한조건을 완화시켜 non-convex 집합을 convex 집합으로 전환한다[7]. 또한 배열소자의 크기는 고정하고 위상만을 조정하도록 제한조건을 적용하고, 고유값 분해를 통해 획득한 고유값의 합을 최소화하도록 최적화 과정을 수행한다. 위상조정 convex 알고리즘을 이용한 광역빔 설계 결과와 기존 휴리스틱한 방법으로 설계된 패턴과의 비교를 통해 성능을 확인한다. Ⅱ절에서는 광역빔 설계 개요, Ⅲ절에서는 위상조정 convex 최적화 방법을 다룬다. Ⅳ절에서는 제안된 알고리즘을 이용한 광역빔 설계의 성능을 검증 및 분석한다. Ⅴ절에서는 본 논문의 결론을 맺는다.
Ⅱ. 광역빔 설계 개요
레이다는 임무에 따라 주어진 안테나 개구면 크기를 기준으로 하여 빔을 형성하여 운용한다. 일반적으로 안테나의 크기가 정해지면 레이다 운용빔의 빔폭은 정해진다. 하지만 한정된 시간 하에 효과적인 임무수행을 위해서는 빔폭을 가변하여 운용하는 것이 필수적이다. 광역빔을 설계하기 위해 초기에는 개구면 바깥의 소자의 크기를 강제로 0으로 설정하여 실 개구면 크기를 축소하는 효과를 내거나, 안테나 소자에 크기 테이퍼링을 적용하는 방법을 이용하였다. 하지만 이 방법들은 송신출력이 감소하는 큰 단점이 있다. 이를 극복하기 위해 안테나 소자의 위상만을 조정하여 광역빔을 설계하는 방법이 제안되었다. 하지만, 제한된 bit 양자화 아날로그/디지털 위상변위기를 이용하여, 불연속적인 위상값만을 이용하기 때문에 실제 적용이 어려웠다.
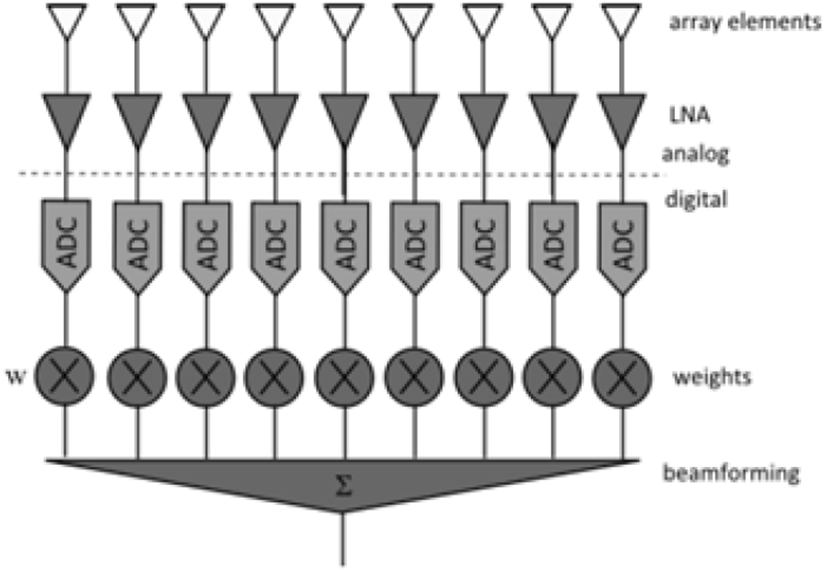
완전 디지털 능동배열레이다는 완전 디지털 빔형성 방식을 이용하여 기존의 아날로그 방식의 변위기를 이용한 아날로그 빔형성 방식, 디지털 변위기를 이용하고 부배열 개념을 적용한 디지털 빔형성 방식보다 많은 장점을 가지고 있다[8]. 완전 디지털 능동배열레이다는 그림 1과 같이 소자 단위로 디지털 단에서 광역빔을 형성할 수 있어, 소자의 크기와 위상을 bit 양자화 에러없이 원하는 대로 설정할 수 있다는 큰 장점이 있다. 즉, 기존에 불연속적인 위상값만으로 패턴을 형성하여 광역빔 설계에 한계가 있었다면, 디지털 단에서 자유롭게 위상 설정을 통해 광역빔 설계가 가능하다.
Ⅲ. 위상조정 Convex 최적화 알고리즘
Convex 최적화 알고리즘을 이해하기 위해서는 convex 집합과 convex 함수 개념을 이해해야 한다[9]. Convex 집합의 정의는 식 (1)과 같으며, 이는 convex 최적화 문제를 정의할 때, 제한조건에 들어가는 명제의 필요조건이 된다.
정확히는 C라는 영역이 convex 집합인지에 대한 명제이다. 이를 기하학적으로 설명하면 C영역 위의 두 점 x1, x2을 선택하여 그 두 점을 일직선으로 이은 선이 존재할 때, 그 선 위의 모든 점은 α로 표현할 수 있고, 이 모든 점은 C 영역 위에 있다는 의미이다. 이를 만족할 때 영역 C는 ‘convex 집합’이라고 일컬을 수 있고, convex 최적화 문제의 제한조건으로 사용할 수 있는 영역이 된다. 반대로 위의 명제를 만족하지 못하는 영역을 ‘non-convex 집합’이라고 일컫고, convex 최적화 문제에서 사용할 수 없는 영역이다.
Convex 최적화 알고리즘 적용을 위해서는 convex 함수의 조건도 만족하여야 한다. Convex 함수는 convex 최적화 문제가 최소값을 찾는 함수, 즉 목적함수가 된다. Convex 함수의 조건 명제는 식 (2)와 같다.
이 명제를 설명하면, 먼저 임의의 벡터 두 개를 정하고, 그 두 벡터를 함수 f에 대입한 함수값을 구한다. 그리고 해당 벡터와 함수값을 갖는 점 x1, x2을 일직선으로 연결하였을 때, 일직선상 위의 모든 점은 해당 범위에서 함수 f에 대입한 함수값들보다 모두 크다는 의미이다. Convex 최적화 알고리즘의 기본적인 형태는 식 (3)과 같다.
f(x)를 최소화시키는 x를 찾되, x가 영역 C에는 포함되어야 한다는 제한조건을 가지는 최적화 문제 형태이다. C는 위에서 언급한 convex 집합이어야 하며, 함수 f(x) 역시 convex 함수이어야 convex 최적화 문제 조건이 갖추어진다. 이러한 조건을 만족시켰을 때, convex 최적화 문제의 특징이 주어지는데, 먼저 ‘국지적 최적해(local optima)가 전역적 최적해(global optima)와 같다’는 것이다. 서론에서 언급하였듯이 휴리스틱 알고리즘의 큰 단점이 바로 국지적 최적해를 찾았을 때, 그것이 전역적 최적해가 아닌 경우가 많다는 것이다. 전체 해 영역 안에 여러 개의 국지적 해가 존재하고, 그중에서 가장 적합한 국지적 해, 즉 전역적 최적해를 선별하는 것은 쉽지 않다. 하지만 convex 최적화 알고리즘은 convex 함수의 특징으로 인해 국지적 최적해가 곧 전역적 최적해가 되는 큰 장점이 있다.
광역빔을 최적화하기 위한 제한 조건은 일반적으로 광역빔 주엽레벨의 크기와 빔폭, 그리고 부엽레벨의 크기이다. Convex 최적화 알고리즘에 적용하기 위한 기본적인 형태는 식 (4)와 같다.
minimize x
조건 1: 주엽레벨 크기=0 dB
조건 2: 주엽레벨 빔폭=5도
조건 3: 부엽레벨≤α
이 조건으로 최적화를 수행하면 주엽레벨의 하한 마스킹이 없기 때문에 convex 최적화 알고리즘을 적용하여도 원하는 광역빔 패턴을 획득할 수 없다. 주엽이 비교적 편평한 패턴을 획득하기 위해서는 추가적인 조건 4가 필요하다.
조건 4: 주엽레벨≥-1 dB
하지만 식 (5)에서 조건 4는 non-convex 집합으로 convex 알고리즘을 적용할 수 없다. Convex 최적화 알고리즘을 적용하기 위해서는 convex 집합, convex 함수를 만족해야 하지만 광역빔 패턴 최적화의 경우, 이를 해결하기 어렵다. 즉, 이를 해결하기 위해서는 non-convex 집합을 convex 집합으로 변경하는 것이 필요하다.
원하는 최적빔을 합성하는 문제에 convex 알고리즘을 적용하기 위해 능동위상배열 레이다의 안테나 배열 원전계 패턴을 다음과 같이 정의할 수 있다.
aH (θ)는 빔형성 허미션(hermition) 행렬신호이며, w는 각 소자별 크기와 위상으로 이루어진 벡터신호이다. fi = f(θ), ai=a(θi)라 정의하고, 식 (6)의 실수 부분을 재계산하면 식 (7)과 같이 표현된다.
T는 transpose 연산자이며, ℝ, 는 각각 실수, 허수를 표 현하는 연산자이다. 능동위상배열레이다의 원전계 방사 전력은 |fi|2와 같이 표현할 수 있으며, Qi는 대칭 행렬이기 때문에 식 (8)과 같이 표현된다.
Tr은 행렬의 대각 계수의 합을 의미하며 방사전력값 자체가 0보다 큰 양수값을 가지므로 X는 대칭 positive semidefinite 행렬이라고 볼 수 있다. 이때, X로부터 x를 구하기 위한 조건은 X는 0보다 같거나 크고, X의 랭크는 1이라는 조건을 만족할 때, 배열소자의 크기/위상 분포인 x를 구할 수 있다.
위 식들을 정리하여 배열소자의 크기/위상 분포를 구하기 위한 최적화 식을 정의하면 식 (9)와 같다.
위 식은 X가 0을 포함하고 있어, semidefinite 행렬이며, 랭크 제한조건이 들어있어 non-convex 문제이다. 랭크 제한조건을 완화(relaxation)하면 convex 최적화 문제로 변환이 가능하며, 이렇게 convex 문제로 변환하는 방법을 SDR (semidefinite relaxation)이라 한다[7].
식 (10)에서 랭크 조건을 삭제하였지만, X를 전역적 최적해로 구하기 위해서는 최대한 랭크를 최소화해야 한다. 랭크를 최소화하기 위한 대표적인 휴리스틱한 방법으로는 X의 고유값들의 합을 최소화하는 것이며[10], 위 식을 풀기 위해 각 k 번째 Xk에 대해 식 (11)과 같이 나타낼 수 있다.
여기서 δ는 정규화 상수, I는 단위행렬이며, 랭크가 1 보다 큰 경우에 한 해, 최적해는 고유값 분해를 통해 X=σuuT를 획득할 수 있다[11]. 여기서 σ는 고유값이며, u는 고유값에 해당되는 고유행렬이다. 즉, 이를 통해 구하고자하는 소자별 크기/위상 벡터 신호는 로 구할 수 있다.
설계하고자 하는 주엽이 넓은 광역빔을 최적화 설계하기 위해서는 식(12)와 같은 제한조건이 있다.
주엽레벨은 하한 l(θ)과 상한 u(θ) 내에 존재해야 하며, 부엽레벨은 어떤 ρ(θ)값 이하여야 한다는 조건이다. 식 (12)에 식 (8) 및 SDR을 적용하면 식 (13)과 같이 표현할 수 있다.
소자의 크기는 고정시키고 위상만은 이용하여 최적화를 수행해야 하기 때문에 식 (6)과 식 (8)로부터 소자 N개의 크기값은 식 (14)와 같이 설정된다.
식 (14)를 제한조건으로 바로 사용하기에는 어려움이 있다. 왜냐하면 소자크기 고정 제한조건을 만족시키기 위한 해는 비교적 쉽게 구할 수 없기 때문이다. 따라서 본 논문에서는 배열소자의 크기를 소수점 셋째자리까지 같도록 αn과 βn을 두어 제한조건을 설정하였고, 이로써 최적해를 쉽게 획득함을 확인하였다. 식 (13)과 식 (14)의 범위를 설정하여, 배열소자의 위상값을 구하기 위한 최종적인 convex 최적화 식은 식 (15)와 같다.
Ⅳ. 최적화 알고리즘 적용 및 분석
본 절에서는 제안된 위상조정 convex 최적화 알고리즘을 검증하기 위해 목적 광역빔을 설정하고 최적화를 수행한다. 제안 최적화 알고리즘의 성능을 검증하기 위해 휴리스틱한 방법인 유전알고리즘으로 설계된 패턴[12]과 비교하였다. 표 1에는 목적 광역빔 및 안테나 변수를 정리하였다. 최적화 시뮬레이션은 편의성을 위해 1D 배열을 고려하여 수행하였다.
| Wide beam beam width | 9° |
| Side lobe level of wide beam | ≤−10 dBc |
| Array number | 56 |
안테나 개구면의 배열 크기를 고려하여, 배열소자의 크기와 위상을 조정하지 않았을 때, 실제 빔폭은 2~3도이다. 한정된 시간에 효과적인 탐색을 위해 송신빔에 적 용되는 광역빔은 9도로 설정하였고, 부엽레벨은 수신빔의 부엽레벨(약 −40 dBc)를 고려하여 −10 dBc로 설정하였다. 광역빔의 빔폭이 넒어질수록 부엽레벨은 높아지는 경향을 가지기 때문에 −10 dBc로 설정한 것은 적절한 것으로 보인다. 우선 유전알고리즘[11]으로 적용한 최적화 결과 패턴은 그림 2와 같다.
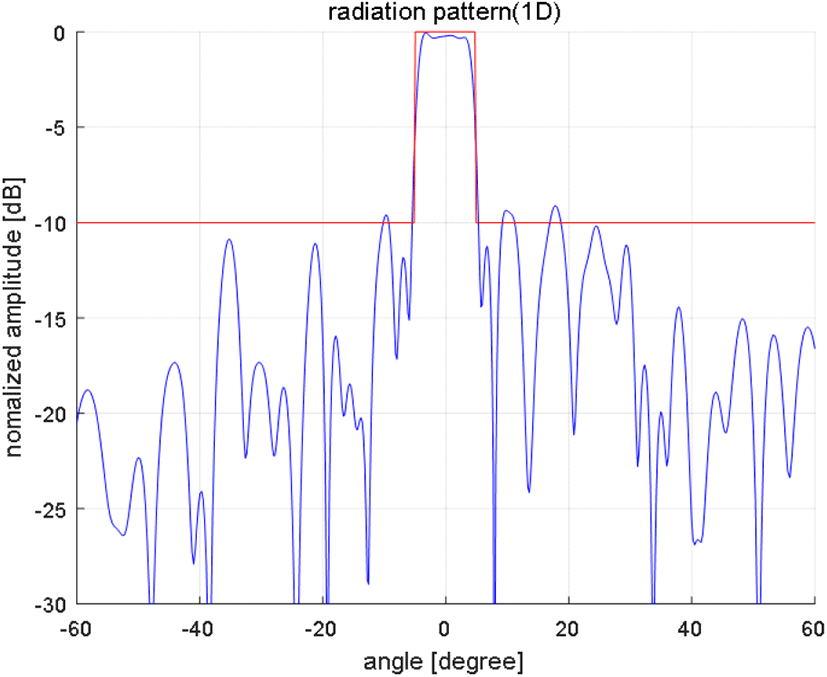
패턴 결과를 보면 최적해를 찾아가려고 하지만, 주엽레벨에서의 리플 및 부엽레벨 결과, 최적의 광역빔을 설계하지 못한다. 일반적으로 광역빔보다 좀 적은 약 5도 정도의 빔폭을 갖는 빔은 유전알고리즘을 이용하여도 쉽게 설계가 가능하지만, 9~12도 정도의 빔은 주엽부분에서 리플이 많이 생기거나, 아니면 부엽레벨이 많이 올라오는 문제점이 생긴다.
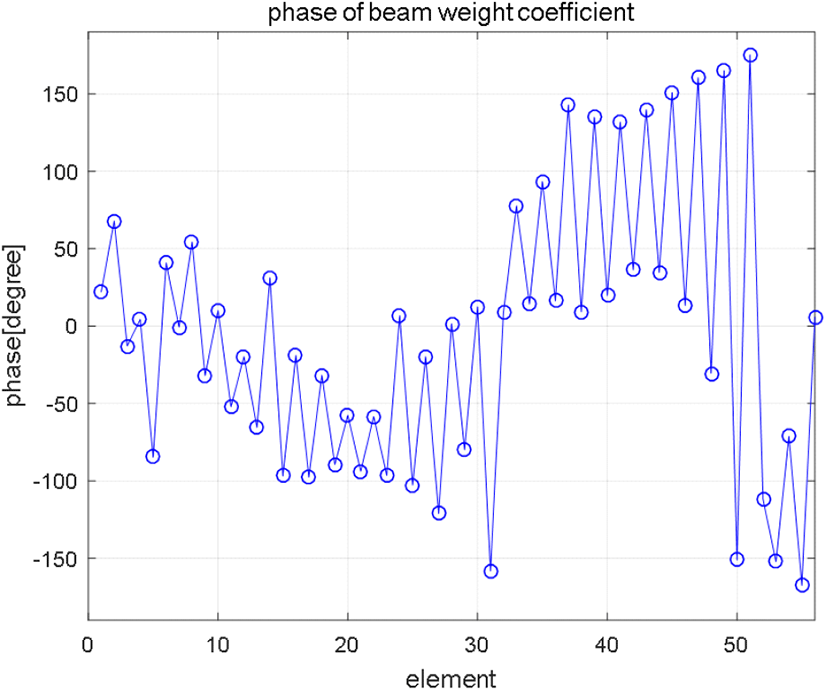
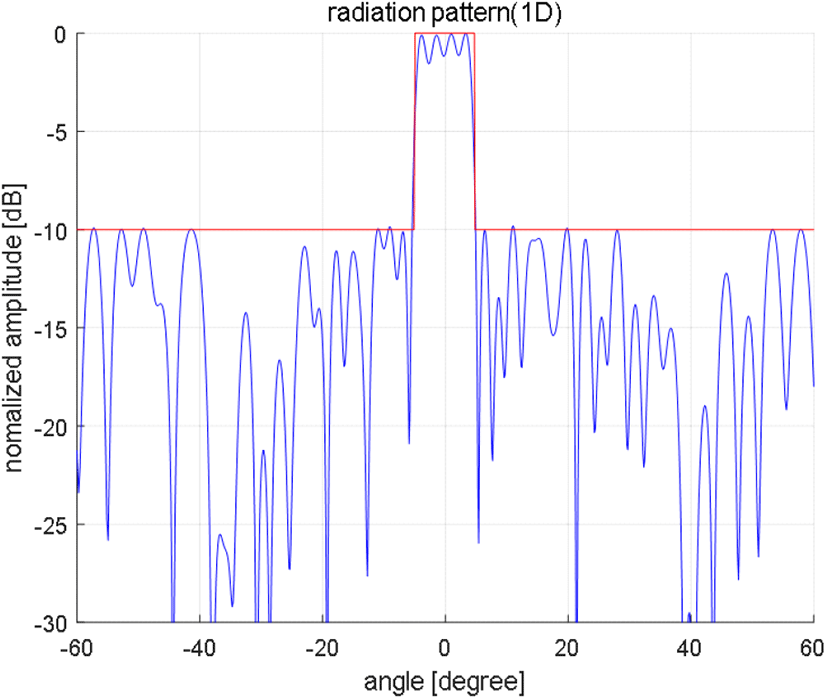
제안 알고리즘을 적용하여 획득한 56개 소자의 위상값은 그림 3과 같으며, 획득한 소자의 위상값을 이용한 빔패턴 결과는 그림 4와 같다. 식 (15)을 이용하여, 주엽레벨은 상한 0 dBc, 하한 −1.5 dBc를 만족하는 10도빔, 부엽레벨은 상한 −10 dBc로 설정하여 최적화를 수행하였다. 광역빔 패턴을 보아 알 수 있듯이 원하는 제한조건에 맞게 잘 설계된 것을 알 수 있다. 유전알고리즘 설계결과와 제안 알고리즘을 이용한 설계 결과와의 비교 결과는 표 2와 같다. 제안 알고리즘이 유전알고리즘보다 주엽하한 레벨이 조금 더 작지만, 빔폭 및 부엽레벨 면에서 우수하 며, 또한 알고리즘 별 수행 시간을 비교해 볼 때에도 훨씬 우수한 성능을 가진다. 그리고 유전알고리즘의 빔형태는 3 dB 빔폭을 기준으로 위로 올라갈수록 빔폭이 좁아지는 경향을 가지지만, 제안 알고리즘의 빔폭은 거의 일정한 것을 확인할 수 있다.
| Goal specification | Genetic algorithm[12] | Proposed algorithm | |
|---|---|---|---|
| Beam width | 9° | 9.16° | 9.08° |
| Lower level of main lobe | −1.5 dBc | −0.31 dBc | −1.43 dBc |
| Side lobe level | −10 dBc | −9.14 dBc | −9.8 dBc |
| Total time | - | 120 min | 32 min |
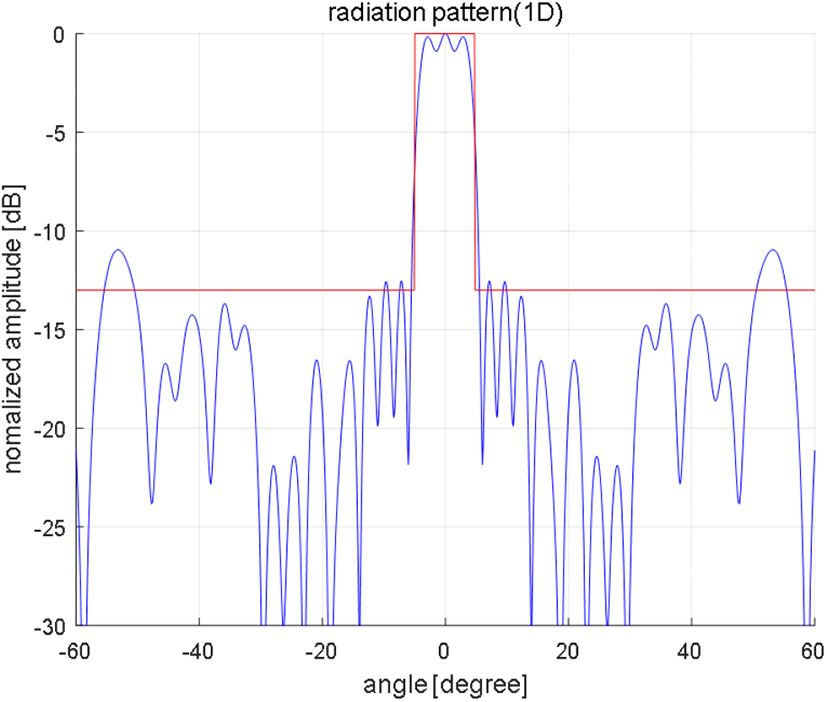
추가적인 비교 분석을 위해 부엽레벨의 상한 크기를 −13 dBc로 설정하여 최적화를 수행해보았다. 유전알고 표 2. 알고리즘 비교 분석 결과 리즘을 이용한 최적화 결과는 그림 5로 부엽레벨은 더 내려 가지만 그림 2보다 주엽레벨에서 더 큰 리플을 가지는 단점이 있다. 하지만 위상조정 convex 최적화 방법을 이용하면, 주엽레벨의 상하한 크기 및 부엽레벨을 만족하는 최적해가 존재하지 않아, 원하는 광역빔을 만들 수 없다. 즉, 위상조정 convex 최적화 방법의 단점은 제한조건을 만족하는 최적해가 존재하지 않을 경우, 원하는 해를 구할 수 없다는 것이다. 즉, 위상조정 convex 최적화 방법을 이용하여 광역빔 최적화를 수행할 때, 주엽의 빔폭, 부엽레벨의 크기를 적절히 trade off하는 과정이 필요하다.