Ⅰ. 서 론
압축센싱 기법은 전통적 표적 방위각 추정기법과는 별개로 신호의 희소성(sparsity)을 이용하여 표적 방위각을 추정하는 기법이다. 압축센싱 기법은 데이터 행렬 fitting 방식[1]~[3]과 공분산 행렬 fitting 방식으로 나눠진다[4],[5]. SpSF(Sparse Spectrum Fitting) 알고리즘[4]과 SPICE 알고리즘[5]은 대표적인 공분산 행렬 fitting 기반 도래각 추정 알고리즘이다[5]. SpSF 알고리즘은 sparse recovery를 구현하기 위하여 수치적 최적화를 수행해야 하므로 계산량이 많다. 반면 SPICE 알고리즘은 반복계산(iteration)을 통해 수식적인 최적화 과정 없이 표적 방위각 추정이 가능하므로 SpSF 알고리즘에 비하여 계산량이 적은 장점이 있다.
본 논문에서는 기존의 시간영역에서 다룬 SPICE 알고리즘을 주파수 영역으로 확장하기 위해서 주파수 영역에서 공분산 행렬을 유도했고, 이를 SPICE 알고리즘에 적용함으로써 주파수 영역에서도 해당 알고리즘을 구현할 수 있음을 보인다. 주파수 영역에서 SPICE 알고리즘의 표적 방위각 추정 성능을 알아보기 위해 전통적 표적 방위각 추정 알고리즘인 CBF(Conventional Beamforming), MVDR (Minimum Variance Distortionless Response) 알고리즘과 비교 분석한다[1]~[3],[6].
Ⅱ. 본 론
M개의 센서로 구성된 선형배열에서 수신한 데이터 y(t)는 다음과 같이 표현할 수 있다[6].
k는 탐색각도의 인덱스 값이고, M은 센서의 개수이며, 탐색각도 개수는 Nθ이다. sk(t)는 θk로 입사한 신호이고, ak는 센서 응답을 담고 있는 센서 어레이 벡터이다. n(t)는 평균이 0이고 분산은 σ2인 정규분포를 따르는 랜덤변수를 성분으로 갖는 랜덤벡터이다.
SPICE 알고리즘은 공분산 행렬에 sparse recovery 기법을 적용함으로써 표적 방위각을 추정하는 기법이다. 수신 데이터를 주파수 영역에서 SPICE 알고리즘에 적용하여 표적 방위각을 추정하려면 시간영역에서의 수신 데이터를 주파수 영역으로 변경한 후, 공분산 행렬을 구현해야 한다.
시간영역의 수신신호 행렬을 일정한 사이즈의 여러 block으로 나눈 후, 각 block 별로 FFT(Fast Fourier Transform)를 수행함으로써 주파수 영역으로 변환하고 센서별 입사 tone 신호가 있는 bin의 데이터를 이용하여 벡터를 생성한다.
주파수 영역의 수신 신호 행렬 중 b번째 block에 대한 수신 신호 행렬 은 다음과 같이 정의가 가능하다.
식 (5)에서 N은 FFT의 길이다. 주파수 영역에서 b번째 block의 수신 신호 벡터 Yb(fi)는 다음과 같이 나타낸다.
각 block에 대한 주파수 영역의 수신신호 벡터를 이용하여 주파수 영역의 수신신호 행렬을 구한다. 주파수 영역의 공분산 행렬은 다음과 같이 정의된다. B는 block 개수이다.
주파수 영역의 수신신호 행렬을 이용하여 앙상블 평균으로 구한 신호 공분산 행렬과 잡음 공분산 행렬은 다음과 같이 정의할 수 있다.
앙상블 평균으로 구한 공분산 행렬은 다음과 같이 표현 할 수 있다.
A와 P는 다음과 같이 정의할 수 있다.
P 행렬의 1번째 성분부터 Nθ번째 성분까지의 초기 추정 값은 빔형성을 이용하여 추정한 스펙트럼 결과 값으로 설정하고, 잡음 행렬 P의 Nθ+1번째 성분부터 Nθ+M번째 성분의 초기값은 σ값으로 설정한다.
SPICE 알고리즘은 다음 과정을 통해 가장 sparse한 대각성분 p값들을 갖는 P행렬을 찾음으로써 표적 방위각과 전력을 추정할 수 있다[3]~[5].
Ⅲ. Simulation Results
본 논문에서 제안한 방법을 수동소나로부터 수신한 데이터에 적용함으로써 주파수 영역의 공분산 행렬을 구한 후, 이를 이용하여 CBF, MVDR 그리고 SPICE 알고리즘을 구현한다. 해당 알고리즘들을 이용하여 표적 방위각을 추정하고, SPICE 알고리즘의 추정성능을 CBF, MVDR 알고리즘의 추정 성능과 비교함으로써 SPICE 알고리즘의 추정 성능을 분석한다.
| Design frequency [Hz] | 800 |
| # of snapshot in time domain | 2,048 |
| Length of FFT | 2,048 |
| Velocity of sound wave [m/s] | 1,500 |
| Interelement space d | λ/2 |
| Search range [deg.] | 0°~180° |
시뮬레이션은 표 2와 같이 세 가지 경우에서 수행했다.
| Freq. [Hz] | Angle [Deg.] | SNR [dB] | Sensor | Block | |
|---|---|---|---|---|---|
| Case 1 | 790 | [30°, 75°] | 0 | 15 | 15 |
| 800 | |||||
| Case 2 | 799.9 | [30°, 75°] | 2 | 15 | 15 |
| 800 | |||||
| Case 3 | 800 | [30°, 75°] | −5 | 15 | 15 |
| 800 |
Case 1과 2인 경우, 다수 개의 uncorrelated 신호가 입사할 때 수신 데이터 FFT하여 다수개의 신호 에너지가 같은 bin에서 발생할 수 있도록 하기 위해 임의로 설정했다.
Case 1인 경우는 두 신호가 서로 다른 주파수를 가지므로 주파수 영역으로 구현된 세 가지 알고리즘들이 신호 에너지가 존재하는 bin 위치에 따라서 개별적으로 표적 방위각을 추정한다. SNR이 0 dB이며, 모의 신호의 전력 값은 2 dB이고, 해당 시뮬레이션의 결과 스펙트럼은 그림 2와 같이 나타난다.
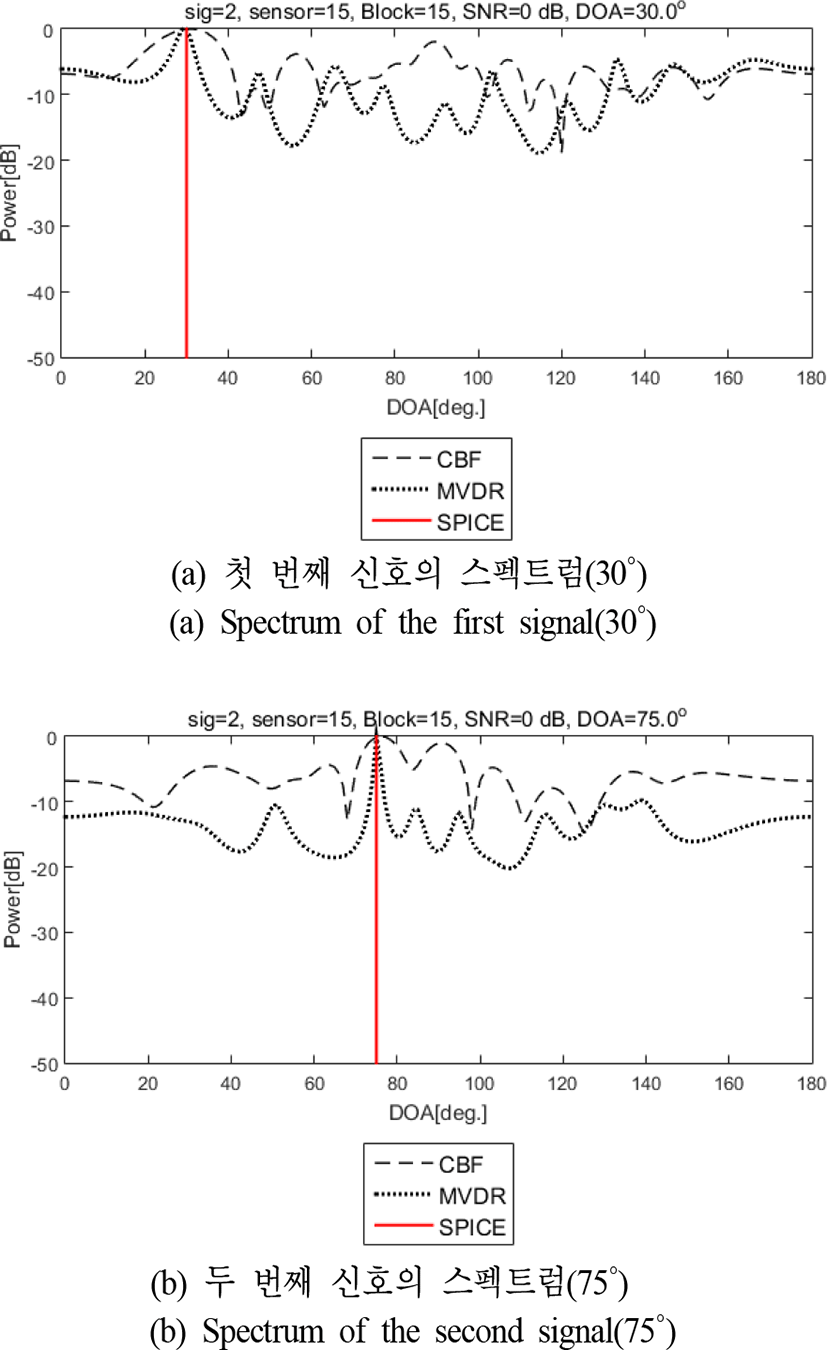
그림 2에서 SPICE 알고리즘이 제대로 표적 방위각을 추정하고, 다른 알고리즘은 추정 오차가 발생함을 알 수 있다. 또한, SPICE 알고리즘의 스펙트럼이 peak 주변에서 가장 뾰족하므로 SPICE 알고리즘의 성능이 가장 우수함을 알 수 있다.
Case 2인 경우에는 입사한 두 신호가 서로 다른 주파수를 가지고 있지만, 주파수 영역으로 변경 시 FFT 길이는 시간영역의 샘플 수와 같으므로 신호 에너지가 같은 bin 위치에 존재한다. SNR이 2 dB이며 모의 신호의 전력 값은 3.1698 dB이고, 세 알고리즘을 이용하여 표적 방위각 추정을 수행하였고, 해당 결과 스펙트럼은 그림 3과 같다.
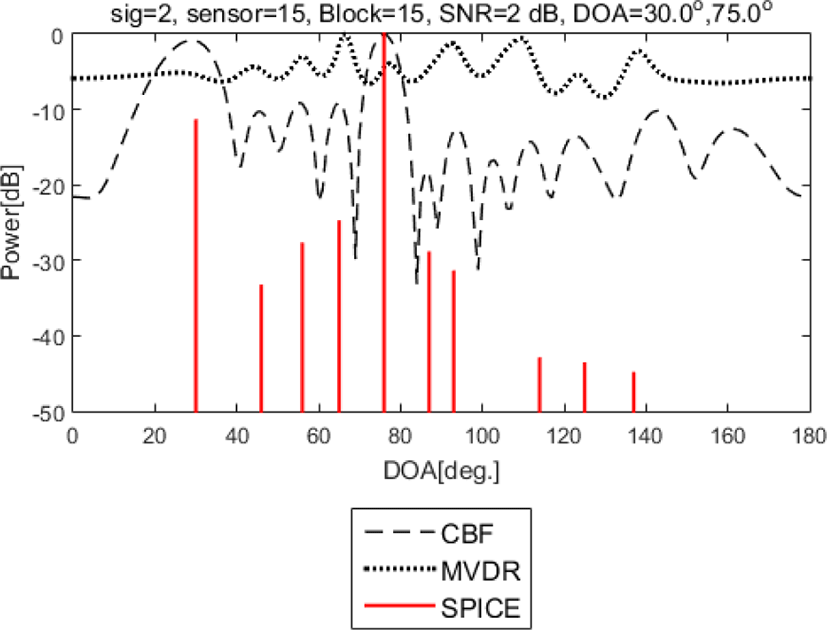
그림 3에서 CBF인 경우는 75° 입사 신호만 추정되고, MVDR인 경우는 30° 입사 신호만 추정되며, 나머지 각도 입사 신호는 추정되지 않음을 알 수 있다. SPICE인 경우는 신호가 입사한 위치에서 가장 큰 스펙트럼을 가지므로 방위각 추정이 가능함을 알 수 있다.
Case 3인 경우에 SNR이 −5 dB이며, 모의 신호의 전력 값은 0.6325이다. 그림 4는 같은 주파수를 가진 다수의 신호가 입사한 경우의 각 알고리즘의 추정 결과 스펙트럼이다.
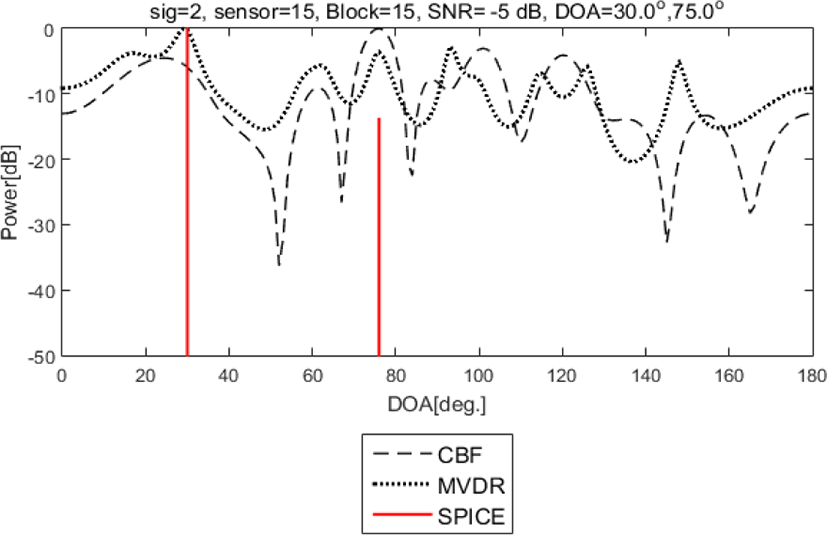
Correlated 신호가 센서 배열에 입사할 때, 신호 서로 간의 간섭 때문에 알고리즘의 방위각 추정 성능이 저하된다. 그림 4를 보면 SPICE 알고리즘을 이용할 때만 정확한 방위각 추정을 하고, 나머지 알고리즘을 이용 시 정확한 방위각 추정이 불가능함을 확인할 수 있다.
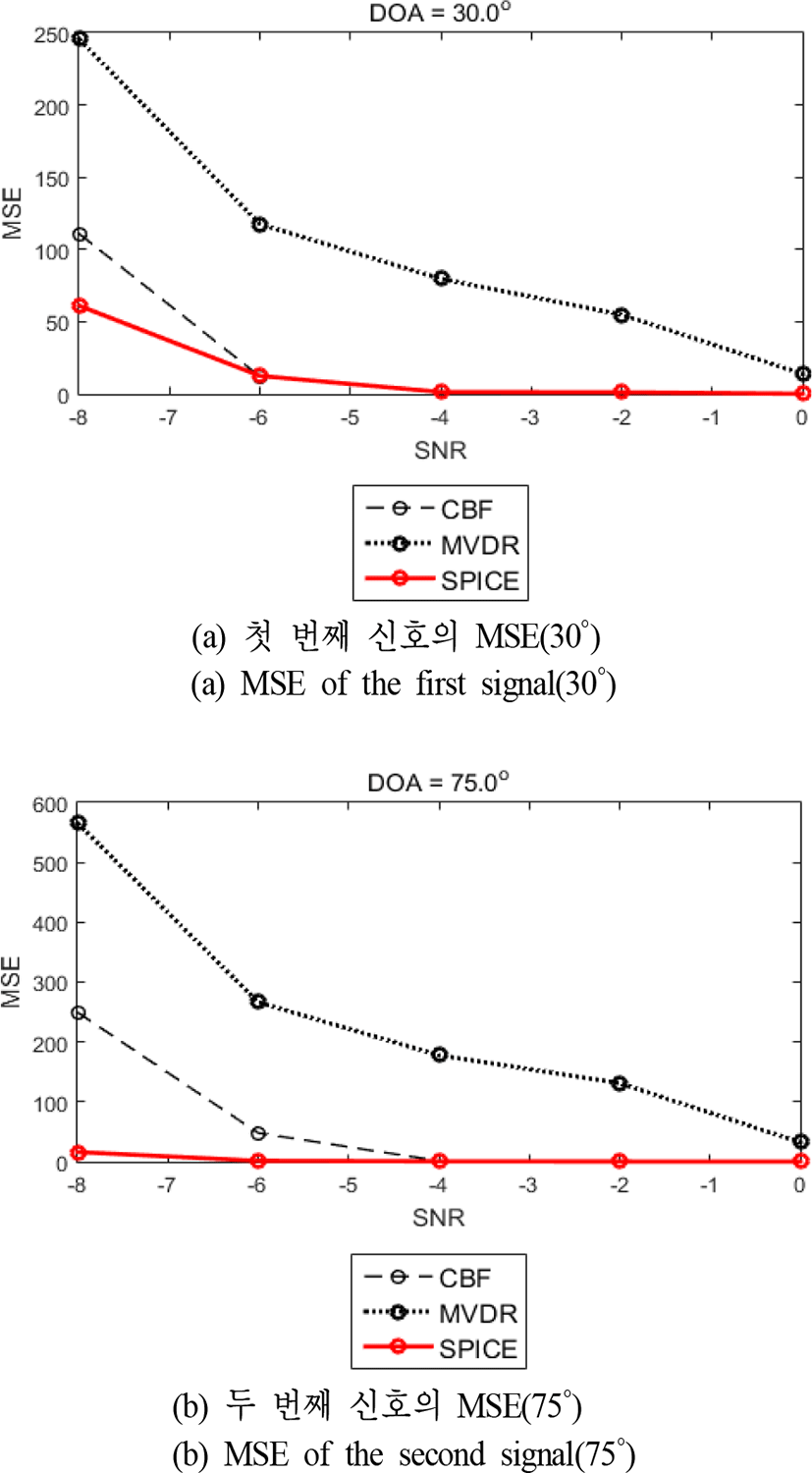
세 가지 알고리즘의 표적 방위각 추정 성능을 분석하기 위해 case 2인 시뮬레이션 환경에서 SNR이 −8 dB와 0 dB 구간에서 2 dB 간격으로 변화하고, 1,000번 반복하여 구한 MSE(Mean Square Error) 를 그림 5와 같이 나타내었다.
그림 5를 통해 SPICE 알고리즘의 MSE 값이 전 SNR 구간에서 가장 작게 나오는 것을 확인할 수 있고, 이를 통해 SPICE 알고리즘의 추정성능이 다른 표적 방위각 추정 알고리즘보다 더 우수함을 알 수 있다.
SPICE 알고리즘은 볼록 최적화를 하지 않아 기존의 공분산 fitting 기반 알고리즘인 SpSF보다 계산량이 적다는 장점을 갖고 있다. 두 알고리즘의 계산량 비교를 위해 다음의 시뮬레이션을 수행했다. Case 2의 실험 조건 하에서 SPICE 알고리즘과 SpSF 알고리즘의 수행시간을 구했으며 MATLAB 함수를 이용하여 시간 측정을 진행했다. 다음 표 3은 해당 환경에서의 SPICE 알고리즘과 SpSF 알고리즘 의 수행시간을 보인다.
| Algorithms | Operation time (sec) |
|---|---|
| SPICE | 0.5528 |
| SpSF | 96.6935 |
SpSF인 경우, 볼록 최적화를 통해 최적의 희소 신호공분산행렬을 구하고, 이를 통해 도래각 추정을 수행한다. 볼록 최적화는 계산량이 많아 최적화 과정을 진행하는데 많은 수행시간을 요구하게 된다. 이에 반하여 SPICE는 볼록 최적화를 이용하지 않기에 SpSF 알고리즘에 비해 적은 계산량이 요구된다.
Ⅳ. Conclusion
본 논문은 기존의 시간영역에서 다룬 SPICE 알고리즘을 주파수 영역으로 확장하였다. 주파수 영역으로 확장하기 위해 주파수 영역에서 공분산 행렬을 구현했고, 이를 SPICE 알고리즘에 적용해서 시뮬레이션을 통해 주파수 영역으로 확장 가능함을 보여 주었다. 주파수 영역에서 표적 방위각 추정 성능을 분석하기 위해 여러 시뮬레이션 조건에서 CBF, MVDR 그리고 SPICE 알고리즘을 수행했고, 이를 통해 SNR이 낮은 경우나 correlated 신호가 입사한 경우에서는 전통적인 표적 방위각 추정 알고리즘에 비해 SPICE 알고리즘의 표적 방위각 추정 성능이 더욱 우수함을 보여 주었다.