Ⅰ. 서 론
단일 또는 주기구조로 구성된 소형 개구에서 전자파 투과 특성에 대한 연구는 꾸준히 진행되고 있다[1]. 기존 소형 개구의 전자파 투과 특성을 관찰하기 위해서 일반적으로 개구가 완전도체로 이루어져 있을 때를 가정하고 전자파 특성을 계산하였다. 하지만 테라헤르츠 주파수에서는 마이크로파 영역에서와 같이 완전 도체의 물질 특성을 그대로 적용할 수 없기 때문에 기존의 해석 방법을 활용하여 전자파 특성을 계산하기에 어려움이 따른다. 따라서 테라헤르츠 주파수 대역에서 실제 금속의 물질 특성을 고려하여 소형 개구의 전자파 특성을 계산하는 방법이 소개되었다[2],[3]. 개구 투과 현상을 해석하기 위한 수치해석 방법은 비교적 다양하지만[4],[5], 모드정합법[2],[3]을 사용하면 모드별 필드 관찰을 통해 전자파의 전송 원리를 이해하기가 용이하다.
이와 같은 장점을 바탕으로 모드정합법을 적용하여 금속과 절연체로 이루어진 소형 개구가 주기적으로 구성되어 있을 때 전자파 특성을 계산하였으나, 다양한 주파수에 의한 금속의 물질 특성이 반영되지 않고 특정 주파수에서 투과 특성만 관찰하였다[2]. 또한 폭넓은 테라헤르츠 주파수 영역에서 실제 금속 물질 특성을 반영하여 투과 특성을 도출한 연구가 수행되었으나, 주기구조가 아닌 단일 개구에 의한 투과 특성만을 고려하였다[6].
본 논문에서는 완전 도체 혹은 테라헤르츠 영역에서 유전 특성을 고려한 금의 주기구조로 구성된 소형 개구에서 투과 특성을 고찰하였다. 이를 위해 테라헤르츠 주파수에 따른 금의 물질특성을 반영하는 것뿐만 아니라, 소형 개구 사이의 거리, 금속의 두께 등을 변화시키며 투과 특성의 변화를 확인하였다. 도출된 개구특성은 광학 영역에서 분배기, 스플리터, 스위치, 모드 변환기 등의 금속 도파관 특성 분석에 적용이 가능할 것으로 사료된다[7].
Ⅱ. MIM 도파관의 구조 및 투과 전력
그림 1은 자유공간, MIM(Metal-Insulator-Metal) 도파관, 자유공간의 3 영역으로 구성된 해석 구조를 나타낸다. 이 때 주기구조의 MIM 도파관은 금속과 절연체가 반복되는 형상의 주기적 개구를 가진다. 2차원 소형 개구는 주기 p를 갖고, y-축 방향으로 무한하게 존재하며, 소형 개구의 너비는 2g, 금속의 너비는 2d, 진행 방향으로 두께는 t이다. 왼쪽 자유 공간으로부터 소형 개구에 입사하는 입사파는 수평 편파 모드로 수직으로 입사하는 경우만 가정하였으며, 오른쪽 자유 공간으로 소형 개구를 통과하는 투과파를 입사파 전력밀도로 나누어 투과율을 계산한다.
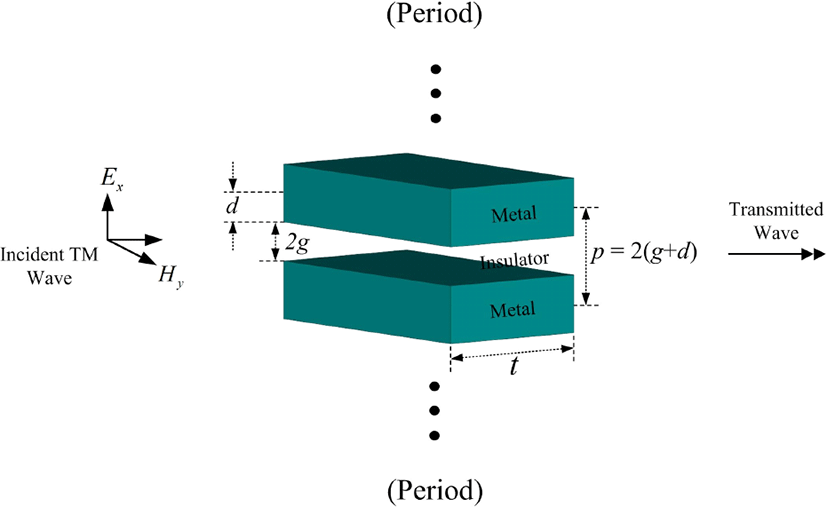
식 (1)은 그림 1의 MIM 도파관에서 분산방정식을 나타낸 것이며, 식 (2)는 횡방향 전파상수 사이의 관계를 나타낸 것이다[2],[6]. 이때 식 (1), (2)에는 ejωt의 위상 항이 적용되었다.
εm와 εi는 각각 금속과 절연체의 비유전율 값을 나타내며, kz,n은 z축을 따라 진행하는 n번째 전파상수를 의미한다. κm,n과 κi,n은 금속과 절연체의 n번째 횡방향 전파상수를 의미한다. 이때 적용하는 금의 유전율[8]εm은 50 THz에서 −1383.2-j367.24, 200 THz에서 −94.108-j7.567이며, 절연체는 진공으로 가정하므로 εi를 1로 고정한다.
그림 2는 MIM 도파관의 주기 p가 0.5λ0, 간격 2g이 0.05λ0이며, 금속 금(Au)의 주파수가 50 THz일 때 정규화된 횡방향 전파상수 κm/k0의 포인트 스펙트럼과 이산화된 연속 스펙트럼(Discretized Continuous Spectrum: DCS)을 나타낸 것이다[2],[6],[9]. 포인트 스펙트럼에서 고유치(✴)는 절연체에서 사인파의 고조파를 표현하며, 유전체 도파관에서 도파 모드(guided mode)와 기능이 유사하다. 실수부가 가장 큰 값을 가질 때, 첫 번째 TM 모드인 TM0 모드의 고유치가 되며, 모드정합법으로 계산하여 투과 계수를 구할 경우 투과에 가장 크게 영향을 미치는 부분이 된다. 이어지는 포인트 스펙트럼의 해들은 다음 TM 모드의 고유치들을 나타낸 것이며, 허수값은 점차 증가하고 실수값은 감소하는 형태로 나타나지만, 투과 특성에는 큰 영향을 미치지 않는다. 다음으로 DCS의 고유치(O)는 절연체 영역이 아닌 금속 영역에서 사인파의 고조파를 나타내며, 유전체 도파관(dielectric slab waveguide) 구조에서 일반적으로 관찰되는 방사 모드(radiation mode)의 필드 형상과 유사하다. 포인트 스펙트럼과 유사하게 실수부가 0에 가까운 고유치일수록 낮은 고조파를, 멀어지는 고유치일수록 높은 고조파를 표현한다. 하지만, DCS는 식 (2)에 대입하여 kz,n의 값을 통해 확인할 수 있듯이 전자파의 전파에는 크게 영향을 미치지 못하여 경계 조건을 만족시킬 뿐이다. 포인트 스펙트럼은 사인파의 형태가 절연체 영역에 집중되어 있어서 절연체 영역에서 다양한 필드 형태를 퓨리에 시리즈의 조합으로 설명할 수 있으며, DCS는 사인파의 형태가 금속 영역에 집중되어 있어서 금속 영역에서 다양한 필드의 형태를 퓨리에 시리즈의 조합으로 나타낼 수 있다. 이 두 가지 스펙트럼의 조합을 통해 모드의 완성도(completeness)를 형성한다. 그림 2의 전체 해의 결과는 κm의 허수부가 양수인 경우만 나타내었지만 반대로 음수인 경우에도 나타낼 수 있으며, 각각의 해는 원점을 중심으로 일대일 대응하며, 식 (1), (2)에도 동일하게 만족된다.
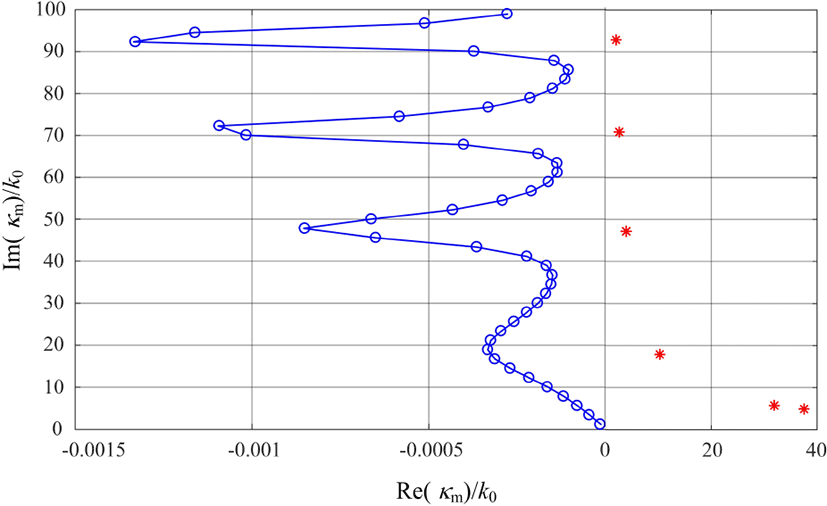
그림 2로부터 구한 고유치와 모드정합법[6]을 통해 전자파의 투과율 τ를 식 (3)과 같이 표현할 수 있다.
Wi는 입사파 전력밀도를, Pt는 투과 전력을 의미하며, 투과 전력은 그림 2에서 MIM 도파관과 오른쪽 자유공간의 경계면에서 Et와 Ht의 값을 통해 적분한 후 실수 값을 취하여 구할 수 있다. 이 때, Et와 Ht는 MIM 도파관과 자유공간의 경계면에서 접선 성분의 투과 전기장 및 자기장을 의미하며, 위첨자 *는 켤레 복소수를 나타낸다.
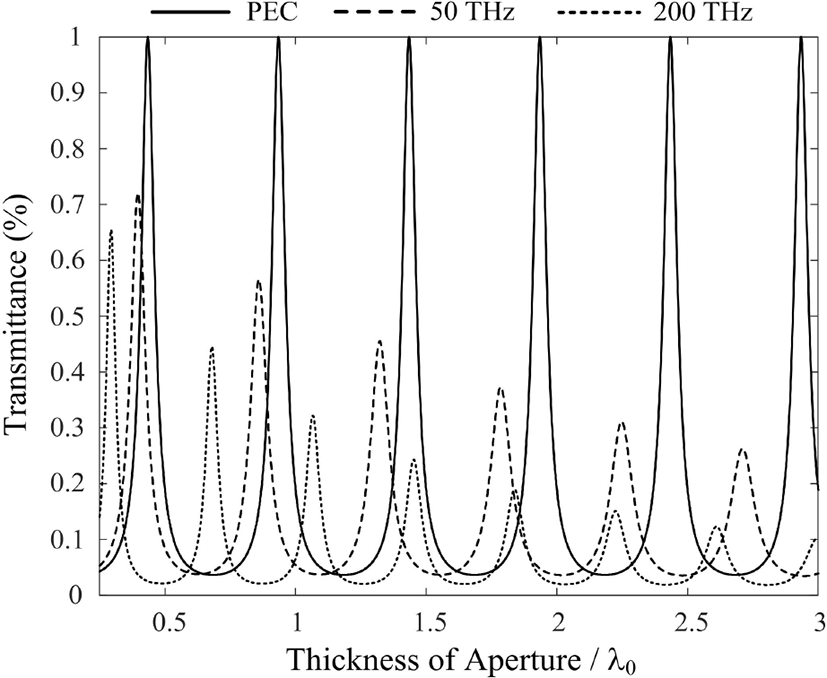
그림 3은 MIM 도파관에서 주기 p가 0.5λ0, 개구의 간격 2g가 0.05λ0일 때 금속의 두께에 따른 투과율을 식 (3)을 활용하여 나타낸 것이다. 완전도체, 50 THz, 그리고 200 THz의 금의 경우 각각의 투과 특성을 나타낸 것이며, 완전도체의 경우 도체에 의한 손실이 없기 때문에 최대 투과율 1이 t가 (0.435 + 0.5n)λ0 (n=0, 1, 2, ⋯)일 때, 주기적으로 나타난다. 반면에 실제 금속인 금의 경우, 유한한 유전율의 값에 의해 손실이 반영되므로 금속의 두께가 증가함에 따라 투과율의 감쇠를 확인할 수 있으며, 주파수가 높을수록 감쇠가 심해지는 경향을 보인다. 즉, 50 THz의 경우 금속의 두께가 0.397λ0일 때 최대 투과율 값이 0.72이며, 200 THz의 경우 금속의 두께가 0.294λ0일 때 최대 투과율의 값이 0.654이다. 이와 같은 차이는 표 1에서 정규화된 전파 상수 kz,0/k0의 허수값을 통해 확인할 수 있다. 또한 kz,0/k0의 실수값의 비교를 통해 200 THz의 경우 투과전력 첨둣값의 간격이 50 THz의 경우에 비해 좁아짐을 확인할 수 있다[6].
| Fig. 3 | kz,n/k0 (n = 0) | Fig. 4 | kz,n/k0 (n = 0) |
|---|---|---|---|
| PEC | 1 | PEC | 1 |
| Au @ 50 THz | 1.0804 − j 0.0101 | Au @ 50 THz | 1.0410 − j 0.0053 |
| Au @ 200 THz | 1.2944 − j 0.0156 | Au @ 200 THz | 1.1572 − j 0.0088 |
그림 4는 MIM 도파관에서 주기 p가 0.5λ0, 개구의 간격 2g가 0.1λ0일 때 금속의 두께에 따른 투과율을 식 (3)을 활용하여 나타낸 것이다. 그림 3에서와 같이 완전도체, 50 THz, 그리고 200 THz의 금의 경우 각각의 투과 특성을 나타낸 것이며, 완전 도체의 경우 최대 투과율 1이 t가 (0.412 + 0.5n)λ0 (n = 0, 1, 2, ⋯)일 때, 주기적으로 나타난다. 그림 3에 비해 개구의 폭이 더 넓기 때문에 투과율의 값이 전체적으로 큼을 확인할 수 있으며, 그림 3과 마찬가지로 표 1을 통해 투과 현상을 이해할 수 있다.
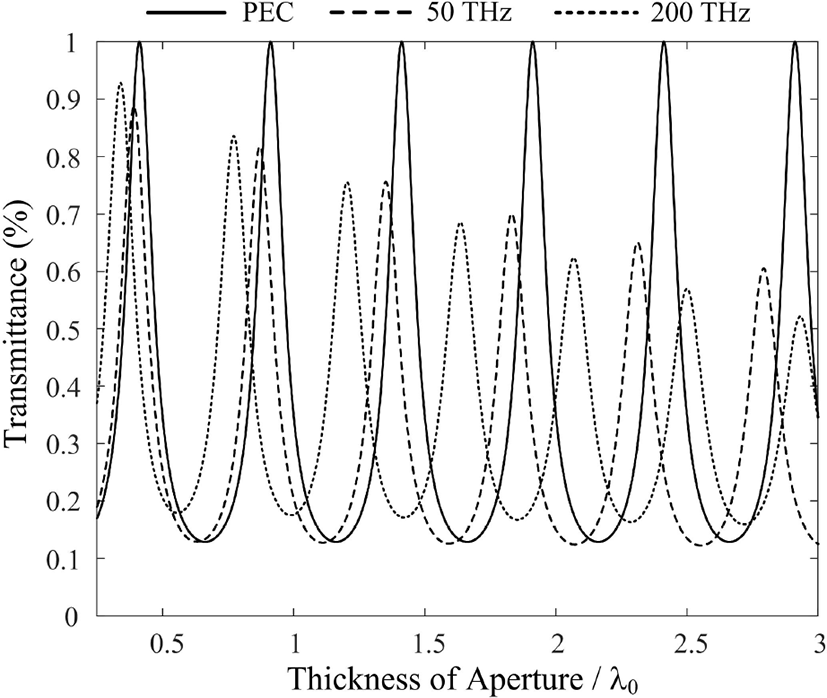
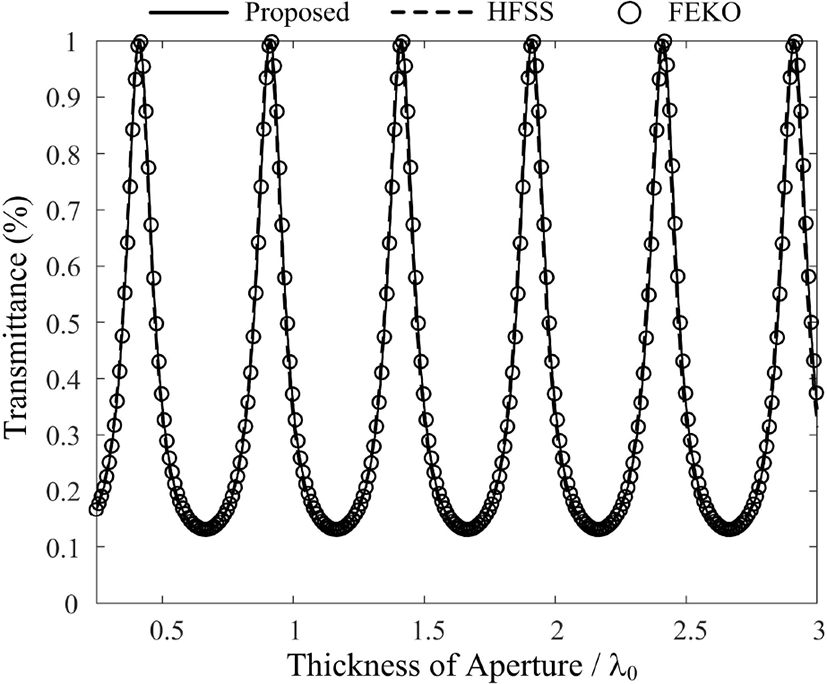
그림 5는 모드 정합법을 이용하여 도출된 투과특성에 대한 정확도를 검증하기 위해 상용 소프트웨어인 ANSYS사의 HFSS와 Altair사의 FEKO 시뮬레이션을 이용하여 비교한 결과를 보여준다. MIM 도파관의 주기 p가 0.5λ0, 개구의 간격 2g가 0.1λ0일 때 금속의 두께에 따른 투과율을 계산하였으며, 도출된 3개의 결과가 매우 유사함을 확인하였다.
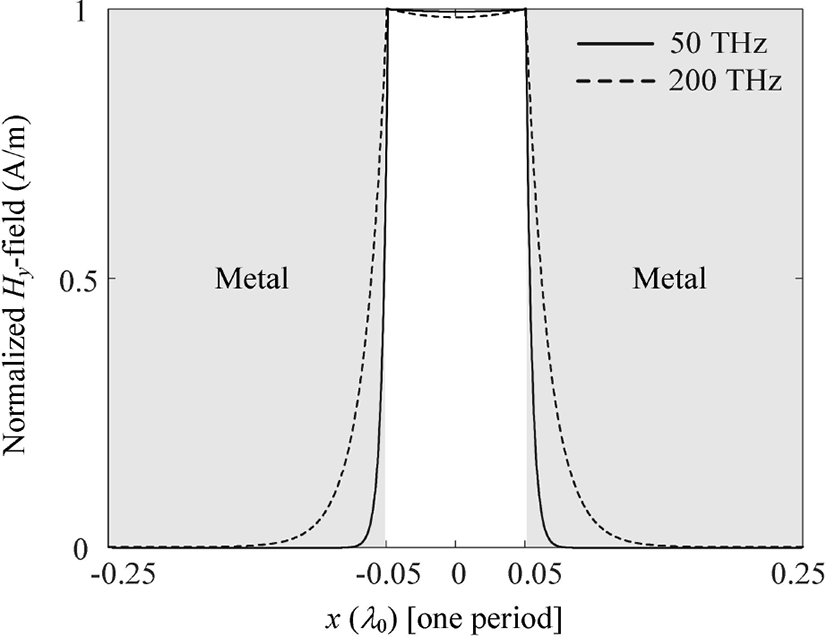
마지막으로 그림 3의 경우 200 THz에서 전체적인 투과율의 특성이 50 THz에 비해 낮은 값으로 나타나지만, 그림 4의 경우에는 MIM 도파관의 두께가 얇은 경우 (t < 1λ0)에도 200 THz의 투과율 첨둣값이 50 THz에 비해 높게 나오기도 한다. 이와 같은 사실은 전자파의 투과 특성에 가장 큰 영향을 미치는 TM0 모드의 필드 패턴을 통해서 이해할 수 있다. 그림 6은 기본 모드인 TM0 모드에 대한 Hy 필드의 패턴을 각 주파수별로 나타낸 것이다. 점선에서와 같이 200 THz에서 필드 패턴은 금속 영역으로 많이 흡수되지만, 50 THz의 실선은 금속 영역으로 필드의 영향이 작음을 확인할 수 있다. 이로부터 200 THz에서 MIM 도파관의 두께 t가 얇은 경우에 투과 영역으로 전자파가 많이 투과되는 것을 이해할 수 있으며, 그림 4에서도 확인할 수 있다.
Ⅲ. 결 론
본 논문에서는 테라헤르츠 주파수가 변함에 따른 금의 주기적인 소형 개구에 대한 투과 특성을 MIM 도파관의 두께가 변함에 따라 살펴보았으며, 그 결과를 완전도체의 경우와 비교해 분석해 보았다. 완전 도체의 경우는 투과율의 첨둣값이 0.5λ0의 주기로 일정하게 손실 없이 나타남을 확인할 수 있었지만, 테라헤르츠에서 실제 금속의 경우는 0.5λ0보다 작은 간격으로 투과량의 첨둣값이 나타났으며, MIM 도파관의 두께가 두꺼워짐에 따라 전체적인 투과량의 크기가 줄어듦을 확인할 수 있었다. 이와 같은 분석은 각 주파수 및 구조에서 첫 번째 모드의 정규화된 전파 상수와 자기장의 필드 패턴을 비교해 봄으로써 확인이 가능하다.




