논문/REGULAR PAPERS
UCA MIMO 전송 시 준직교적 빔 쌍을 활용한 합 전송률 향상 방안
양지영1, 김희원1, 성원진1,*
Sum-Rate Improvement Method Using Quasi-Orthogonal Beam Pairs for UCA MIMO Transmission
Jiyeong Yang1, Huiwon Kim1, Wonjin Sung1,*
1Department of Electronic Engineering, Sogang University
© Copyright 2019 The Korean Institute of Electromagnetic Engineering and Science. This is an Open-Access article distributed under the terms of the
Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits
unrestricted non-commercial use, distribution, and reproduction in any
medium, provided the original work is properly cited.
Received: Dec 04, 2017; Revised: Dec 29, 2017; Accepted: Jan 08, 2018
Published Online: Jan 31, 2018
요약
5G 이동통신시스템에서 요구되는 높은 주파수 효율을 달성하기 위해서는 대규모 다중 입출력 송수신(Massive Multiple-Input Multiple-Output: Massive MIMO) 기술의 활용이 필수적이며, 원소 수의 증가에 따라 다양한 형태의 어레이 형상이 사용될 수 있다. 본 논문에서는 균일 원형 어레이(Uniform Circular Array: UCA)를 사용하는 다중 사용자 MIMO 전송 시 활용 가능한 빔 형성 알고리듬을 제시하며, 빔 간 상관도를 활용하여 준 직교적인 빔 인덱스 쌍을 바탕으로 사용자간 간섭을 최소화하여 얻어지는 성능 이득을 평가한다.
Abstract
Massive multiple-input multiple-output (MIMO) transmission is an essential technique for achieving the high bandwidth efficiency required in 5G mobile communication systems. Various forms of arrays can be used as the number of antenna elements increases for massive MIMO transmission. In this letter, we propose a beamforming algorithm applicable to multiuser MIMO transmission using uniform circular arrays . By employing quasi-orthogonal beam pairs obtained from the inter-beam correlation information, we minimize inter-user interference and evaluate the resulting performance gain.
Keywords: Massive MIMO; UCA; Codebook; Orthogonality; Beamforming
Ⅰ. 서 론
대규모 다중 입출력 송수신(massive Multiple-Input Multiple-Output: massive MIMO) 전송 방식은 전송 속도 증가와 주파수 효율 향상을 위한 주요 기술로 활발히 연구되고 있다[1]. 다수의 송신 안테나를 이용하여 정확한 빔포밍 수행을 통해 신호의 멀티플렉싱, 다이버시티 이득을 증가시킬 수 있으며, 이를 위해 변형된 형태의 안테나 어레이를 활용하는 방안도 논의되었다[2]. 균일 원형 배열 (Uniform Circular Array: UCA) 안테나 구조를 위한 빔 형성 방식으로는 균일 선형 배열(Uniform Linear Array: ULA)을 위한 코드북을 변형시킨 방안들이 존재하며[3],[4], LoS 채널에 특화된 서브 어레이의 활용도 연구되었다[5]. 그러나UCA를 활용하는 다중 사용자 다중 랭크 전송을 위한 빔 형성 방안은 추가적인 연구가 필요한 상황이다.
본 논문에서는, 고정된 위치에 있는 다수의 사용자에게 동시 전송을 수행하는 점대다점(point-to-multipoint: P2MP) 환경에서 효율적인 빔 형성 방안을 제시한다. 형성한 빔 간 상관도 특성 분석을 통해 준직교적인 빔 쌍 규칙을 제안하고, 이를 통한 전송률 이득을 평가한다. 이후 내용으로는 Ⅱ장에서 시스템 모델, Ⅲ장에서는 균일 원형 배열을 위한 코드벡터를 설명하고, Ⅳ장에서 점대다점 빔형성 방식을 제안한다. Ⅴ장에서는 성능평가 결과를 제시하고, Ⅵ장에서 결론을 맺는다. AT는 행렬 A의 전치 행렬을 의미하며, AH는 행렬 A의 Hermitian을 의미한다.
Ⅱ. 시스템 모델
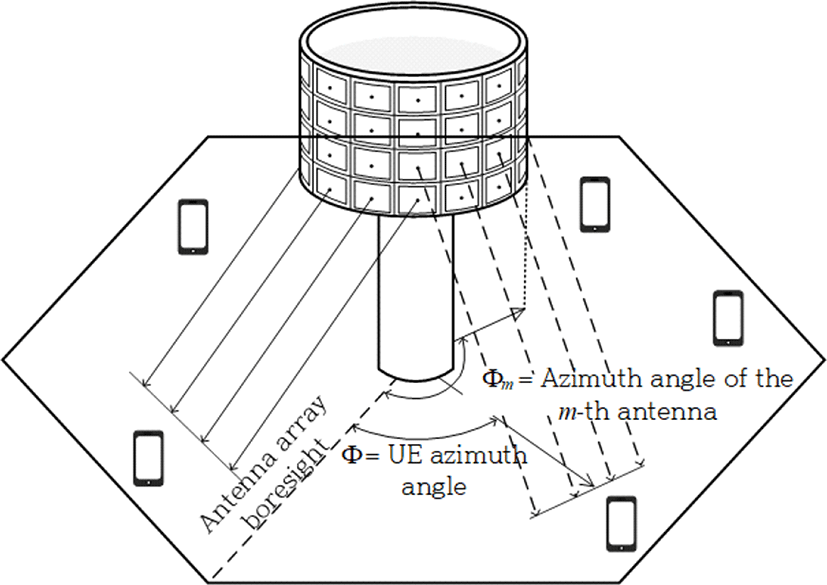
반지름이 R인 원 위에 동일한 간격으로 M개의 안테나원소를 배치하는 구조인 균일 원형 배열의 경우, 원소 간 거리는 d=2R sin(π/M)으로 결정된다. 이와 같은 어레이로부터 단일 안테나를 갖는 K 명의 다중 사용자에 전송 시 수신 신호는 으로 표시될 수 있다. 이때 는 M×K 크기의 채널 행렬로써 hk = [h1h2 ⋯ hM]은 k번째 사용자의 채널 벡터이다. W = [w1w2 ⋯ wK]는 K×M 크기의 빔 형성 행렬이며, k번째 사용자를 위한 빔 형성 벡터 wk는 코드북 wk ∈ {c1c2 ⋯ cQ}에 속하는 코드벡터 중 하나가 선택된다. 코드북 크기 Q=MO는 송신 안테나의 개수 M과 오버샘플링 계수 O의 곱으로 결정되며, 본 논문에서 사용되는 값은 M=12, O=4이다. 벡터 x와 n은 각각 송신 데이터와 가우시안 잡음을 의미한다. 그림 1은 원형 구조의 송신 안테나 어레이를 활용하는 다중 사용자 MIMO 전송 시스템을 나타낸다. 0번째 안테나의 정면 방향인 안테나 기준 송신방향(boresight)과 사용자가 이루는 각도를 사용자 방위각 Φ, m번 째 안테나의 방위각은 Φm=2πm/M으로 정의하며, 이때 m=0,1, ⋯ M−1이다.
Ⅲ. 균일 원형 배열 안테나를 위한 코드벡터
균일 원형 배열 안테나에서 사용하는 코드벡터는 기존의 균일 선형 어레이가 사용하는 이산푸리에변환(DFT) 기반 코드벡터와는 다른 형태이며, 안테나 별 거리차에 따른 채널 위상 보정을 위해 빔포밍 벡터 를 사용한다. 여기서 λ는 반송파 파장의 길이이며 위상 차는 이다[5]. 코드북 C를 구성하는 코드벡터 c는 식 (2)를 활용하여 cq = v|Φ=2πq/Q, q=0,1,…Q−1로 결정된다.
Ⅳ. 점대다점 다중 랭크 빔포밍
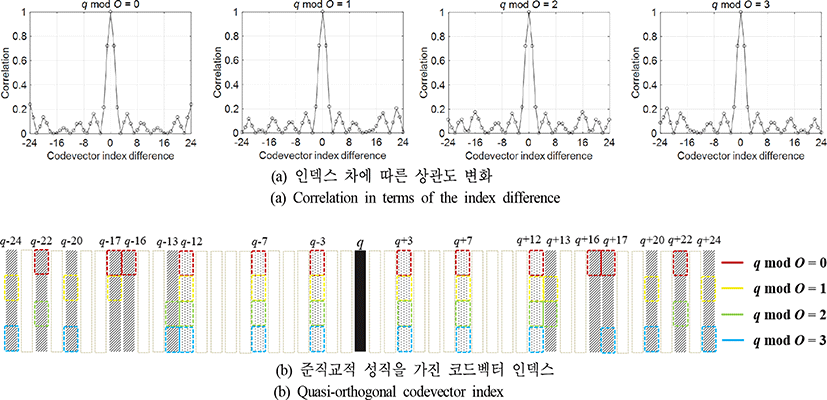
두 코드벡터 cq와 cr의 상관도는 으로 정의되며, μ(q,r)의 값은 0과 1 사이의 값으로 0에 가까울수록 두 코드벡터가 직교성에 근접한다. 고정된 q에 대해 r의 변화에 따른 상관도 그래프를 그림 2에 도시 하였다. q의 변화에 따라 오버샘플링 수 O와 상관도의 패턴 수가 동일하였다. 본 논문에서는 O=4이므로 4개의 규칙이 나타나는데, 이는 q를 4로 나누었을 때 나머지, 즉 mod 함수 값에 따라 규칙이 결정된다.
직교성을 가지는 코드벡터를 찾기 위해 μ(q,r) < x를 만족하는 코드벡터 차 q−r를 표 1에 표시하였다. 상관도의 최댓값은 1이며, 최댓값의 1 %, 0.1 %를 x로 설정하였다. 조건을 만족한 상관도인 q−r를 기재하였고, 공통으로 나타난 것은 χ=1 %일 때 q−r =±3,±7,±12로 총 6개의 코드벡터, χ=0.1 %일 때는 q=r=±3로 2개의 코드벡터가 준직교성을 가지는 것을 확인하였다. x=0.1 %로 설정 시 준직교성을 가지는 코드벡터의 수가 적어 형성할 수 있는 빔 방향에 제한이 있으므로 x=1 %를 기준으로 설정하였다. 그림 2(b)는 x=1 %일 때 각 규칙마다 준직교적 코드벡터를 표시한 그림이다. 빗금 문양은 규칙 중 한번 이상 속한 준직교적인 코드벡터를 표시한 것이고, 점 문양은 공통으로 나타난 준직교적인 코드벡터이다. 또한 이런 준직교적인 코드벡터의 집합을 로 정의한다.
표 1. | Table 1.
준직교적 코드벡터 인덱스 차 | Index difference of quasi-orthogonal codevectors.
|
x |
1% |
0.1% |
|
q mod O=0 |
±3, ±7, ±12, ±16, ±17, ±22 |
±3, ±12, ±17 |
|
q mod O=1 |
±3, ±7, ±12, 13, −17, ±20, 24 |
±3, ±12, −17, 20 |
|
q mod O=2 |
±3, ±7, ±12, ±13, ±22 |
±3 |
|
q mod O=3 |
±3, ±7, ±12, −13, 17, ±20, 24 |
±3, ±12, 17, ±20 |
|
Common |
±3, ±7, ±12 |
±3 |
Download Excel Table
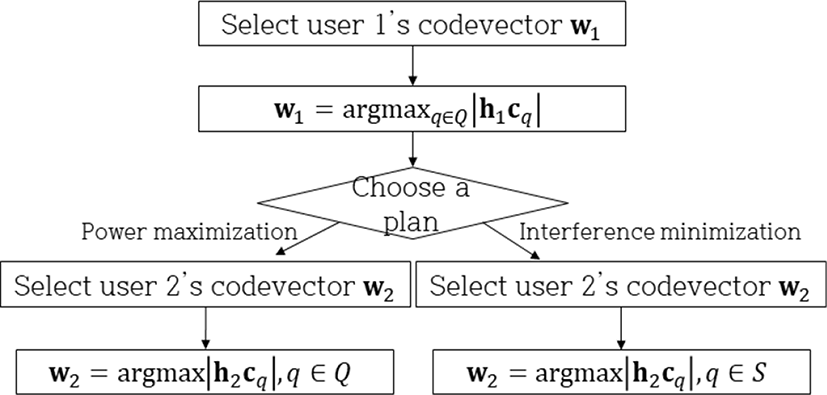
준직교적인 코드벡터를 활용하여 사용자 간 간섭을 최소화하는 알고리듬을 그림 3에 설명하였다. 제안하는 간섭최소화 방식의 비교 대상으로써는 전력 최대화 방식을 활용한다. 순서도에 표시된 바와 같이, 기지국의 스케줄링 방식에 따라 먼저 선택된 사용자를 사용자 1로 정의하고, 사용자 1의 채널 h1과 코드벡터의 상관도를 지표로 최대가 되는 코드벡터 w1를 선택한다. 사용자 2의 코드벡터 w2를 선택하는 방식은 두 알고리듬이 상이하고, 전력 최대화는 w1를 선택하는 방식과 동일하며, 간섭 최소화는 전체 코드북이 아닌 S의 원소인 코드벡터 중 w2를 선택한다. 이 때 S는 q가 w1의 인덱스인 집합이다. 즉, w1과 w2가 준직교적인 빔 쌍이므로 사용자간 간섭이 줄어들어 사용자의 신호 대 간섭 및 잡음비가 증가한다.
Ⅴ. 성능 평가
성능 평가는 단일 안테나를 가진 2명의 사용자에게 동시 전송 시 코드벡터 선택 알고리듬에 따라 성능을 비교하였다. 또한 사용자의 채널은 사용자의 거리 차를 활용 한 기하학적 채널을 활용한다. 사용자 i의 신호 대 간섭 및 잡음비는 이고, 성능지표인 합 전송률은 이다. 표 2는 전체 합 전송률, 사용자 1의 합 전송률, 사용자 2의 합 전송률을 앞서 설명한 방식 별로 비교한 표이다. 전력 최대화 방식 대비 간섭 최소화 방식이 성능이 높은 항목은 전체 합 전송률과 사용자 1의 합 전송률이었고, 각각 약 35.1 %, 95.2 %로 성능 향상이 있다. 반대로 전력 최대화 방식이 성능이 높은 항목은 사용자 2의 합 전송률로 약 39.2 % 높았다. 두 방식을 비교하면 w2의 후보 수가 48개에서 6개로 현저히 줄지만 성능을 높일 수 있다. 동시 전송 사용자의 수가 증가한다면 선택 가능한 빔 쌍의 수가 감소하므로 그에 따라 S를 적절히 활용하는 방안이 필요하다.
표 2. | Table 2.
방식 별 합전송률 | Sum-rate comparison.
|
|
Power maximization |
Interference minimization |
Gain (%) |
|
Sum rate |
10.5 |
14.19 |
35.1 |
|
R
1
|
5.39 |
10.52 |
95.2 |
|
R
2
|
5.11 |
3.67 |
−39.2 |
Download Excel Table
Ⅵ. 결 론
위치가 고정된 사용자에 대해 사용자 간 간섭 제거를 위해 UCA에 적합한 빔을 형성하고, 빔 간 직교성을 활용하였다. 또한 간섭을 최소화하는 방식이 전력을 최대화하는 방식 대비 큰 폭의 성능 이득을 가짐을 확인하였다.
Acknowledgements
본 논문은 한국연구재단 중견연구자지원사업(과제번호 NRF-2017R1A2B4002367) 및 2017년도 연구성과실용화진흥원 기술업그레이드 R&D사업 (과제번호 2017K000348)의 지원으로 수행된 연구 결과임.
References
F. Rusek, D. Persson, B. K. Lau, E. G. Larsson, T. L. Marzetta, and O. Edfors, et al., “Scaling Up MIMO: Opportunities and challenges with very large arrays,”
IEEE Signal Processing Magazine, vol. 30, no. 1, pp. 40-60, Jan. 2013.


Y. Zeng, R. Zhang, “Millimeter wave MIMO with lens antenna array: A new path division multiplexing paradigm,”
IEEE Transactions on Communications, vol. 64, no. 4, pp. 1557-1571, Apr. 2016.


T. A. Thomas, F. W. Vook, “Improving the performance of the UCA when using LTE codebook feedback,” in
2012 IEEE Wireless Communications and Networking Conference(WCNC), Shanghai, Apr. 2012, pp. 847-851.


L. Wu, H. Yang, and D. Wang, “Hadamard transform based codebook design for uniform circular arrays in mobile radio communications,” in
2012 IEEE Vehicular Technology Conference(VTC Fall), Quebec City, Sep. 2012, pp. 1-5.


L. Zhou, Y. Ohashi, “Performance analysis of mmWave LOS-MIMO systems with uniform circular arrays,” in
2015 IEEE 81st Vehicular Technology Conference(VTC Spring), Glasgow, 2015, pp. 1-5.