Ⅰ. 서 론
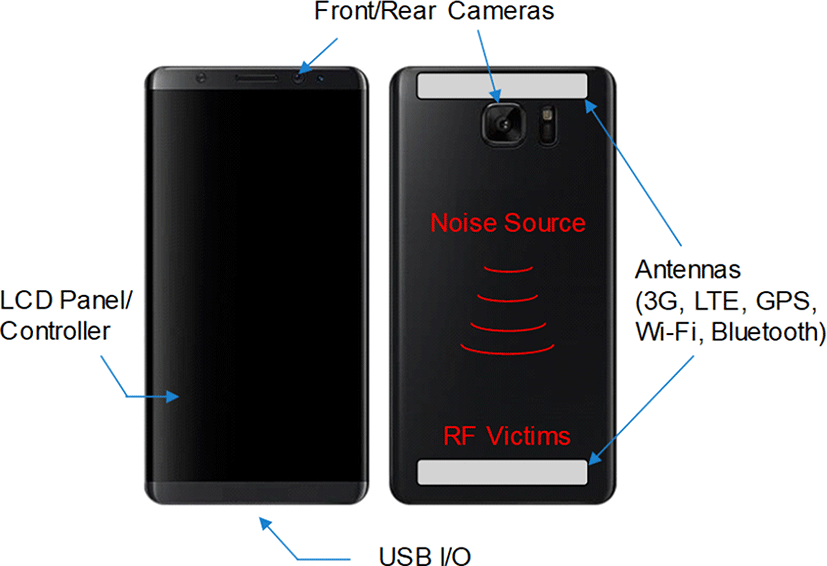
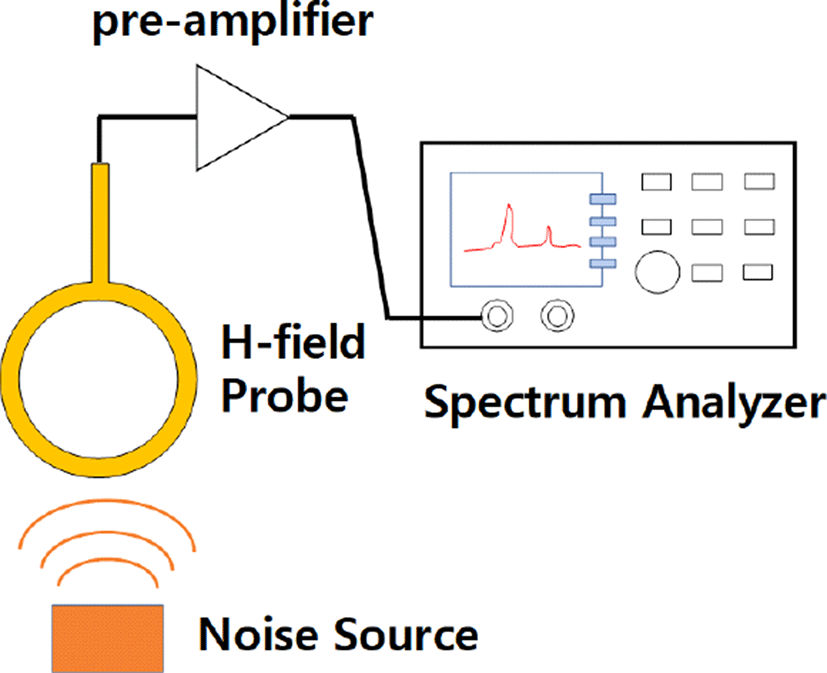
최근 모바일 무선기기는 소형화, 박형화 및 다기능화됨에 따라 시스템의 집적도가 증가하고 있다. 집적도가 증가함에 따라 시스템 내부의 여러 디지털/RF 모듈 및 센서 등 내부 부품들이 매우 근접하게 배치되며, 이에 따라 디지털 부품의 고속 스위칭 노이즈로부터 발생된 전자파가 시스템 내부 안테나에 간섭을 일으키는 Radio-Frequency Interference(RFI) 문제가 대두되고 있다[1]. 그림 1은 모바일 기기 내 RFI 간섭 메커니즘을 보여주고 있다. 모바일 기기 내에 있는 카메라 모듈, LCD 모듈, I/O 등의 클럭 주파수 혹은 고조파 성분으로 방사된 전자파가 GSM, GPS, Wi-Fi 등 통신 대역의 안테나에 간섭이 되며, 그 결과로 비트 오류율(Bit Error Rate: BER) 증가를 야기하여 무선 통신 대역의 수신감도 저하로 이어지게 된다. 이런 RFI 간섭 현상에 대한 분석 및 대응설계를 위해서는 RFI 노이즈 원을 특정하기 위한 측정 기술의 연구가 중요하다. RFI 노이즈 원을 측정하는 방법은 여러 가지가 있으며, 코일 형태의 자기장 프로브를 이용한 측정 방법이 널리 사용되고 있다[2]. 자기장 프로브는 패러데이법칙에 기반하여 근접장(near-field) 영역의 시변하는 자기장에 의해 프로브 코일에 유도되는 전류를 감지하게 되며, 일반적인 측정 셋업은 그림 2와 같다. 노이즈 원으로부터 방사된 자기장이 코일 형태의 프로브에 감지되고, pre-amplifier 를 통해 증폭되어 spectrum analyzer로 측정된다.
RFI 측정에 사용되는 프로브는 일반적으로 표면이 절연된 전선을 기구적으로 감아 제작된다. 그러나 기구적 제작과정의 태생적 한계로 인하여 정밀성, 재현성, 내구성 등의 한계를 가진다. 이를 보안하기 위해 최근 Printed Circuit Board(PCB) 상에 인쇄된 형태의 프로브인 Printed Spiral Coil(PSC)이 많이 사용되며 기존 연구를 통해 모델링이 진행되었다. 그러나 기존 PSC 모델은 L/C 집중 소자(lumped element) 기반의 간단한 구조로 인하여 고주파 정확성이 부족하며, 따라서 최근 무선 통신 대역이 높아져감에 따른 기가헤르츠(GHz) 영역의 RFI 노이즈 원 측정용으로 활용하기에 한계가 있다[3]. 본 논문에서는 기존 모델의 한계를 개선하기 위한 PSC의 고주파 모델을 새로이 제안하였다. 제안된 모델은 고주파 정합성을 확보하기 위하여 PSC의 설계변수에 기반한 분포 모델(distributed model)로 설계되었으며, 제안된 분포 등가회로 모델을 바탕으로 T-pi 등가변환을 이용한 PSC의 자기 임피던스(self-impedance)의 해석적 모델(analytic model) 역시 새로이 제안되었다. 제안된 모델의 실제 고주파 RFI 측정 시 효용성을 확인하기 위하여, 임의의 RFI 노이즈 원으로 설계된 마이크로스트립 라인과 PSC 사이의 전달함수(transfer function)를 제안된 모델과 상호 인덕턴스(mutual inductance)를 결합하여 추출하였다. 제안된 PSC 모델의 자기 임피던스와 전달함수는 3D field solver를 이용한 시뮬레이션 및 실 측정으로 6 GHz까지 높은 정합성과 함께 검증되었다.
Ⅱ. PSC의 고주파 모델링
본 장에서는 PSC의 고주파 모델링을 위해 설계변수에 기반한 분포 모델과 자기 임피던스 분석을 위한 해석적 모델이 제안되었다. 분포 모델은 각 등가회로 성분이 여러 segment로 나뉘어져 구성되는 모델이다. 분포 모델은 선로 위치에 따른 전류의 크기와 위상의 변화를 잘 표현할 수 있으므로, 파장이 선로 길이에 비해 짧아지게 되는 고주파 영역의 모델링에 적합하다. 또한 제안된 모델의 RFI를 측정하는 프로브로서의 효용성을 확인하기 위한 전달함수 등가회로 모델이 제안된다.
PSC는 기판 위의 동일 평면상에 도전성 선로가 여러 턴으로 회귀하는 구조로 설계된다. 그림 3은 PSC의 구조 및 설계변수를 보여주고 있다. PSC는 라인의 넓이(w), 라인 사이의 거리(s), 사각형일 경우 한 변의 외곽 길이(do), 턴 수(N) 총 네 개의 설계변수를 가지고 있다. 또한 설계변수에 의해 결정되는 등가 회로 성분으로 라인 자체에 존재하는 자기 인덕턴스(self-inductance)와 라인 사이에 존재하는 상호 인덕턴스(mutual inductance), 커패시턴스(capacitance)가 있다.
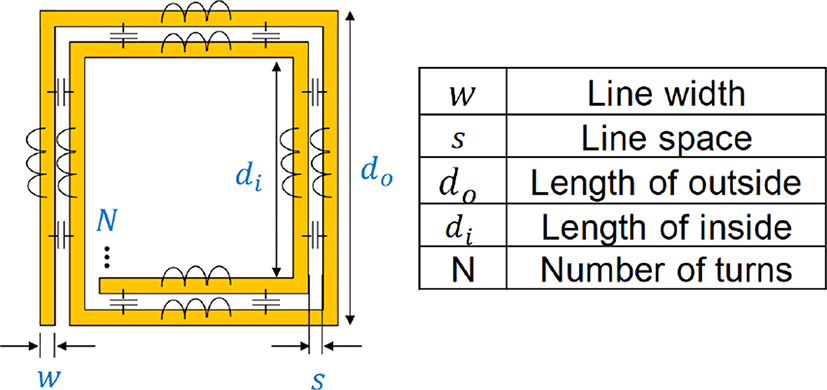
그림 4는 n개의 segment로 분포되어 있는 PSC의 분포 모델을 보여주고 있다. 등가회로 상에서 자기 인덕턴스는 각 턴의 라인을 따라 모델링되었으며, 한 턴이 끝나고 다음 턴으로 회귀하는 코일의 특성에 따라 외곽 라인의 종단과 내곽 라인의 초단이 사선으로 연결되었다. 상호 인덕턴스와 상호 커패시턴스는 라인 사이에 존재하는 성분이므로 자기 인덕턴스 사이에 구성되었다. 자기 인덕턴스와 상호 인덕턴스는 n으로, 커패시턴스는 등가회로의 상호성(reciprocity) 특성을 나타내기 위해 n+1로 등분되었다. Segment의 개수 n은 식 (1)과 식 (2)에 따라 각 segment가 모델링 최대 주파수(fmax)에 해당하는 한 파장(λ)의 20 등분 길이가 되도록 결정되었다.
fmax: 모델링 최대 주파수
ltotal: 선로 전체 길이
식 (3)은 설계변수에 기초한 자기 인덕턴스 모델(L)을 나타낸다[4].
N은 PSC의 턴 수, μ=μrμ0는 투자율(permeability), davg=(do+di)/2는 외곽 라인의 길이 do와, do, w, s, n으로 표현되는 내곽 라인의 길이 di의 평균값으로 결정된다. Φ=(do−di)/(do+di)는 fill factor로서, PSC가 외곽 둘레 부분에만 감겨있을 경우인 0부터, 중심까지 감겨 있을 경우인 1까지 바뀌는 설계변수이다. 또한 식 (4)는 각 턴 사이에 존재하는 상호 인덕턴스 모델(M)을 나타낸다[5].
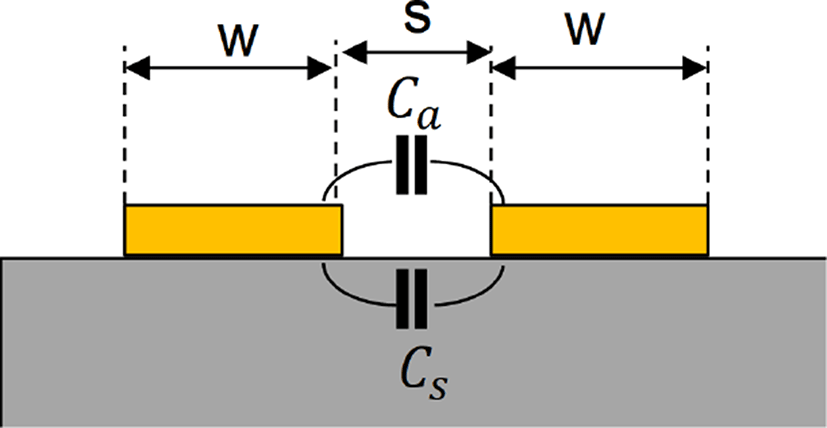
커패시턴스는 동일 평면상에 존재하는 라인인 coplanar line 사이의 커패시턴스 모델이 차용되었다. 그림 5는 coplanar line의 구조를 보여주고 있다. 커패시턴스는 라인의 폭 w와 라인 사이의 거리 s에 의해 결정되며, 라인의 두께가 0이고, 기판의 두께가 무한할 때 공기 영역을 통과하는 커패시턴스 Ca와 유전체 영역을 통과하는 커패시턴스 Cs의 합으로 구할 수 있다. 그러나 기존 coplanar line의 커패시턴스 모델은 fringing effect가 고려되지 않은 마주보는 두 도체판으로부터 등각 사상(conformal mapping) 기법을 이용하여 추출되었기 때문에 fringing effect가 큰 폭이 얇은 구조의 라인에서 정확성이 떨어지고, 이를 개선하기 위해 fringing effect가 고려된 마주 보는 두 도체판 사이의 커패시턴스 모델로부터 추출되었다. 식 (5)는 공기 중에서의 fringing effect가 고려된 두 도체판 사이의 단위 길이 당 커패시턴스 모델(C)을 나타낸다[6].
여기서 R=K(k′)/K(k), K는 제1종 타원 적분 (complete elliptic integral of the first kind)이며, k와 k′은 식 (6)에 의해 결정된다.
라인이 유전율 εr을 가진 유전체 내부에 있을 경우의 커패시턴스는 식 (5)의 결과에 유전율 εr의 곱으로 표현할 수 있다. 본 논문의 PSC는 한 쪽 공간에만 유전체가 존재하는 구조이므로 유전체 내부에 있을 경우와 공기 중에 있을 경우의 평균인 (εr+1)/2의 곱으로 표현할 수 있다. 단, 이는 유전체 두께가 무한하다고 가정했을 경우이며, 기판 두께가 라인 사이의 거리 s의 2배 이상일 때 높은 정확성을 가진다[7].
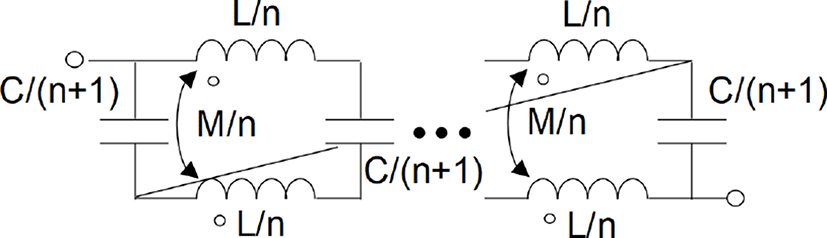
앞 절에서는 PSC의 등가회로가 제안되었다. 그러나 설계변수와 검증 주파수 범위가 달라질 때마다 등가회로를 다시 구성해야 하는 한계가 있으므로 등가회로에 대한 해석적 모델을 추가적으로 제안하였다. 그림 6은 T-Pi 변환 및 역변환을 적용하여 제안된 등가회로 모델의 segment 개수를 줄여 해석적 모델이 용이하도록 간략화 하는 과정을 보여주고 있다. 등가회로 성분 Ls와 Ms는 segment 개수 n으로, 그리고 Cs는 n+1로 등분된 자기 인덕턴스와 상호 인덕턴스, 그리고 커패시턴스이다. 그림 6(a)의 PSC 등가회로 상에서 상호 인덕턴스를 직접 계산하기가 어려우므로 그림 6(b)와 같이 상호 인덕턴스가 포함된 등가 평형(balanced) T형 모델로 변환한다. 그림 6(c)는 T-Pi 등가 변환을 적용하여 pi형 모델로 변환된 모습을 보여주고 있다. 그림 6(d)는 pi형 모델 종단에 있는 Za와 커패시턴스를 하나의 임피던스로 간주하여 그림 6(c)의 역변환인 Pi-T 등가 변환을 적용한 것을 보여주고 있다. 그림 6에서 보인 과정에 따라 등가회로의 한 개의 segment 개수가 줄어들게 된다. 따라서 변환된 회로 중앙 임피던스 Z3와 종단의 인덕턴스들을 그림 6(a)에 표현된 변환 전 임피던스로 간주하여 위 과정을 반복하면 n개 segment로 구성된 등가회로 모델을 1개의 Pi형 모델로 표현이 가능하며 병렬 덧셈 식을 통해 자기 임피던스의 해석적 모델을 추출할 수 있다.
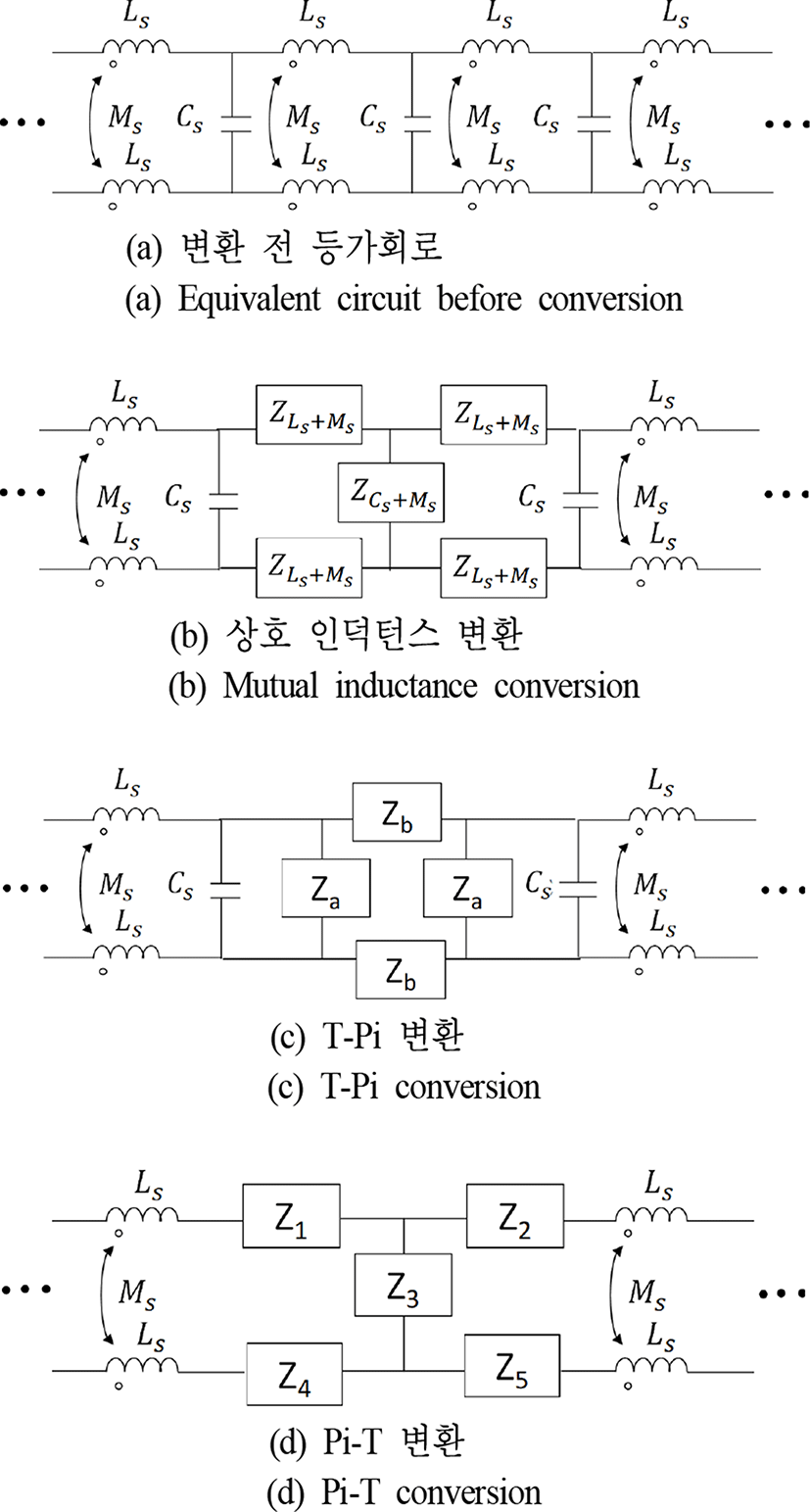
그림 7은 등가회로의 변환 과정 중 상호 인덕턴스의 등가 변환을 보여주고 있다. 그림 7(a)와 7(b)가 서로 회로적으로 등가이려면 port 1의 전압 V1과 port 2의 전압 V2가 동일해야 한다. 그림 7(a) 회로의 port 1 전압 Va1과 port 2의 전압 Va2, 그리고 그림 7(b) 회로의 port 1 전압 Vb1과 port 2의 전압 Vb2는 각각 식 (7)~(9)과 같다.
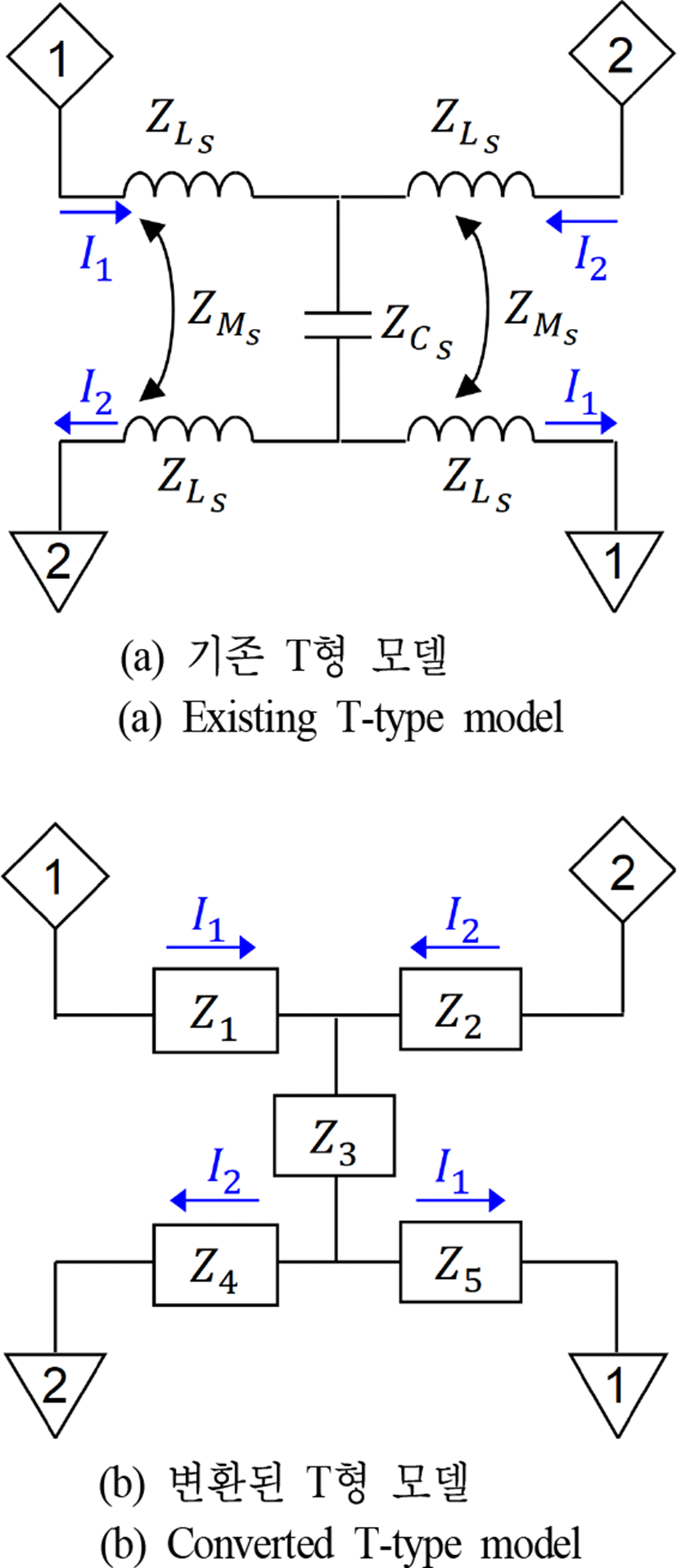
제안된 회로의 인덕턴스들은 segment 개수로 등분되었기 때문에 각 segment의 직렬 인덕턴스의 임피던스(Z1, Z2, Z4, Z5)가 동일하므로, 식 (7)과 식 (8), 그리고 식 (7)과 식 (9)가 등가일 때 방정식의 해 Z1, Z2, Z3, Z4, Z5는 각각 식 (10) 및 식 (11)과 같다.
그림 8은 등가회로의 변환 과정 중 T-Pi 등가 변환을 보여주고 있다. 그림 8(a)와 그림 8(b)의 회로가 등가이기 위해서는 서로 동일한 Z-parameter를 가져야 한다. T형 모델과 Pi형 모델 각각의 Z-parameter는 표 1에 정리되었다. T-Pi 변환을 위해서 각 모델의 자기 임피던스와 전달임피던스(transfer impedance)가 서로 등가가 되어야 하며, 식 (12) 및 식 (13)은 각 segment의 병렬 커패시턴스의 임피던스(Za, Zb)와 직렬 인덕턴스의 임피던스(Zc, Zd)가 동일할 때 등가변환 식을 나타낸다.
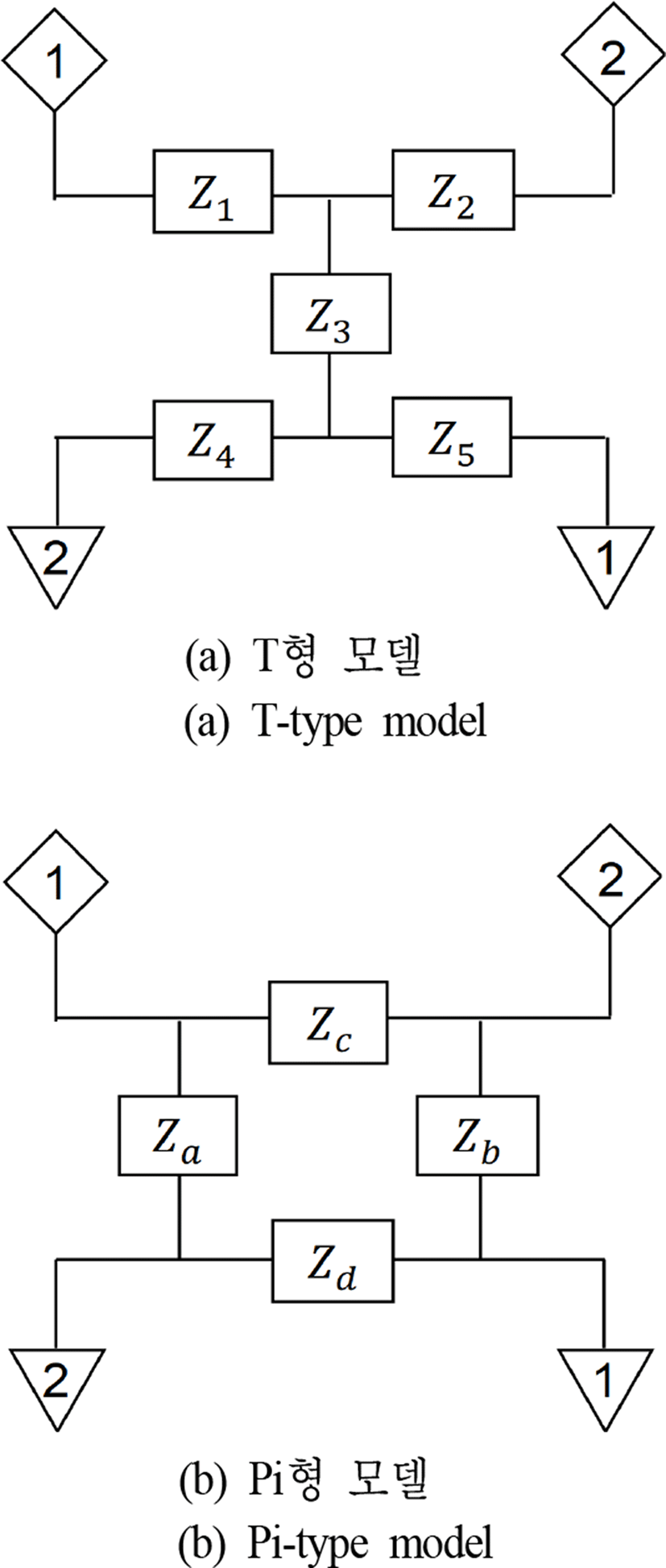
| Z-parameter | T model | Pi model |
|---|---|---|
| Z 11 | Z1 + Z3 + Z5 | |
| Z12 = Z21 | Z 3 | |
| Z 22 | Z1 + Z3 + Z4 |
식 (10), 식 (11)을 식 (12), 식 (13)에 대입함으로써 그림 6에서 소개한 PSC 등가회로의 변환 과정을 수행할 수 있다. 위 과정을 반복적으로 수행함으로써 n개의 segment를 가지는 PSC 등가회로 모델을 1개의 pi형 모델로 변환할 수 있고, 변환된 모델로부터 PSC의 자기 임피던스에 대한 해석적 모델은 식 (14)와 같이 표현되며, 각 계수 값은 표 2에 정리되었다.
| Coefficient | Impedance |
|---|---|
| α | |
| β | |
| γ | |
| A 1 | |
| P | 2(ZL−ZM)+ZC |
| q | 2ZC(ZL−ZM) |
| r | Z C |
| 2(ZL−ZM+ZC) | |
| 2(ZL+ZM) |
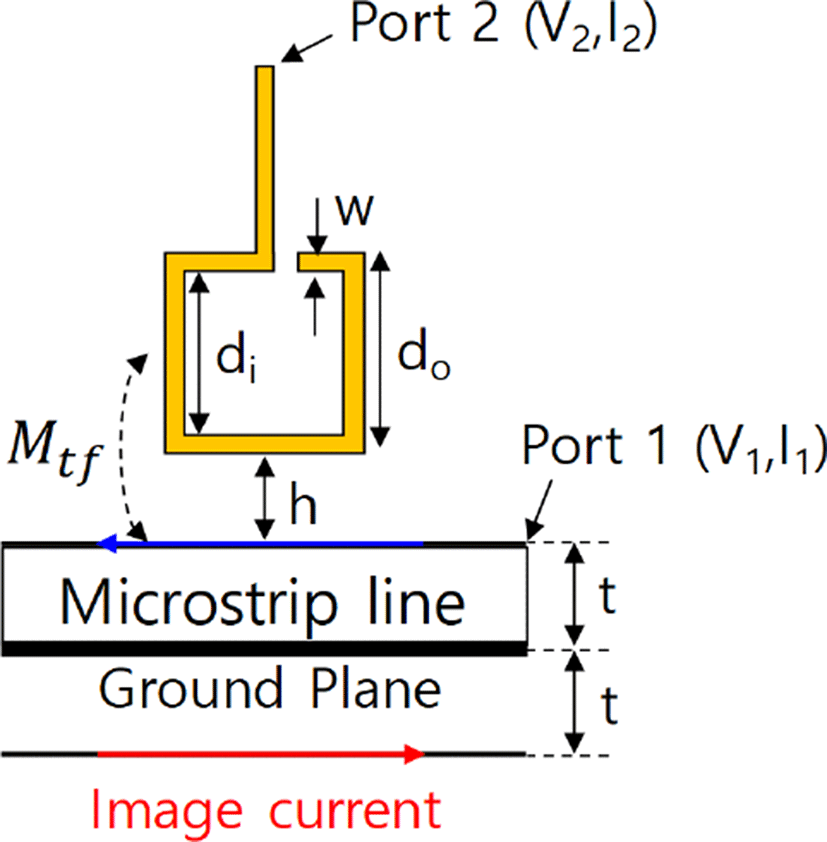
앞 절에서는 PSC의 분포 모델을 사용한 고주파 등가회로 모델 및 해석적 모델이 제안되었다. 본 절에서는 PSC의 RFI 노이즈 원을 측정하는 프로브로서 효용성을 확인하기 위하여, 앞서 제안된 PSC 모델을 이용하여 RFI 노이즈의 전달함수 모델을 제안한다. 그림 9는 RFI 노이즈 원으로 가정된 마이크로스트립 라인(microstrip line)과 PSC의 모습을 보여주고 있다. 마이크로스트립 라인과 PSC는 자기적 결합을 형성하고 있으며, 그에 따른 상호 인덕턴스 Mtf 모델은 식 (15)에서 확인할 수 있다[8].
그림 10은 전달함수 모델링을 위한 등가회로 모델을 보여주고 있다. 상호 인덕턴스 Mtf로 자기적 결합을 하고 있는 마이크로스트립 라인과 PSC 사이의 전달함수에 대 한 등가모델이 그림 10(a)에 제시되어있으며, 과 은 1개의 pi 모델로 수렴된 PSC 등가회로의 인덕턴스와 커패시턴스의 임피던스이다. 그림 10(b)는 상호 인덕턴스에 의해 유도되는 전압 Vind를 전원 소스로 표현한 등가회로를 보여주고 있다. 상호 인덕턴스가 Mtf이고 마이크로스트립 라인에 흐르는 전류가 I1일 때 유기되는 전압은 Vind=jωMtfI1으로 표현 될 수 있으며 이 때 PSC와 마이크로스트립 라인 사이의 전달 임피던스 (Z21) 는 식 (16)과 같이 표현된다.
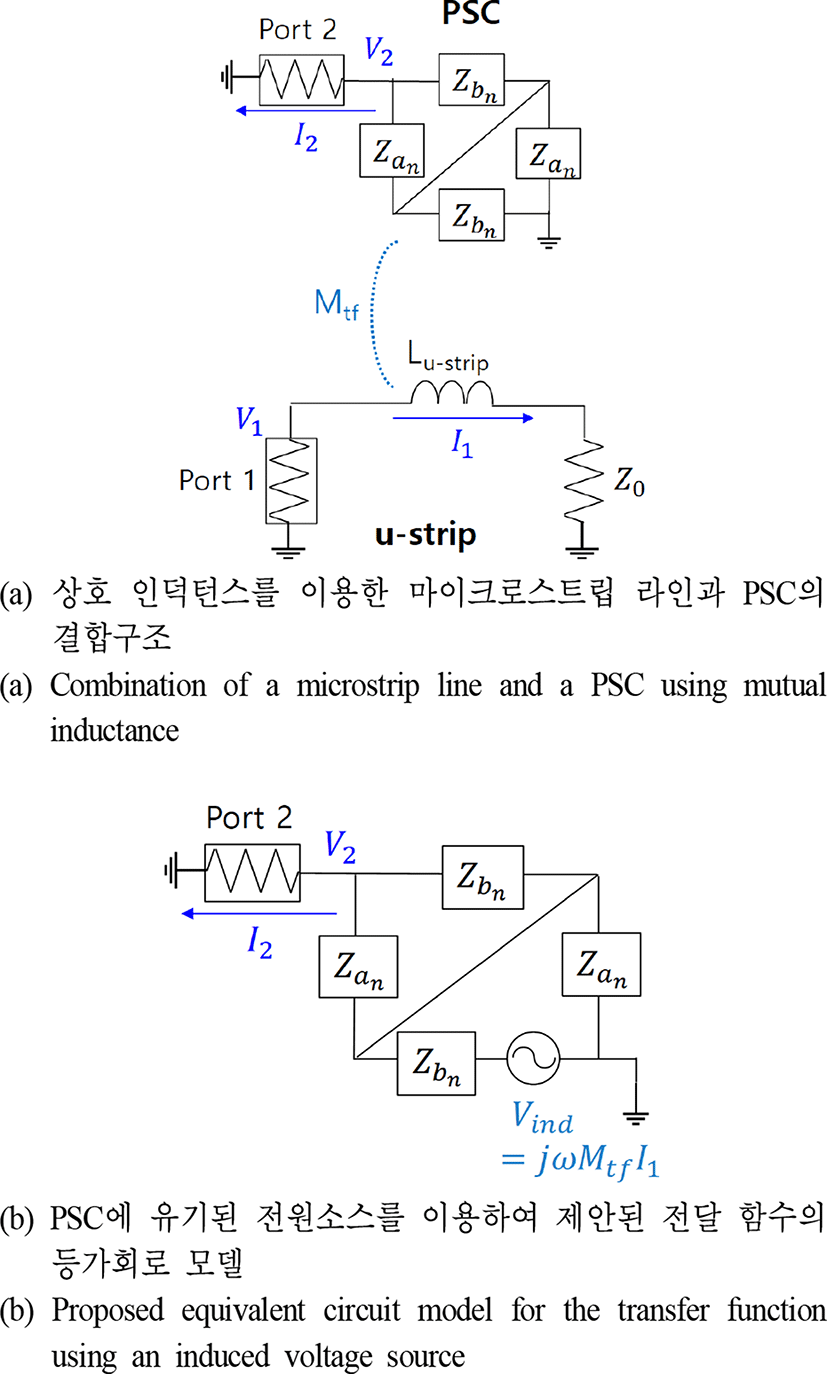
Z-parameter의 정의에 의해 I2=0일 경우 port 2와 인접한 임피던스 과 이 무시될 때 전압 분배 법칙에 의해 으로 표현된다. 식 (16)과 앞 절에서 제안된 PSC의 해석적 모델인 식 (14)를 결합하여 도출된 전달 임피던스의 모델은 식 (17)과 같다. 앞 절에서 제안된 PSC의 자기 임피던스 모델과 전달함수 모델을 이용하여, S-parameter와 Z-parameter의 변환 식에 기반한 최종 전달함수(S21)를 식 (18)과 같이 추출할 수 있다[9].
Ⅲ. 시뮬레이션 및 측정 검증
제안된 PSC의 임피던스와 전달함수 모델을 검증하기 위한 시뮬레이션 및 측정을 수행하고 모델과 비교하였다. RFI 노이즈 원으로서 그림 11과 같이 50 Ω으로 설계된 마이크로스트립 라인을 사용하였으며, 전체 크기 100 mm × 50 mm, 두께 1.6 mm의 FR4 기판 위에 신호선 폭 3.4 mm 로 설계되었으며, 임피던스 매칭을 위해 신호가 인가되는 포트의 반대편을 50 Ω 종단(termination) 처리하였다.
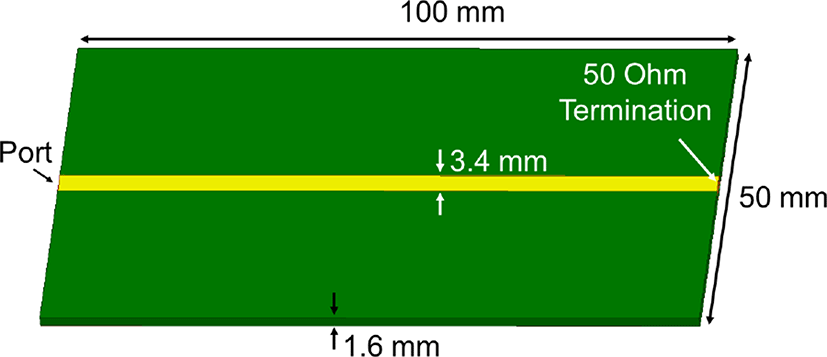
그림 12와 그림 13은 각각 제안된 임피던스와 전달함수 모델을 검증하기 위한 3-dimensional field simulation 구조와 Vector Network Analyzer(VNA)를 이용한 측정셋업을 보여주고 있다. 마이크로스트립 라인 상부에 라인과 평행한 방향으로 하여 PSC의 하단 부분과 라인사이의 거리(h)를 3.5 mm 만큼 이격시켰다. 시뮬레이션과 측정 모두 1 MHz~6 GHz의 주파수 범위로 하여 port 1에서의 자기 임피던스(Z11) 및 port 1과 port 2 사이의 전달함수 (S21) 을 대상으로 수행되었다. 시뮬레이션 및 측정 검증에 사용된 PSC는 1.6 mm 두께의 FR4 기판 위에 설계변수 w=0.1 mm, s=0.1 mm, do=20 mm, N=2로 제작되었다.
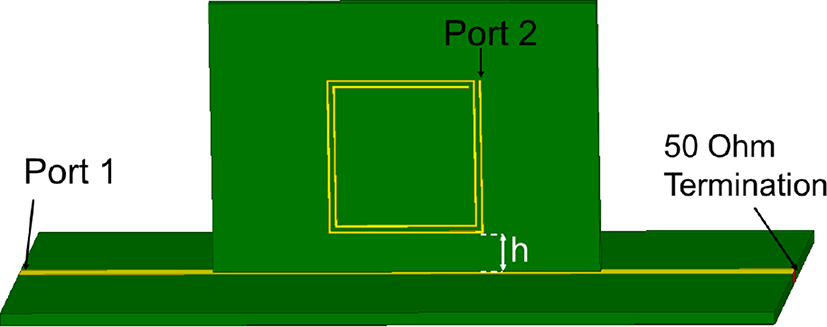

그림 14는 3D field simulation을 통한 제안된 PSC의 자기 임피던스의 고주파 검증 결과를 보여주고 있다. 집중 소자 회로의 경우 약 250 MHz 대역에서 자기 인덕턴스와 선로 간의 기생 커패시턴스에 의한 병렬 공진 이외 1 GHz 이상의 고주파 영역에서의 정합성이 보장이 되지 않는 것을 확인할 수 있다. 반면에 분포 모델의 경우, 파장에 따라 발생되는 partial 성분에 의한 고주파 직렬 및 병렬 공진들을 확인할 수 있다.
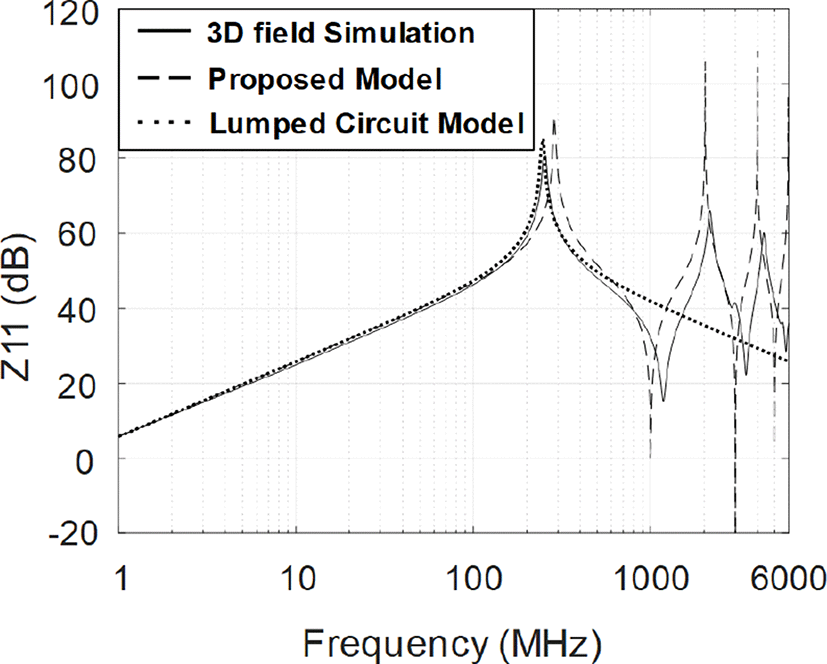
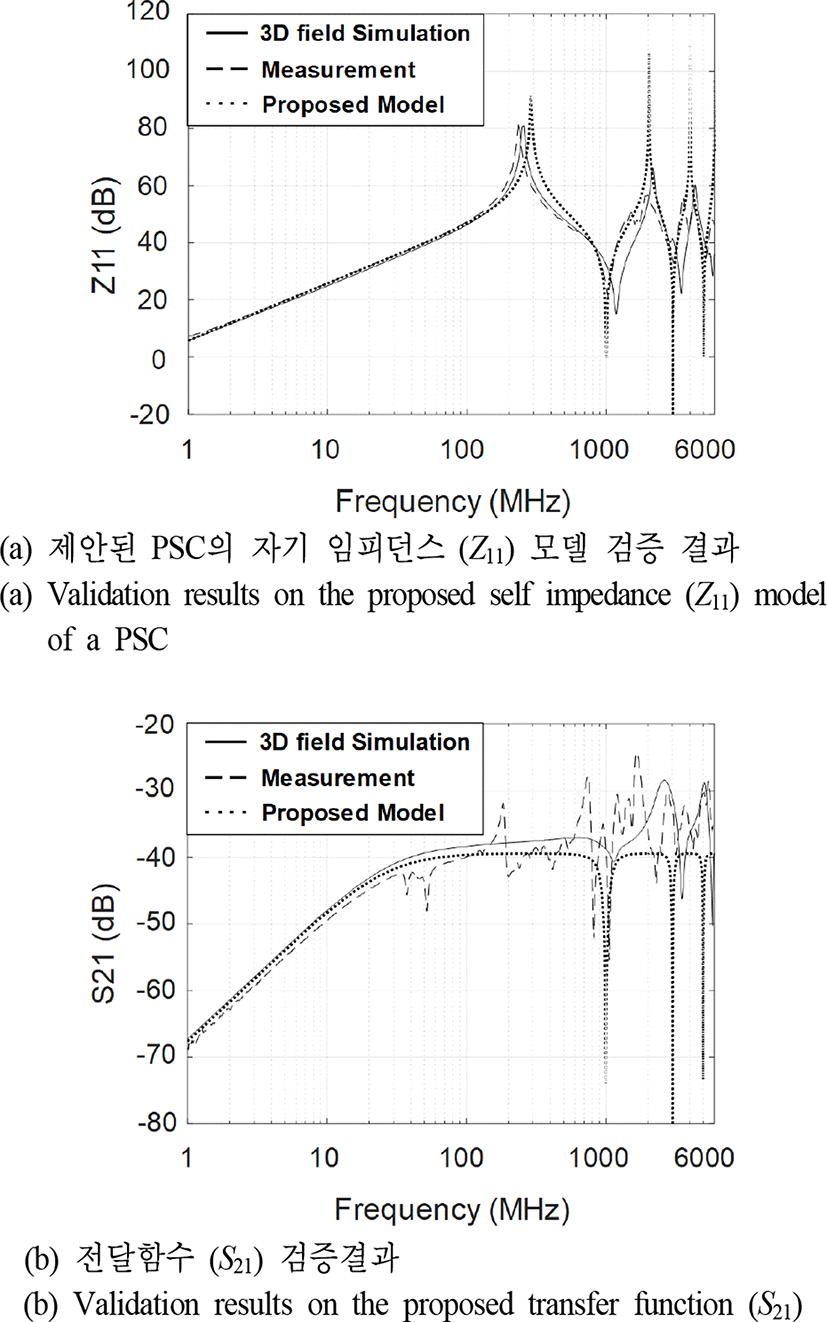
그림 15(a)는 제안된 PSC의 자기 임피던스 모델의 시뮬레이션 및 측정 검증 결과를 보여주고 있다. 공진 주파수를 기준으로 시뮬레이션, 계산, 측정 결과가 전 대역에서 높은 정합성을 보임을 확인하였다. 그림 15(b)는 제안된 PSC 모델을 바탕으로 추출한 전달함수의 시뮬레이션 및 측정 검증 결과를 보여주고 있다. 등가회로 모델의 경우 저항 성분을 고려하지 않아 높은 공진이 발생하며 측정 결과의 경우 방송 및 통신대역 신호의 간섭으로 인한 외부 노이즈 성분의 영향이 포함되었으나, 이를 제외하면 제안된 전달함수 모델이 전 주파수 대역에서 2 dB 이하의 오차와 함께 시뮬레이션 및 측정 결과와 높은 정합성을 보임을 확인하였다.
Ⅳ. 결 론
본 논문에서는 기존 집중 소자로 구성된 기존 PSC 프로브 모델의 유효 대역폭 한계를 개선하기 위하여, 고주파 분포 모델 및 해석적 모델을 새로이 제안하였다. 제안된 모델은 3D field solver를 이용한 시뮬레이션 및 VNA를 이용한 측정으로 검증되었다. 제안된 PSC의 자기 임피던스 모델이 6 GHz까지의 고주파 대역에서 시뮬레이션 및 측정결과와 높은 정합성을 보임을 확인하였다. 또한 제안된 모델의 고주파 RFI 측정 시 효용성을 검증하기 위하여, 임의의 RFI 노이즈 원으로 설계된 마이크로스트립 라인과 PSC 사이의 전달함수를 제안된 임피던스 모델을 기반으로 추출하였다. 전달함수 역시 저항 성분의 부재와 외부 노이즈 성분을 제외했을 때 전 주파수 대역에서 시뮬레이션 및 측정결과 대비 2 dB 이하의 높은 정합성으로 검증되었다. 제안된 PSC의 자기 임피던스 및 전달함수 모델은 기가헤르츠(GHz) 영역의 고주파 통신대역에서의 RFI 측정용 프로브 설계 및 노이즈 간섭 예측 등에 효율적으로 활용될 것으로 사료된다.